Following this youtube link:https://www.youtube.com/watch?v=UzxYlbK2c7E&list=PLA89DCFA6ADACE599

Machine Learning, in essence, is “the field of study that gives computers the ability to learn without being explicitly programmed” per Arthur Samuel stated in 1959.

Outline of the full 20 courses:
1 an overview of the course in this introductory meeting.
2 linear regression, gradient descent, and normal equations and discusses how they relate to machine learning.
3 locally weighted regression, probabilistic interpretation and logistic regression and how it relates to machine learning.
4 Newton’s method, exponential families, and generalized linear models and how they relate to machine learning. Note Newton’s method is an iterative numerical optimization technique used to find the roots of a function or optimize convex functions. It is particularly useful in convex optimization problems like logistic regression. It utilizes not only first derivative, i.e. gradient descent or Jacobian matrix but second derivative hessian matrix.
5 generative learning algorithms and Gaussian discriminative analysis and their applications in machine learning. Note generative first Generalize P(X|Y), then obtain P(Y|X), X is evidence Y is prediction, while
6 naive Bayes, neural networks, and support vector machine.
7 optimal margin classifiers, KKT conditions, and SUM duals.
8 support vector machines, SVM, including soft margin optimization and kernels.
9 learning theory, covering bias, variance, empirical risk minimization, union bound and Hoeffding’s inequalities.
10 learning theory by discussing VC dimension and model selection.
11 Bayesian statistics, regularization, digression-online learning, and the applications of machine learning algorithms.
12 unsupervised learning in the context of clustering, Jensen’s inequality, mixture of Gaussians, and expectation-maximization.
13 expectation-maximization in the context of the mixture of Gaussian and naive Bayes models, as well as factor analysis and digression.
14 factor analysis and expectation-maximization steps, and continues on to discuss principal component analysis (PCA).
15 principal component analysis (PCA) and independent component analysis (ICA) in relation to unsupervised machine learning.
16 reinforcement learning, focusing particularly on MDPs, value functions, and policy and value iteration.
17 reinforcement learning, focusing particularly on continuous state MDPs, discretization, and policy and value iterations.
18 state action rewards, linear dynamical systems in the context of linear quadratic regulation, models, and the Riccati equation, and finite horizon MDPs.
19 debugging process, linear quadratic regulation, Kalmer filters, and linear quadratic Gaussian in the context of reinforcement learning.
20 POMDPs, policy search, and Pegasus in the context of reinforcement learning.

Supervised learning: two types, one is directly judging the probability, while the other is Bayes probability model.

Above lecture was posted on 2008, he released a newer one in 2016, the Synopsis are:

1.0 introduction
2.0 linear regression
3.0 linear algebra
4.0 linear regression
5.0 octave tutorial
6.0 logistic regression
7.0 regularization
8.0 neural networks
9.0 neural networks learning
10.0 adice for applying machine learning
11.0 machine learning system design
12.0 support vector machines SVM
13.0 clustering
14.0 dimensionality reduction
15.0 anomaly detection problem
16.0 recommendation system
17.0 large scale machine learning
18.0 application example
19.0 conclusion

The key theory is to minimize the cost function composed of m samples labeled with n features (in matrix form), and gradient descent is used to construct this cost function. However, Professor Ng first described “normal equations” as

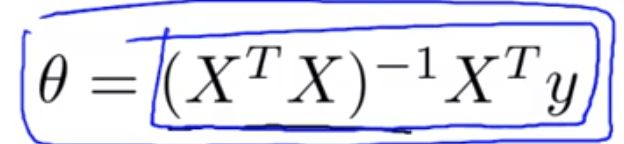
More detailed explanation from AI was added in Fed 2025:

So use normal equation is a great alternative to solve theta, however, when the feature numbers goes large, i.e. 2000, it’s optimal to use gradient descent.

The major topic covered are