According to the wiki, “Laplace Transform” transforms a function of a real variable t (often time) to a function of a complex variables (complex frequency). The transform has many applications in science and engineering.

It’s similar to Fourier transform with a difference that Fourier transform of a function is a complex function of a real variable, while the Laplace transform of a function is a complex function of a complex variable.

Then what is Laplace Transform, and of course, an alternate notation for the Laplace transform is 

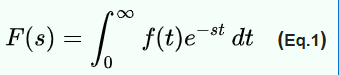
Right from the beginning, we need to know why mathematicians such as Lagrange, Laplace, Fourier would come up with all sorts of “transforms”, simple, they just want to solve differential equations after Newton and Leibniz invented calculus. It’s not easy to solve these Differential Equations(DEs).

So Laplace come up with this Laplace Transforms, and painstakingly built up a table of Laplace equations. For example, to solve this DE:

Established tables find (all proved) that

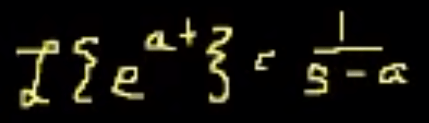
It’s eventually solved as (per Khan Academy)

Another example is provided by this math tutor,

To sum, the table of some Laplace transforms are:

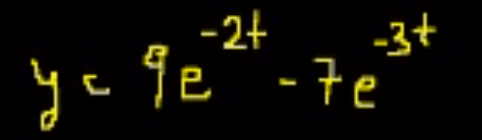
Now let’s get into more hairy territory, note the bottom equation is the original form, while the top one is deduced thanks to the bridge aid in the middle.

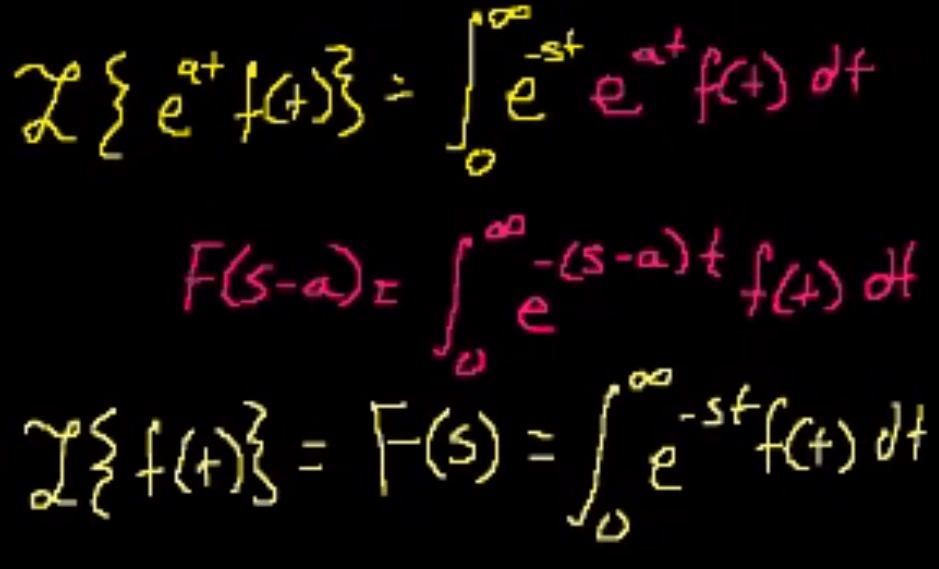
And the crux is that s represents frequency domain while t is the time domain, sounds familiar to Fourier transform, right?

In the application of physics, wiki provides an example of how Laplace transform helps to solve the radioactivity decay equation.

If we can solve this DE to get a normal function to time t, so we can predict what’s the radioactive metric after certain time.

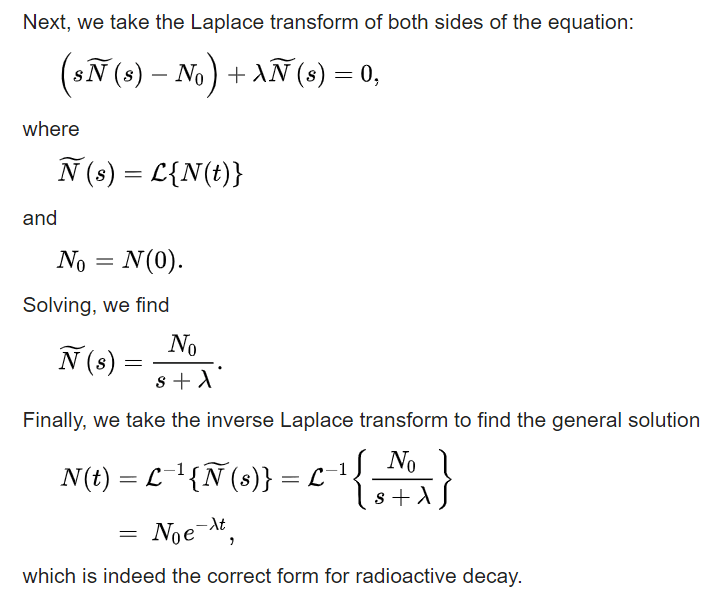
On Dec 10th, 2021, my understanding of Laplace and Fourier Transform reached a new level. Thanks to Dr.Steve Brunton, I learn that the Laplace transform is a culmination or generalized version of Fourier Transform. Fourier transform only allows real number for w, frequency, while Laplace allows complex sigma + iw, it’s more general!

As shown below, Fourier Transform has its limitation, so the ingenuity of Laplace is to compose f(t) with an exponentially decay function and heavy-sided function together,

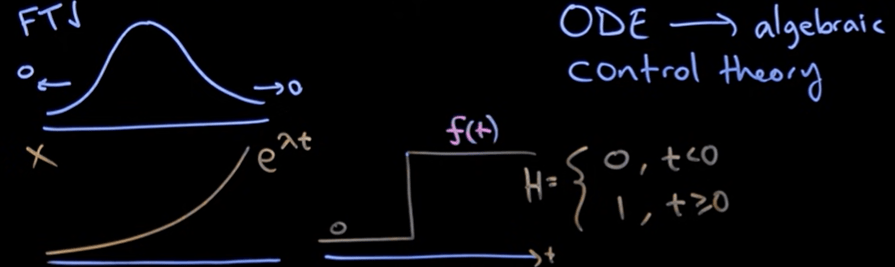
so a normal Fourier Transform F hat in w variable can be expressed as below:

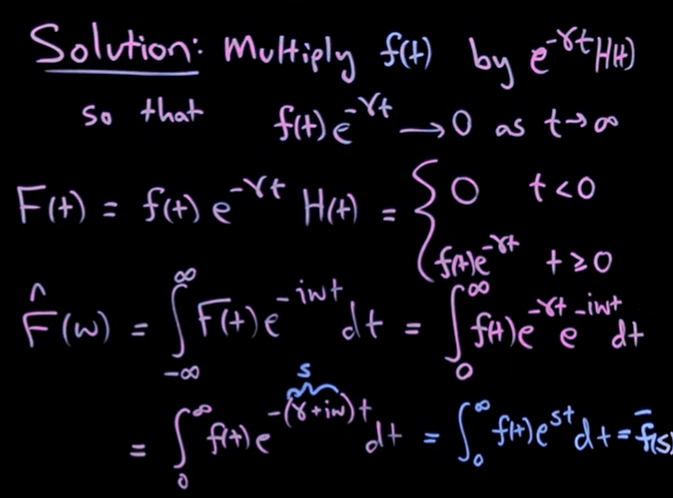
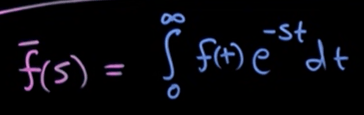
And the inverse Laplace Transform is