Fourier Transform is highly regarded for its impact in advancing modern technology, while its format nevertheless looks quite similar to Laplace Transform. Let’s take a look:

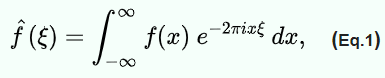
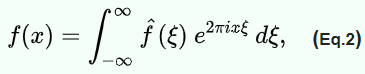
Recall from the last blog, I re-pasted the Laplace Transform below:

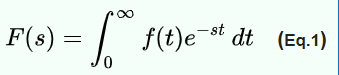
Laplace transform, from my view, seems to help solve abstract DE as a powerful tool, while Fourier Transform is more related to its extensive application in technologies such as sound filtering, face recognition, or in the very original scenario, Fourier stated that any square and sharp line can be synthesized from combination of sine/cosine waves.

The discovery starts with Fourier Series, such as the white light is a composition of all kinds of color light in different waves and frequencies.

Generalized, any periodic function can be mathematically expressed as

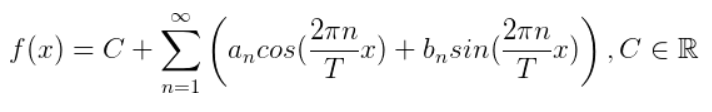
Through some vector computation, it’s deduced to

According to Euler Equation

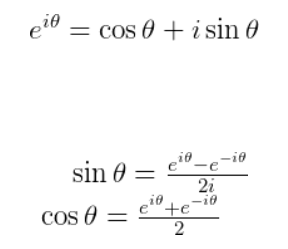
Another form of Fourier Transform is as below, exact the similar one to Laplace Transform.

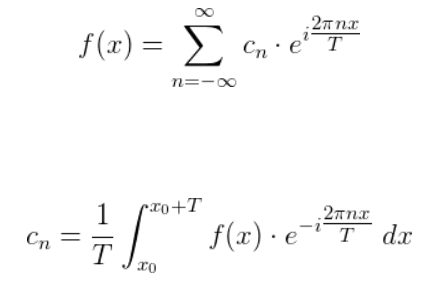
It’s worth noting that there is an inverse form too, so not only you can dissect any function to individual wave series, but also conversely, targeting one single wave from the mixture and treat it separately.

(reference from wiki, khan academy, and a Chinese blogger 马同学高等数学 )

With a more intuitive and visual way, 3B1B come up with the beats/second and cycles/second frequency combination

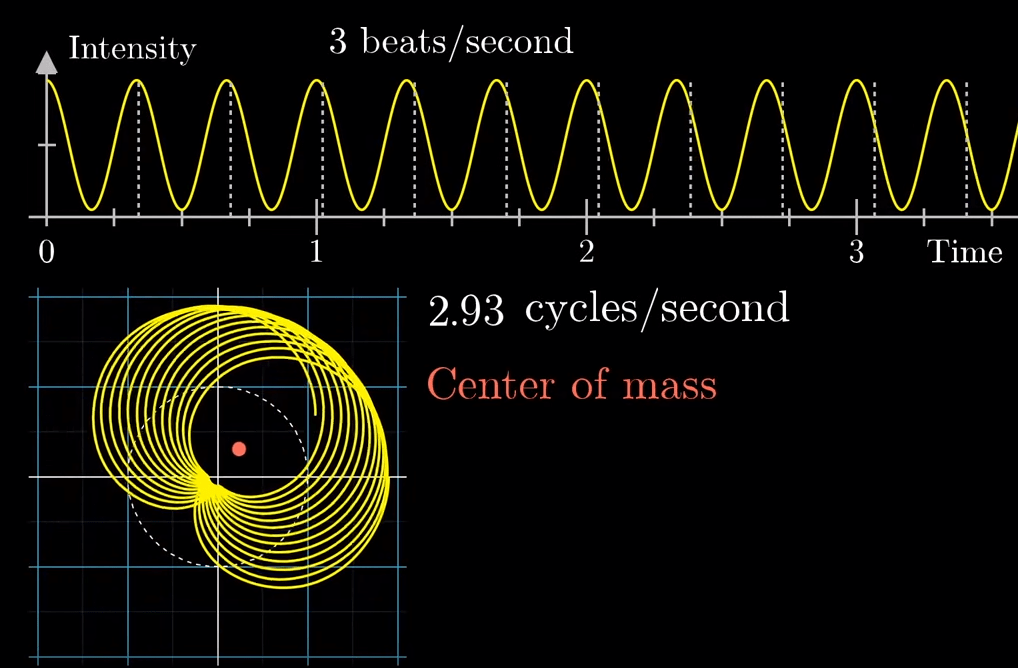
Then similarly he invoke the Euler’s formula to convert it to the form of classical Fourier expression.

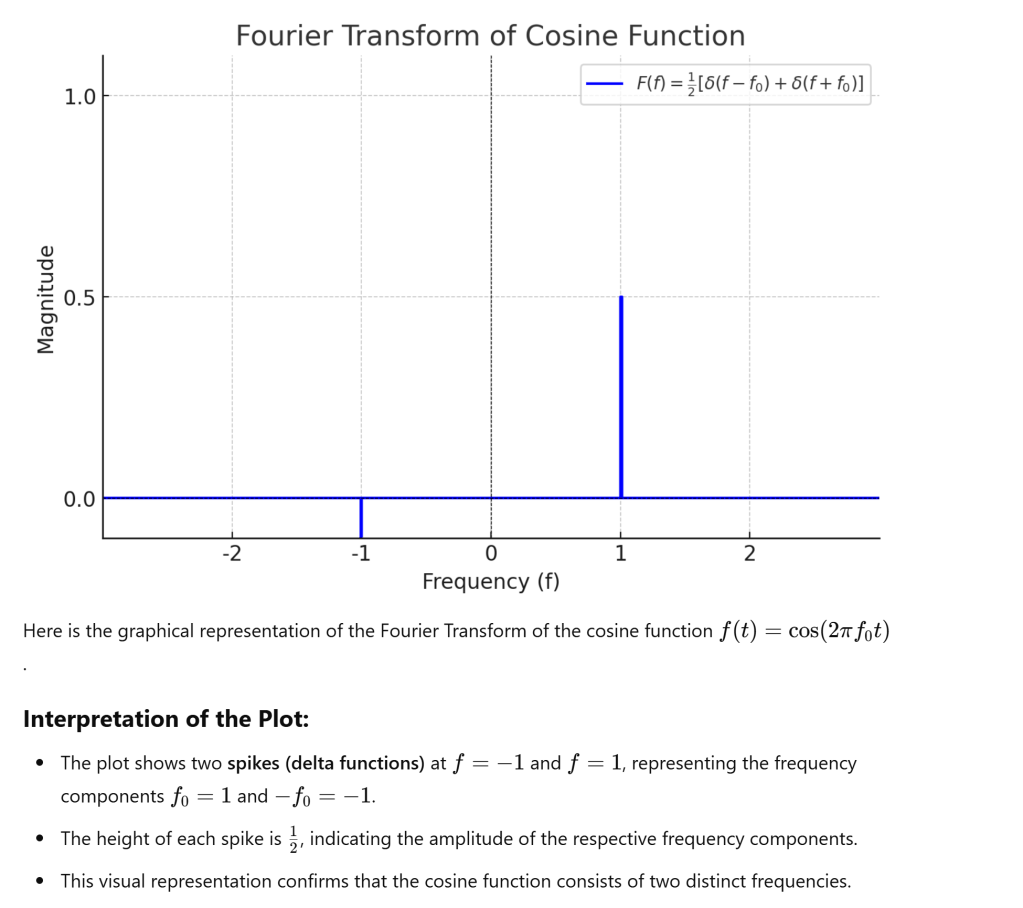
On Feb 2025, ask AI to get deeper understanding by a concrete example:

This shows that the cosine function contains two frequency components at f0f_0f0​ and −f0-f_0−f0​