To think about the title touches upon the conceptual grasp, Multivariable calculus in essence is same as the subject of Derivatives of multivariable functions.

3Blue1Brown did a great job helping me visualize the multivariable, which is related to knowledge of linear algebra too. Then comes the concept of partial derivative, gradient, divergence and curl. The following are formulas for divergence and curl respectively.

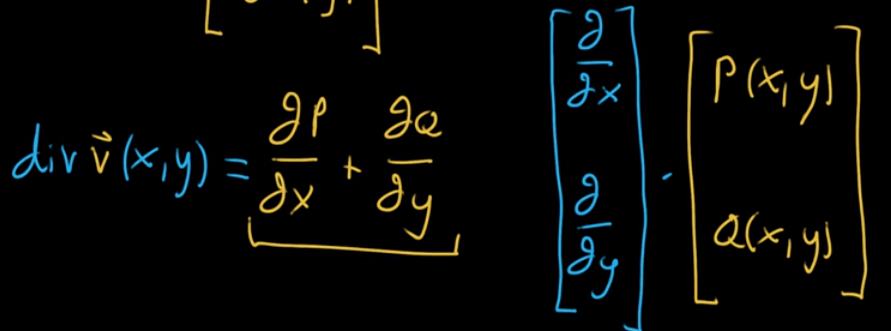
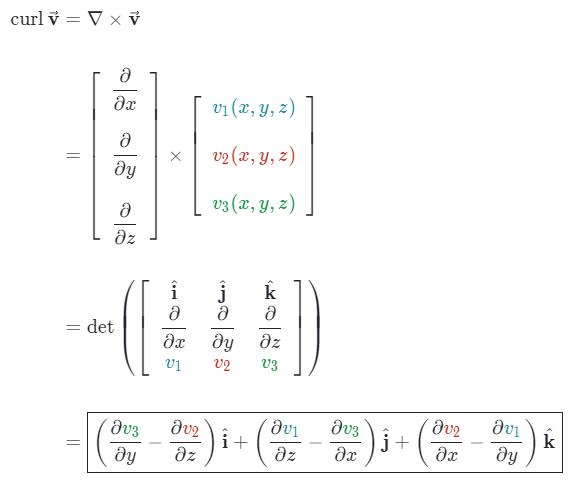
While the Laplacian operator is sort of second derivative on 2d functions, it’s the divergence of gradient of multidimensional function f.

Next, to grasp the concept of Jocobian Transform, first, several transform rules:

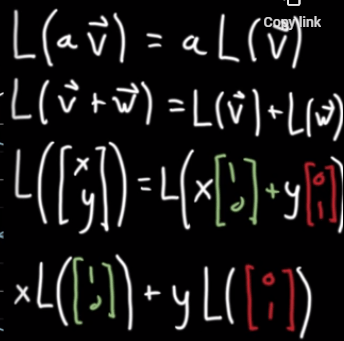
When we zoom in a tiny local area, and try to figure out how every component is transformed by leverage in the partial derivative tools, we generate Jocobian Matrix as follows:

As a result, determinant of jacob matrix can be calculated.

Revisit on Feb 2025 to reenforce this key knowledge:

Laplacian nebla squared is the divergence of gradient.

How is equation 6 deduced?

note the “dividing by the small volume” above is misleading, just think of an infinitesimal small cube and breakdown to three axis, compute the rate of change (diverging out on that direction) and sum up.