After a good grasp of theory of machine learning, we should delve into the application of it. Given my limited experience in using it, I won’t go deeper but touch on general topic – evaluate ML hypothesis.
It will take a bit significant amount of time before actual ML runnig, but definitely worthy to rigorously evaluate and choose the right model and parameters.
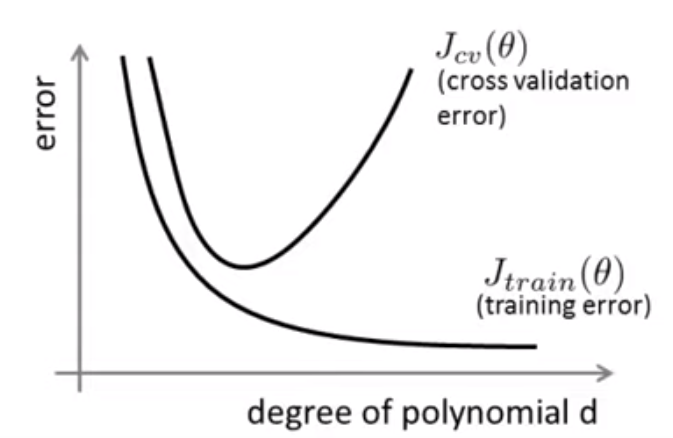
First, we encounter the question of which polynomial model to pick:

Intuitively and correctly, we should calculate the J function/cost function, which ever one that provides the minimal cost should be optimal. However, it’s well known in this arena that there are under-fitting(bias) and over-fitting(variance) problem. So apparently, the higher degree (variants) will lead up to a lower cost, which introduces over-fitting issue. The solution is to split the data set into three portions: test, cross validation and test set.
To get the concept clear and right, bias means bias of linear regression prediction; the more polynomial line, the less bias, but higher variance. Usually it over-fits, reflected saliently in classification models too.
To solve the issue of over-fitting, a math solution is regularization. Note the below cost function with the additional lamda term.

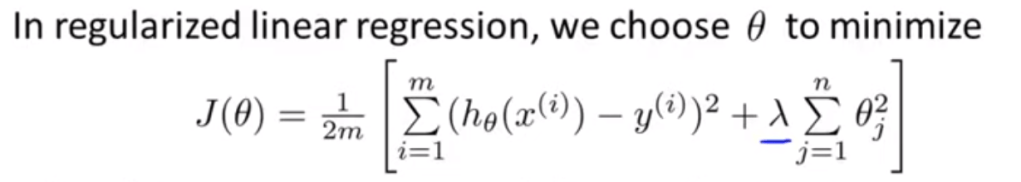
In logistic regression, it looks
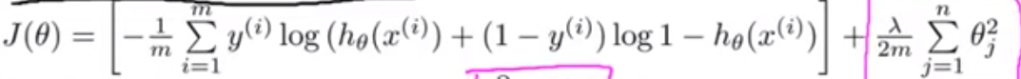
In normal equation, it looks

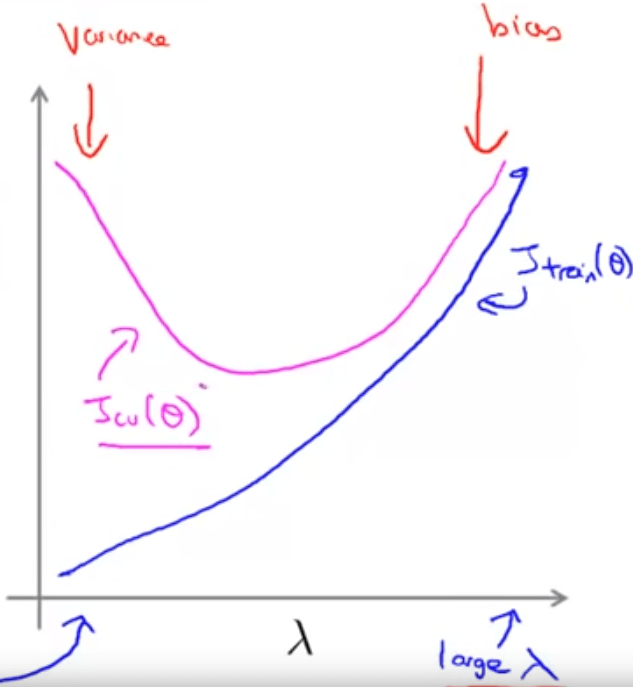
It can be visualized of how lambda controlling bias and variance:

More concretely, we can come up with stepping-up iteration of regularization lambda test, to identify the value of lambda associated to a minimal cost. Empirically, pick value doubled up such as 0, 0.01, 0.02, 0.04, 0.08 …, from the following chart, we can see clearly that either a too small or too large lambda performs horrible in cross-check data.
As prof. Ng mentioned, in real ML practice, you will need to decide if more training sample data is needed or modifying optimizing models is more necessary. Observing the learning curve of high biased and high variant cases:

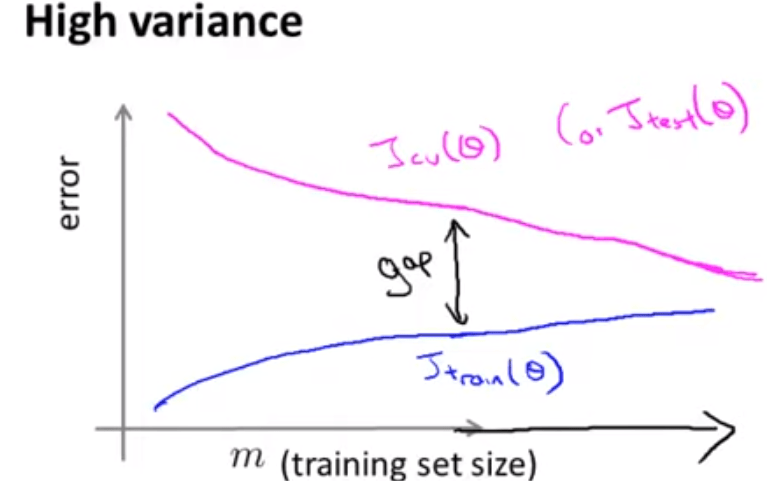
In sum, when there are unacceptable large error in your trying, the following options are open to explore and test:
