Another type of ML worth learning is SVM – support vector machine.

The math behind is similar or derived from logistic regression with some mathematical substitution to get below:

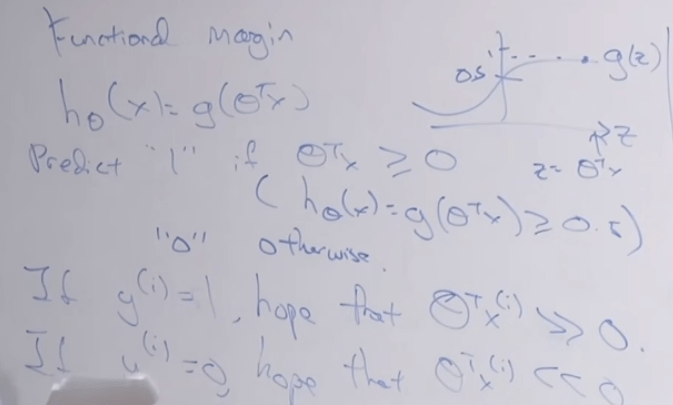
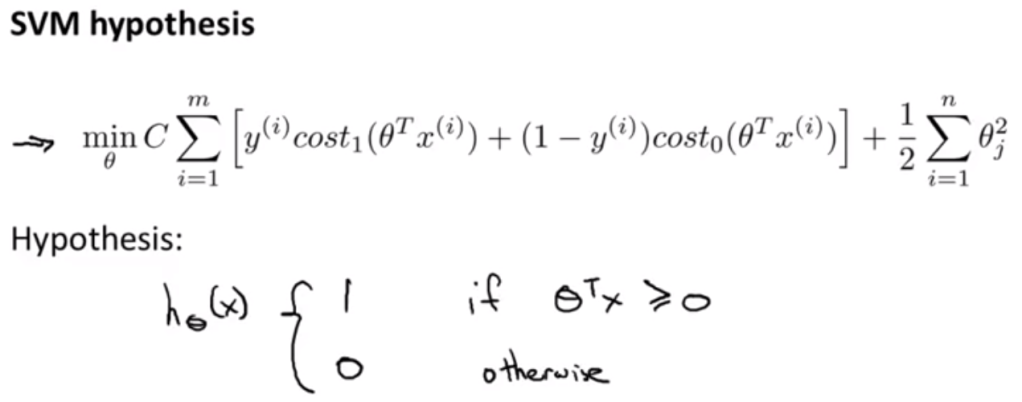
Just to make the math a little bit easier, adjust the math notation as the following:

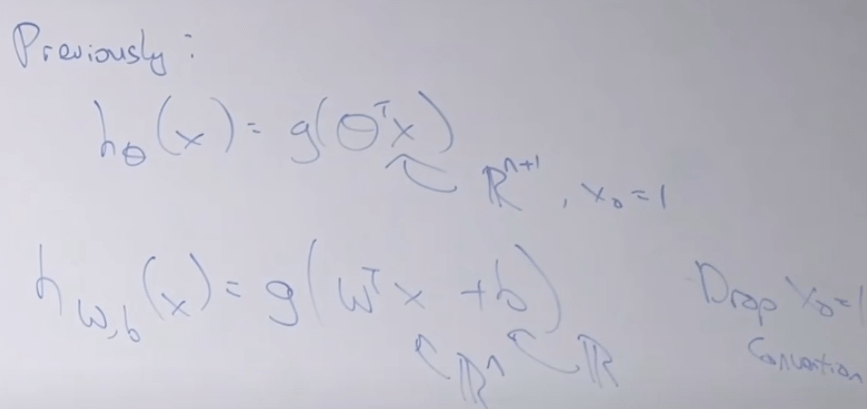
To be more concrete, it’s main purpose is to achieve higher margin in terms of vector distance between data points and decision boundary

So there is the concept of functional margin and geometric margin, in essence is inherently connected.

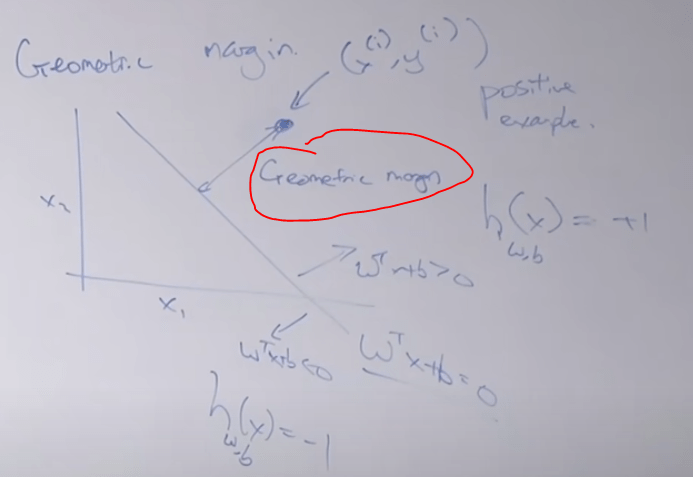
expressed as

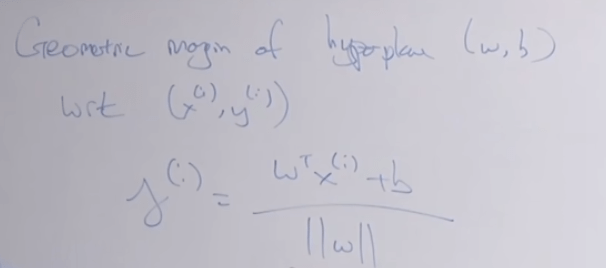
What the optimal margin classifier does is to choose w and b to maximize the geometric margin r, shown in the graph, it’s clearly the boundary line is most distant to groups of two sets of data, converting it to solve optimization problems.

To further understand using spacial intuition, here is the view, it’s formally provable as representation theorem, in which one can see that w vector is perpendicular to the SVM boundary plane.

By the way, w is mathmatically expressed as

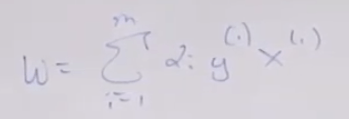
So then the linear algebra computation can be substituted into to derive the following where “inner product” appeared, which is essential in calculating vectors with immense number of features.

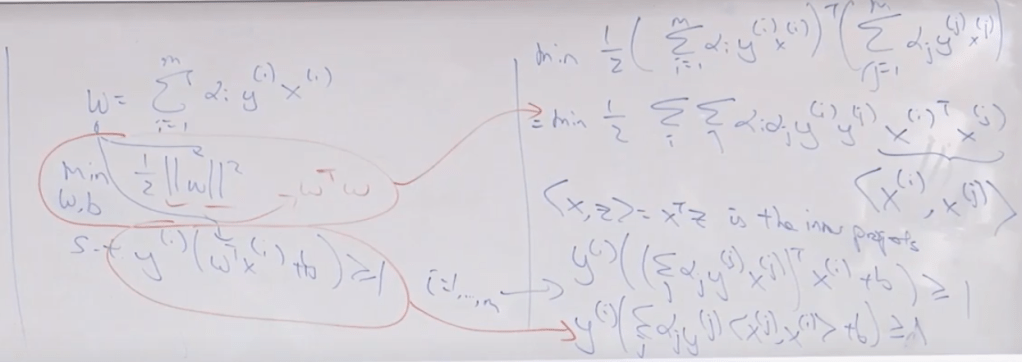
Then the problem is transformed to solving alpha and then inner product

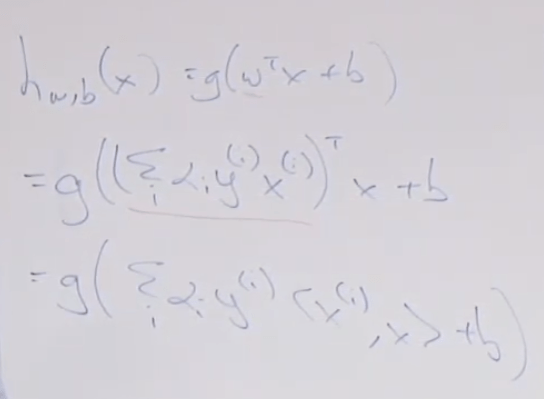
Application of inner product is reflected on kernel trick,

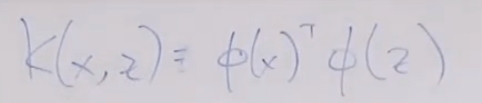
So what is SVM? SVM = optimal margin classifier + kernel trick

How to make kernels? if x and z are similar, K(x, z) is large; conversely, K(x, z) is small. is it a valid kernel, Linear kernel and Gaussian kernel is the most widely used kernels.

Introducing L1 norm soft margin SVM to address cases when there are outlier kind of mixture in groups but you don’t want to finetune to fit every single data point such as that extreme mixtured one.

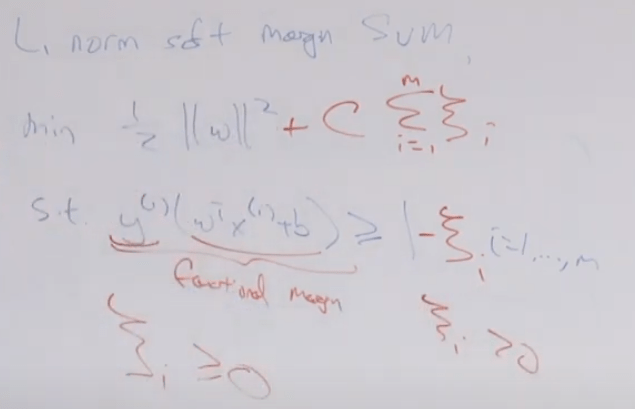
Early days, when people use SVM, either polynomial SVM(top) or Gaussian(bottom) accomplish well in recognizing handwritten digits. Later years, neural network took over and does a better job.

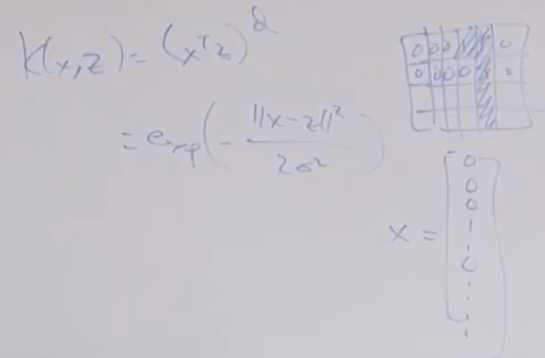
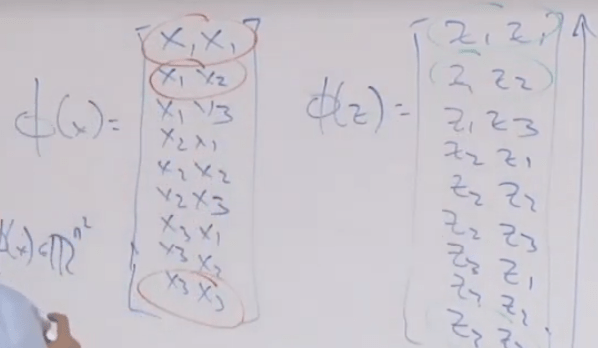
Another example would be in biology to sequence code for proteins. The design of thai(x), inner product is key, one is like

Next, Kernel is introduced to create new features and approximate. The key here is to find landmark l1, l2, l3 and calculate similarity between x and l to come up with new f. In this snapshot, Gaussian kernels is used. If x and l is very close, f will be nearly close to 1, other wise, f will be close to 0.

Then replace this original feature value x with new f here, plug into the hypothesis equation theta0 + theta1x1 + theta2x2 + theta3x3 become theta0 + theta1f1 + theta2f2 + theta3f3.

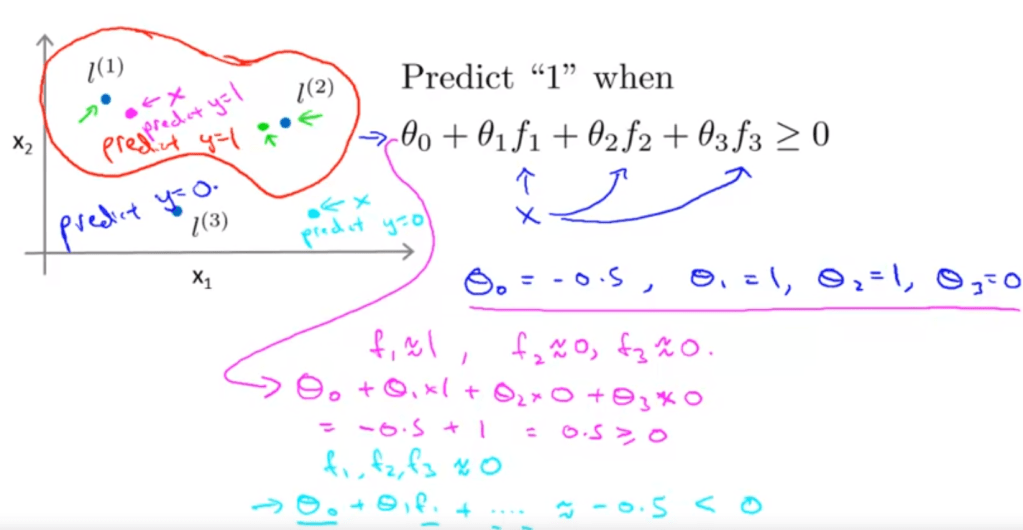
Then the question is how to choose the landmark ls? It turns out using the test data is the best way to start from. So if there are 10,000 sample/test data points, 10,000 f is created (certainly the datapoint itself gets 100% similarity or f=1), thus the hypothesis formula contains 10,000 dimensions. Kernel goes well in SVM with regard to this intensive computation – Theta(t)Matrix(Theta) , but not other algos such as pure linear regression or logistic regression.