We know the basic concept of matrix as a transform function, which could have constant “axis” no matter how it transforms like a spinning cube always lands on its diagonal line.

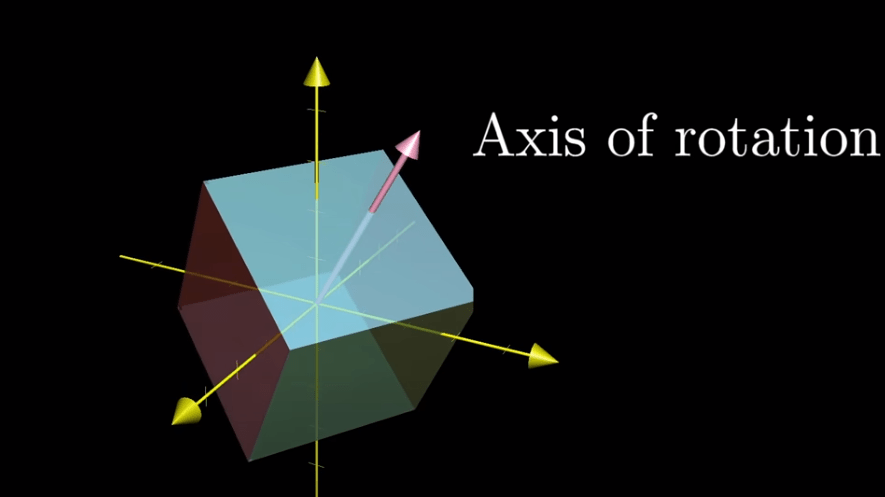
Drilling down to math language, we need to find out the vector(v), after being transformed it is the same vector except scaled up or down.

A*v = lambda*I*v

Then we solve the equation, the lambda is eigen value, and the v is the eigenvector.

Take the following 2D example from wiki: We need to find if there is eigenvector/eigenvalue for this matrix A, if yes, compute them.

The notion of eigenvalue seems to more intuitive, but what about the eigenvector v here? it should be any vectors according to the equation, from above deducing, there is only two vectors [1, -1] and [1,1] satisfies, corresponding to lambda 1 and 3 respectively. (there is an animation on wiki page illustrating it)

Additional insight from Dr.Strang at MIT 18.06,

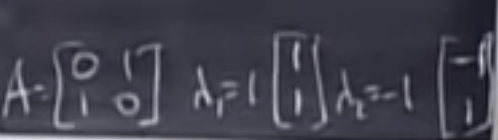
If we add 3 on diagonal position, its eigen values need to add 3 while eigen vectors kept same.

The more symmetric the matrix is, the more likely it will get a real number as eigen values, the more asymmetric, like rotation, the less, and the extreme is to have complex number as eigen values.

Another case, if the opposite diagonal has zero, the eigen values repeat, how to find the eigen vectors?

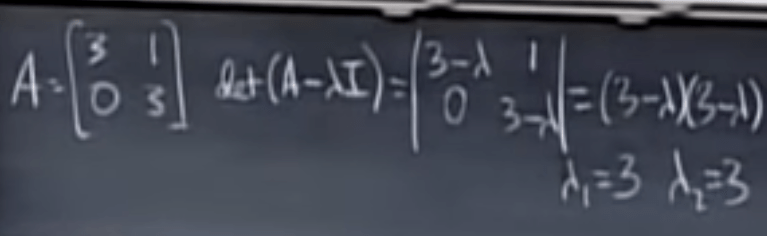
It’s a degenerate matrix,

Practice

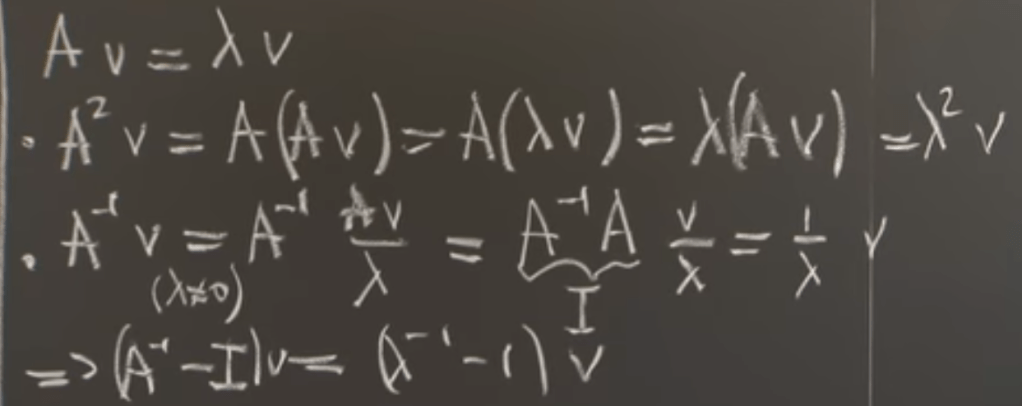
We can dragonize and power matrix composed of independent columns(invertible)

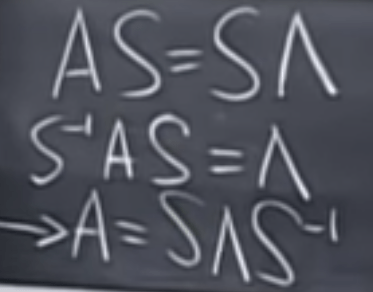
observation based on above, one can easily infer that if |lambda| is less than 1, it will go to zero when approximate to limitless.