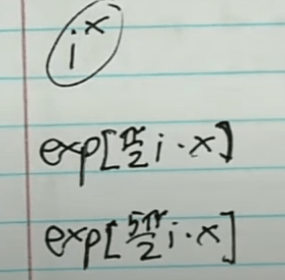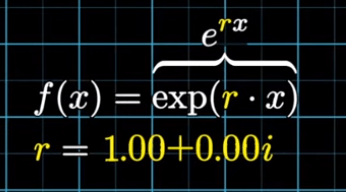It starts with a mind-boggling question. What if the bank offers you an interest rate of square root of negative 1, will you take it?

Starting from the simple math, hypothetically save amount M dollar into a bank, one can reach

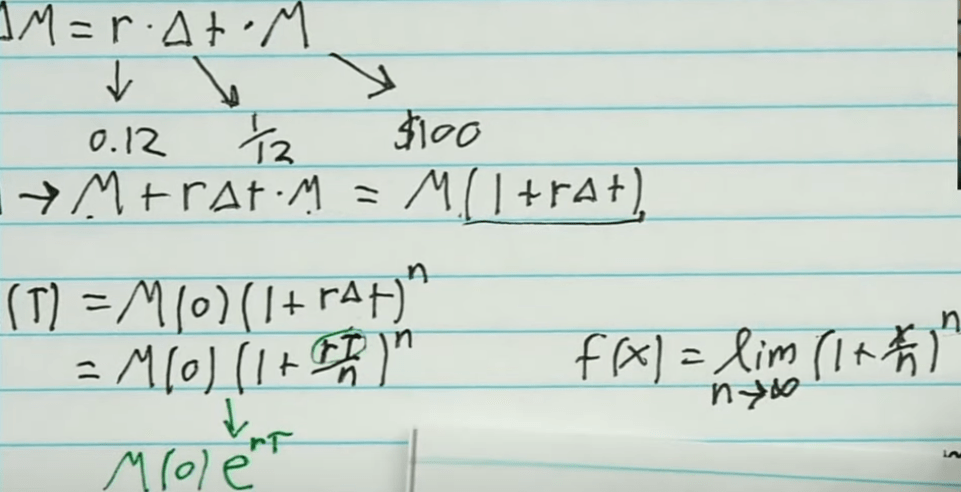
e = (1+1/n)^n, e’s exponential r = e^r = (1+r/n)^n. r could be imaginary number as in the following narrative.

Before plugging in imaginary interest rate, I’d ponder how to picture e raised by a complex number, why it turns out to be a circle and is so widely used in quantum mechanics? In essence, transform these seemingly non-sensical numbers into geometry language. adding in i into the expression makes it drawable in complex coordinates:

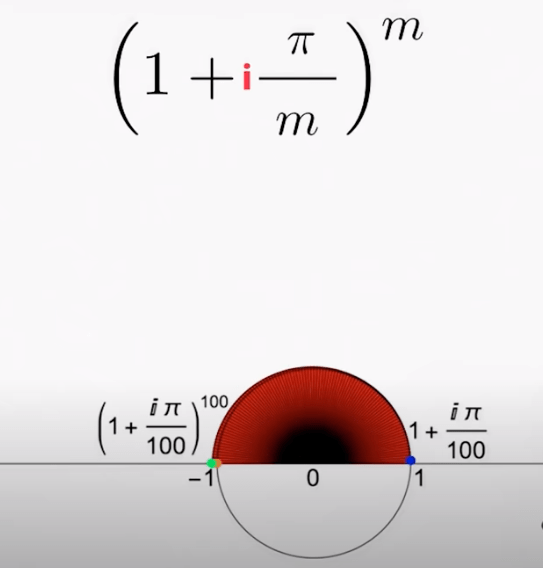
Hence we should always have the math intuition that

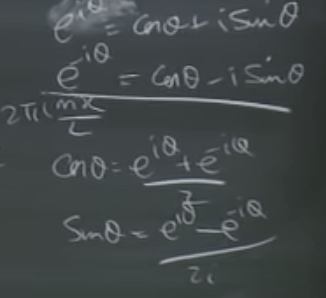
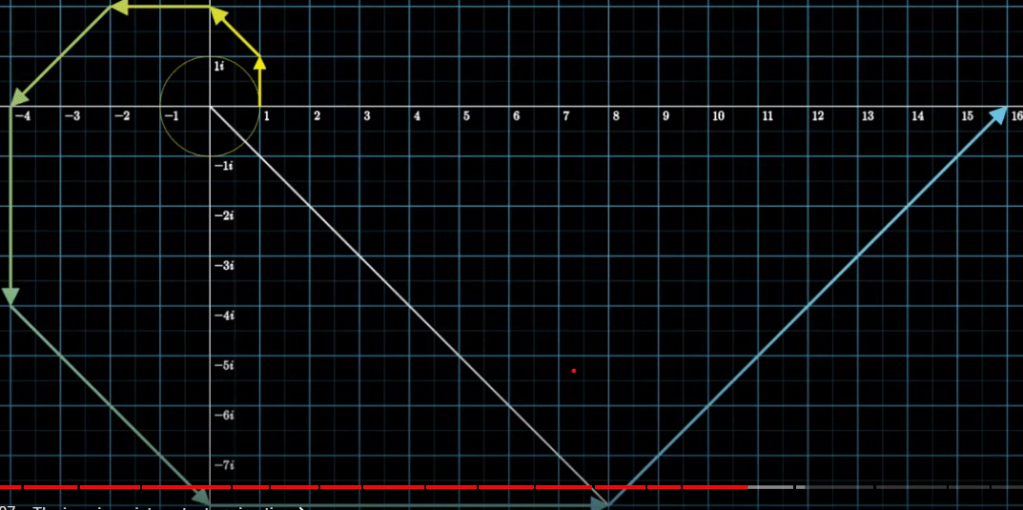
And if you apply continuously infinite periodical compound interest rate, the spiral shrinks to as below and ultimately just nearly be a full circle, meaning what ever money you put into the bank with this interest rate of square root of negative 1, the return is zero.

It is elucidating and also fun to see how negative imaginary number interest rate plays out, but more essential is to note this continuously compounded interest rate yields a magic number e, natural constant. (this video clearly explains how e comes into such a critical role in equating complex number, vector multiplication, cos sin and everything in math…)

Further, in a series of number, we can see

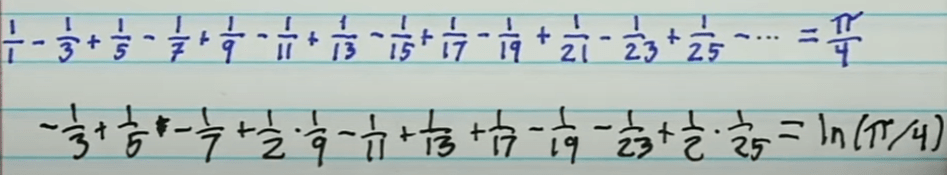
Leading to the core intriguing point here – still about e. What’s the key property of e? It’s derivative is itself:

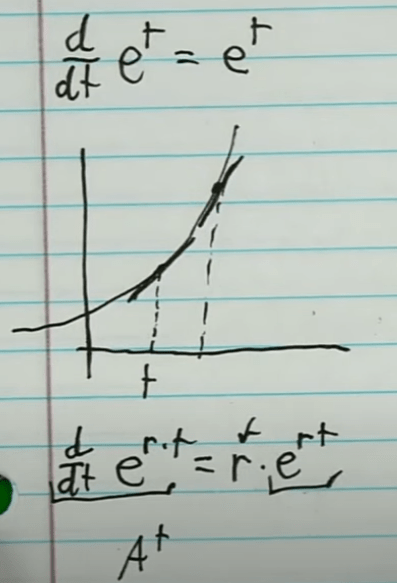
To make sense of e being raised by a value, I learned from physics and also above video to be naturally thought of as a complex number in circle, while 3b1b Grant likes to literally conceive it as an infinite polynomial as below, of which, the two actually and certainly equates.

Hence, if one deeply understands Euler’s formula in describing above, to solve the following problem is intuitive:

Because what it describes is an object obeying Euler’s formula – moving around the circle periodically. So after t time it goes to the corresponding e(it) position.

So it’s more and more clear, all Grant wants to clarify is that this e, or exponential expression exp(rx) (exp(1) = natural constant e) is actual infinite polynomial and the key to grasp is their central property of f(a+b) = f(a) *f(b), such as

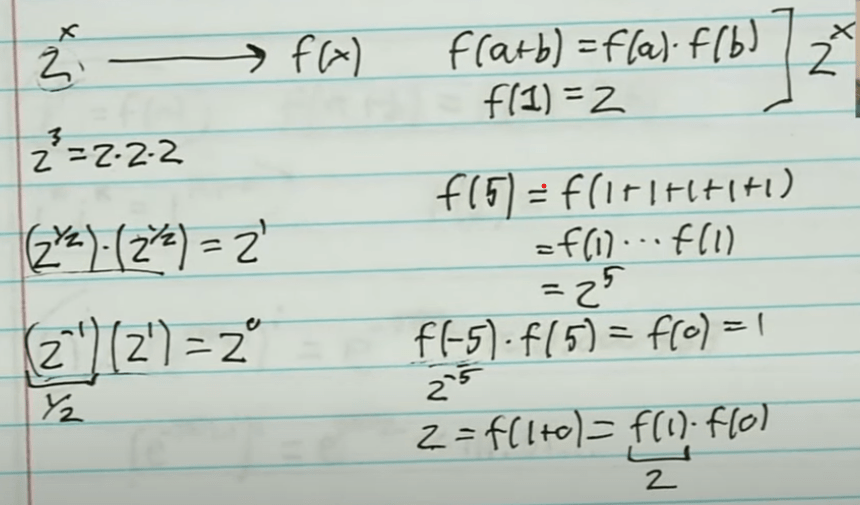
That ultimately explains why i raised to x could have multiple solutions