Claude Shannon, father of information technology today is worth my research. I started from the very basics of crypto theory. He describe the concept of “perfect secrecy” by such a story that you went into a room only given several locks, a deck of cards and an empty box, you pick a card and then leave the room without carrying any items with you, the purpose is to keep anyone entering the room again from knowing which card you picked. The initial thought of placing that card into the empty box and then lock it is fragile after a little deeper thinking – anyone can figure out which card you picked after checking the remaining 25 cards to see which one is missing. So the perfect way is not to single out that card, but shuffle it into the mixture. This is what Shannon called “perfect secrecy”.

This reminds of the clever way people crack Caesar codes other than brute force. The secret is hidden in the letter frequency distribution, which is like a fingerprint of each letter. Similarly, an expert can tell a sequence of 0 and 1 is formed by flipping coin randomly or a person trying to mimic that randomness (pseudo-randomness) by detecting the sequence frequency distribution, such sequences as 0000000, 1111111 etc. True randomness is equivalent to non-deterministic, unpredictable.

How to create randomness? In inventing hydrogen bomb, Neuman actually had to resolve this problem and he came up with this strategy, first come up with a seed number, then square it, choose the middle three, then square again, choose the middle digits again, this approach is called middle-square method. The random sequence is entirely dependent on the original seed number. Now the question to ask is that is it a true random sequence? if the original seed value is single digit, say 2, then 2, 4, 5, in no time, 2 gets to be recycled/reused again and then the sequence repeats itself, obviously, it’s not a true randomness. This seed approach however, still has a wide use because if the seed number is large enough, it takes long long time to reach to that period. So pseudo-randomness is practically safe.

Public key cryptography – Diffie-Hellman Key Exchange, this lead to the invention of RSA encryption in modern era. The key crux here is to come up with the private key. Given that it’s so hard even for machines to decompose a large number to its prime factorization,

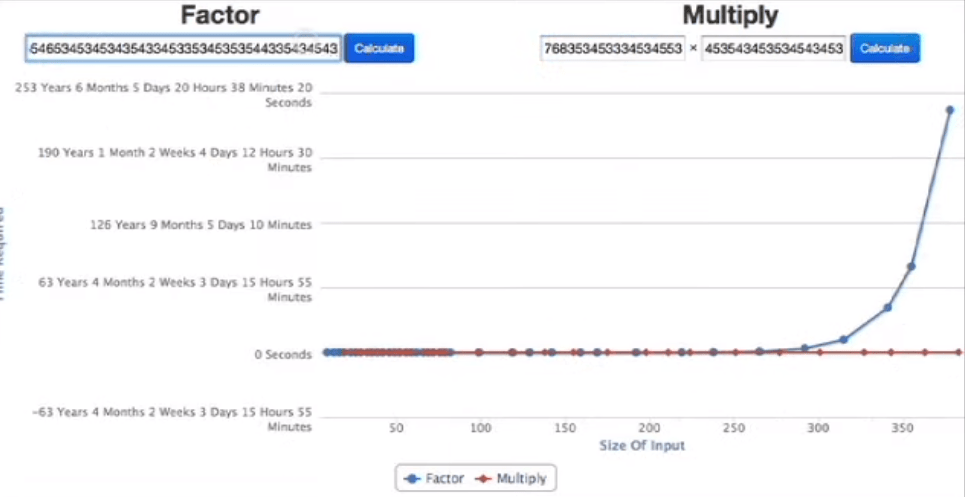
So there is this concept of phi function, the number of unbreakable values within a number.