It’s 3b1b first instill the question and answer of what exponential really is. We should not just simply apply it by multiple the subject exponential value times. What if the value is a nonsensical value? What if the value is a complex number?

Most of us feel comfortable to do add, subtract, multiply and divide. Mathologer is able to show a magical way to transform exponential computation to simple addition, subtraction, multiplication and division. He starts with deducing natural number e = (1+1/N)^N, then e^pi = (1+1/N)^Npi = (1 + pi/Npi)^Npi = (1 + pi/m)^m,

According to 3b1b Grant, e^pi can be expressed as follows:

certainly, e itself is

However, using this infinite polynomial, you still can’t figure out what’s (1 + pi/m)^m, if we use the aid of geometry, it can be draw both sides and when m goes bigger and bigger, the two curves match to perfect.

Next, what if there is an imaginary part in the exponential position.

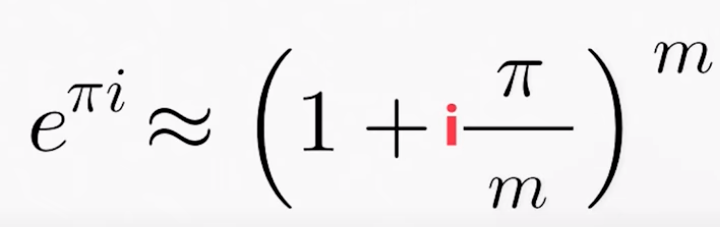
To make sense of complex number multiplication, Mathologer turns to geometry animation again:

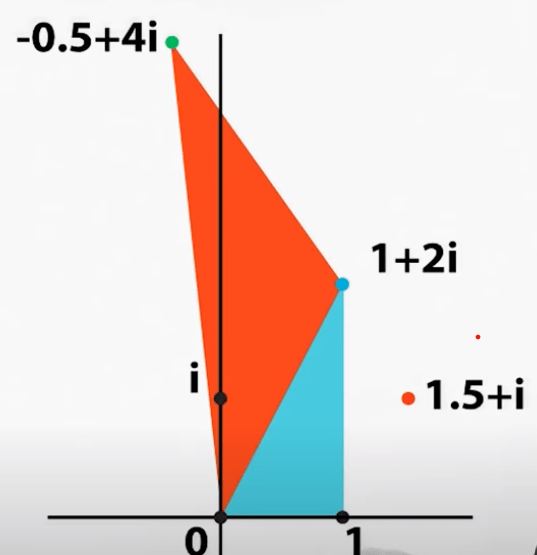
As to why so, 3b1b’s guidance on applying pivoting axises provides some rope but not exact clue.

In his explanation, a matrix times a vector is a linear transformation as follows. However in this context, complex number has the i part(actual number 1) and j part(imaginary number i pi). (need to search for complex number multiplication because the 3b1b linear transformation does not fit here)

Back to this problem of inserting i next to pie, if m is small, say 3,

When m goes bigger and bigger, at the number of 100, it already looks pretty close to -1.

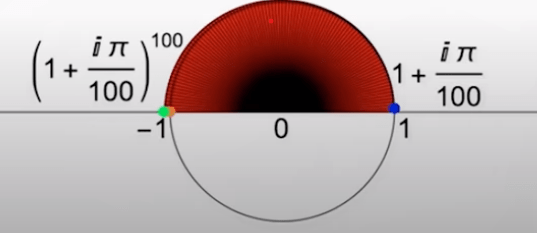
Beautiful, I am particularly amazed by his ability to reduce the abstract raising complex number at exponential problem to some straightforward basic math problem. Further more, 3b1b demonstrate another novice perspective using lens of calculus.

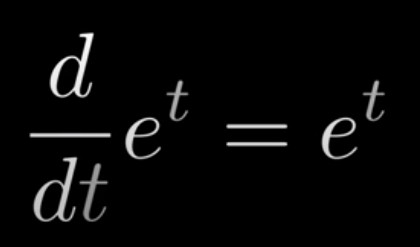
He does not look at the e^t statically, but applying d on both top and bottom – converting to look at the velocity and draw out the trajectory. Then tweak the t with 2t, -0.5t, to i*t.

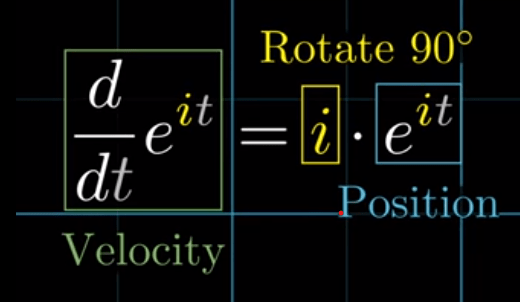
to deduce

Finally I learned how this infinite polynomial equation is the accurate expression for e^pi talked by 3b1b, thanks to prof. Steve Brunton in his math review

Note one should be familiar with solving the linear DE to get

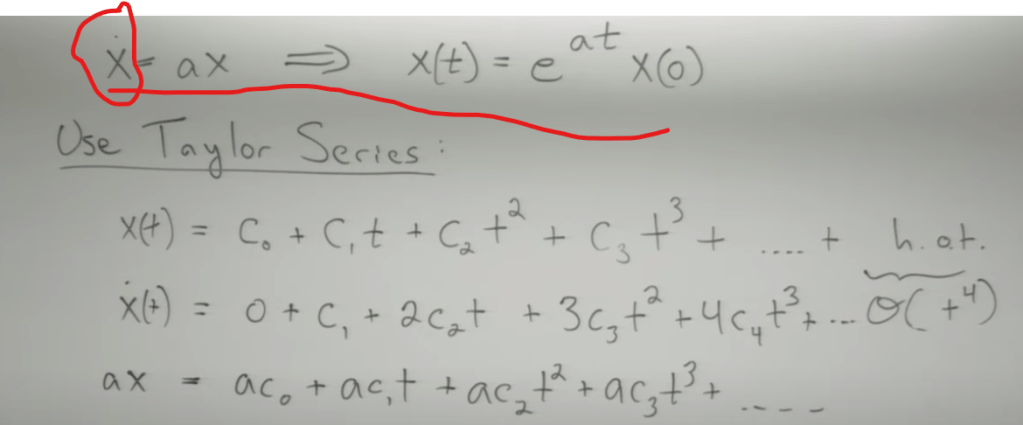
Use Taylor Series as any function/curve can be expressed by zero order, one order, … multiple order of t, now you just need to plug in x’ = ax (this satisfy linear/simple ODE) over and over again when the order of derivatives goes up and up.

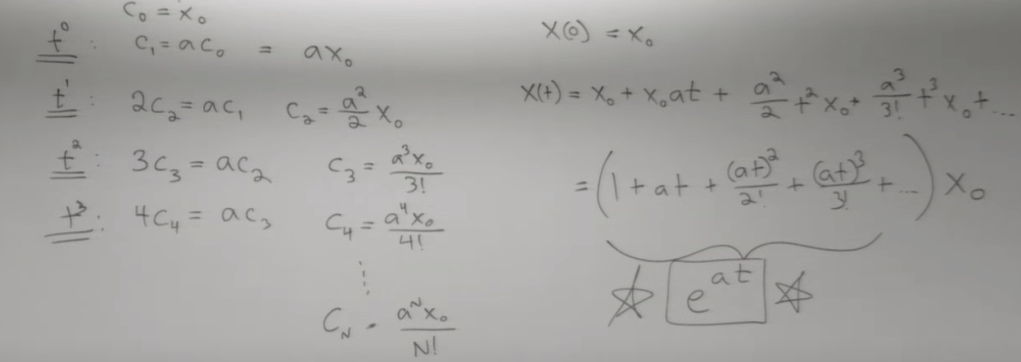
Then in the future, we can replace the real number a with a matrix A to compute

add on Feb 2025:

4. Why Is eAe^AeA Useful?

• Solves Linear Systems: Appears in differential equations as eAte^{At}eAt.
• Describes Rotations and Transformations: Used in Lie group theory (e.g., robotics, control).
• Simplifies Computations in Quantum Mechanics: Used in quantum evolution equations.