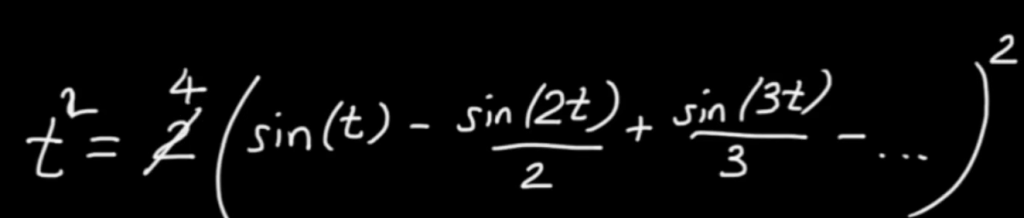Fourier became so famous now but the origin of this theory is to solve the heat equation. What on earth relates this heat diffusion problem to sound signal synthetization in modern days? I think the key is Fourier’s ingenious approach to use sin/cos wave to approximate any lines and then be able to solve the DE equations.

It can be understood as a summation of circular path/functions to form another holistic view of these circular paths like

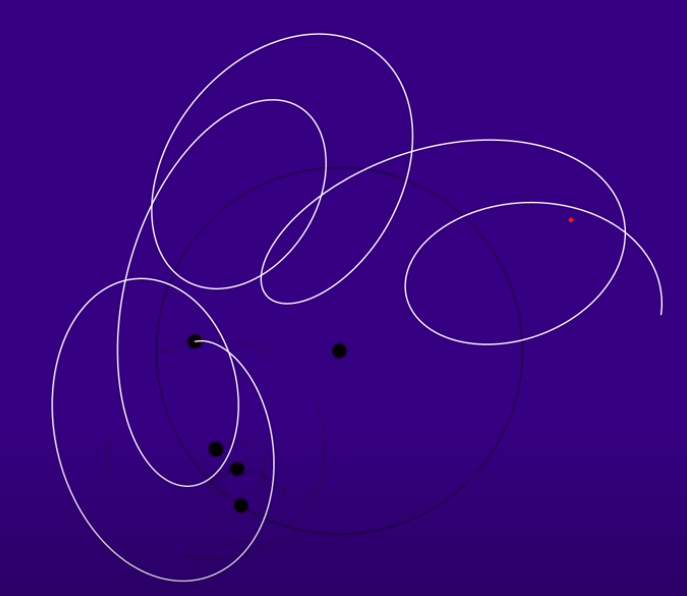
Which is derived from this equation: V1 + 2iV-3 + pi/20V-7 + 0.6V8… If it’s hard to imagine how a bunch of functions govern the movement of one single dot simultaneously, think of the planets – sun, earth and moon circling around simultaneously. In this video, the abstract relation is touched upon however still quite hard to conceive, so I just pasted the critical picture for future thinking.

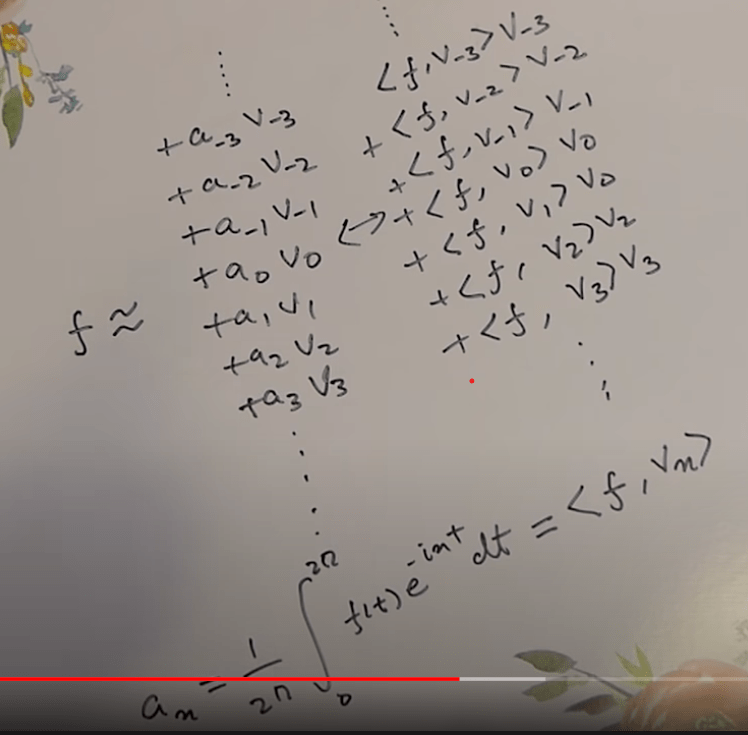
It’s now easy to see that if in 2D space, we can express any vector w as the addition of its projection on both axis vector <w, v1>v1 + <w, v2>v2, it can be generalized on unlimited dimensional space to express any functions, which is Fourier series.

However the most classical way is provided by Sal at Khan Academy, on the principle premise first proposed by Joseph Fourier that any function/curve can be expressed by combination of series of sine and cosine waves

Using the simple square wave form, he inferred the equation as follows and visualized it

Fourier analysis has many scientific applications – in physics, partial differential equations, number theory, combinatorics, signal processing, digital image processing, probability theory, statistics, forensics, option pricing, cryptography, numerical analysis, acoustics, oceanography, sonar, optics, diffraction, … (from wiki)

On the other hand, we need to understand the core of Fourier that it converts time domain signal to frequency domain signals.

To go deeper, I want to know how to apply Fourier Transform for financial derivative pricing.

On Sep 2021, from learning the Basel problem we can get a new perspective on interpreting Fourier Series as

y = t is a square line, but we can square t or take cubic of t like