Steven Brunton from University of Washington reviewed basic math before going deeper:

chain rule is

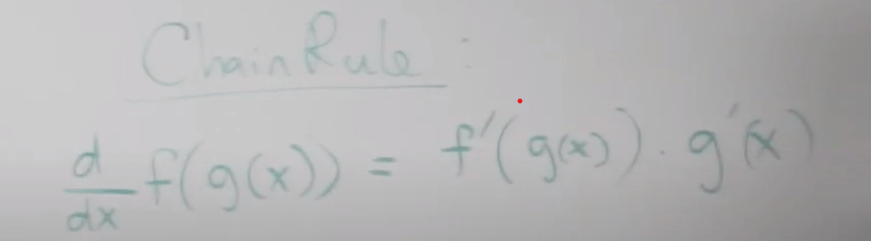
then jump to Differential Equation, starts with a bunny example

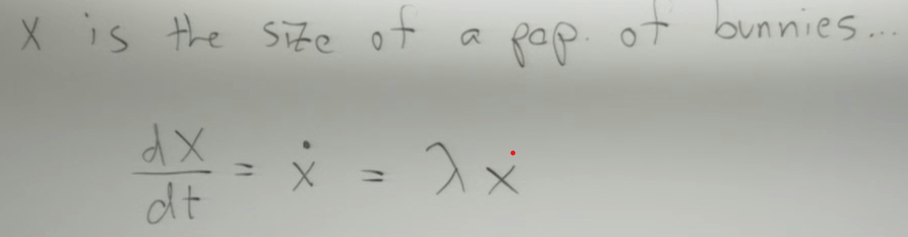
now the question is to solve X relative to the variable time (t), we do it by integral

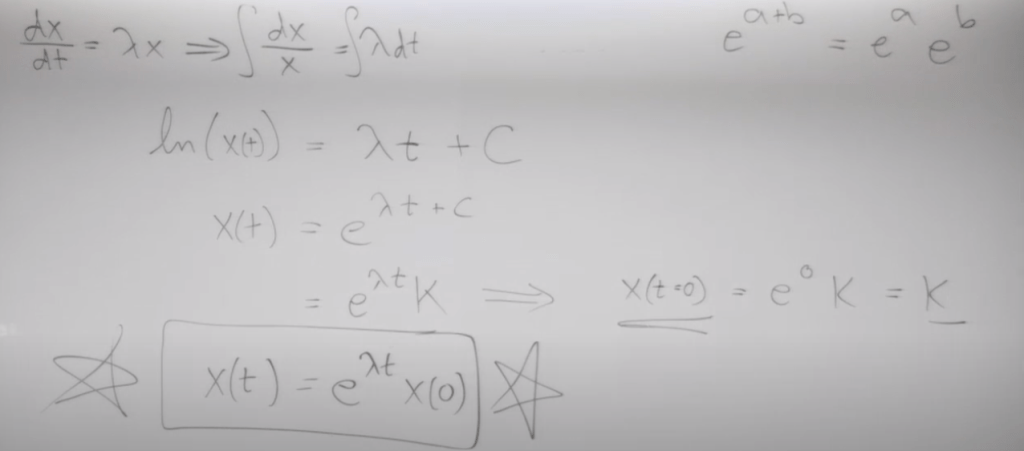
Taylor Series is universal and powerful. From above ODE computation, note Taylor series cannot be used if the function/curve is kinky or discontinuous:

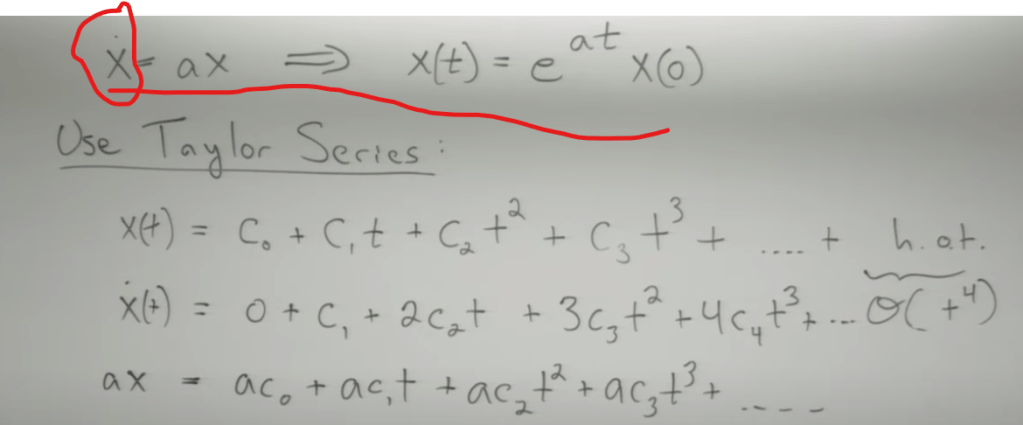
Use Taylor Series as any function/curve can be expressed by zero order, one order, … multiple order of t, now you just need to plug in x’ = ax (this satisfy linear/simple ODE) over and over again when the order of derivatives goes up and up.

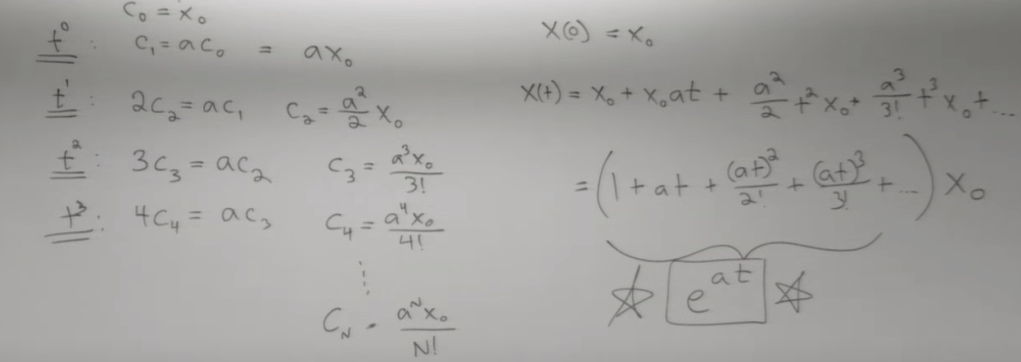
Then in the future, we can replace the real number a with a matrix A to compute, note instead of a*t, it is matrix A * t here. t is hidden in ODE.

Next, second ODE. a typical example is spring movement governed by Newton’s law

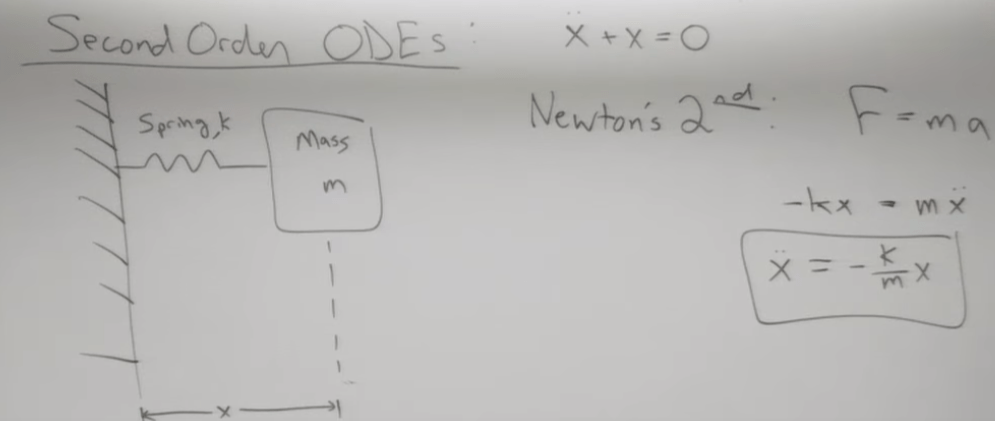
In Steve’s online course, I got in touch with the homogeneous solution for ODE the first time and was quite baffled. Now a while later when I systematically approach math using Richard Williamson’s text book, it’s stunning to see how a classical explanation of solution to Ax = b has the form of a particular solution plus homogeneous solution: