Further about eigen value and eigen vector.

Suddenly I realize eigen vector is a special vector(s) that after squished or squashed by a matrix A, it’s just scale up or down on it’s own direction. The multiples it scale up or down by is the eigen value. Not every Matrix has eigen values or eigen vectors. Since on that specific direction there are numerous vectors all qualified as eigen vectors, so a succinct expression of the series of eigenvectors is

Now use simple example to solve eigen value and eigen vector

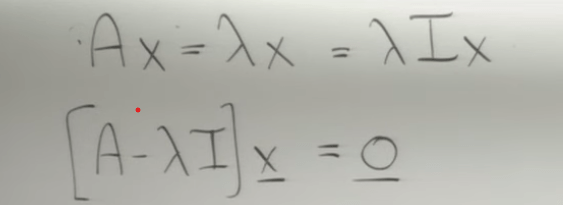
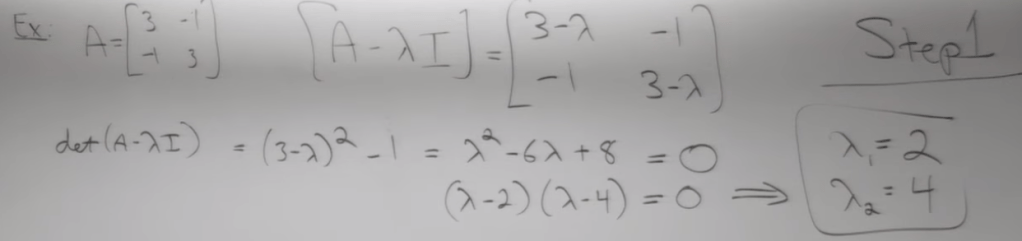
once we solve lambda, then place it back. then solve eigen vectors. Note that both lamba1 and lambda2 are written in the solutions as linear combination of the two, (get rid of elementary algebra that the solution is either lambda1 or lambda2), why? It’s due to the linear property of linear systems.

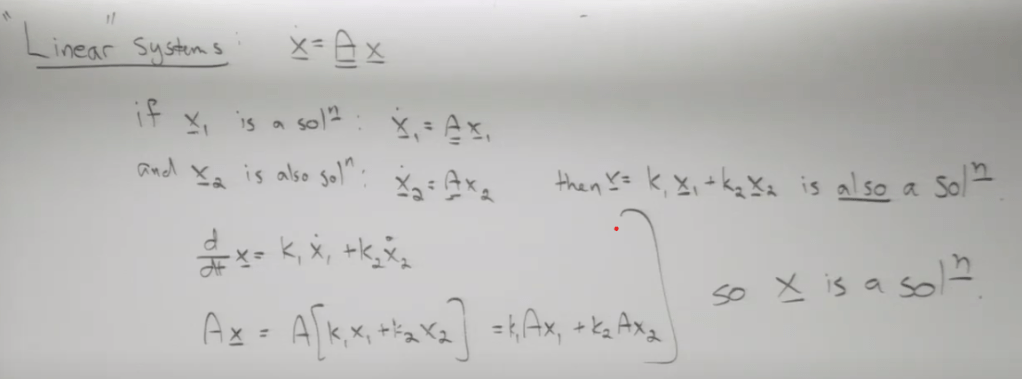
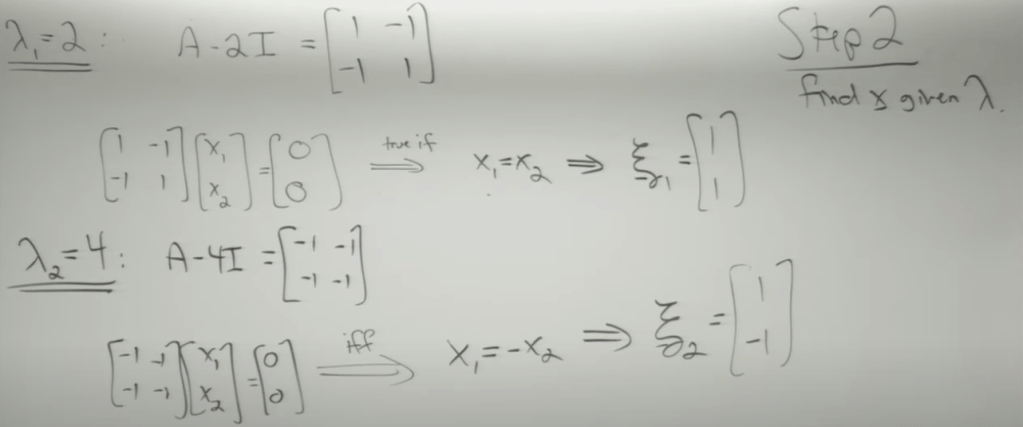
After grasping above concepts of eigen value and eigen vector, then to apply them on the Matrix linear ODE

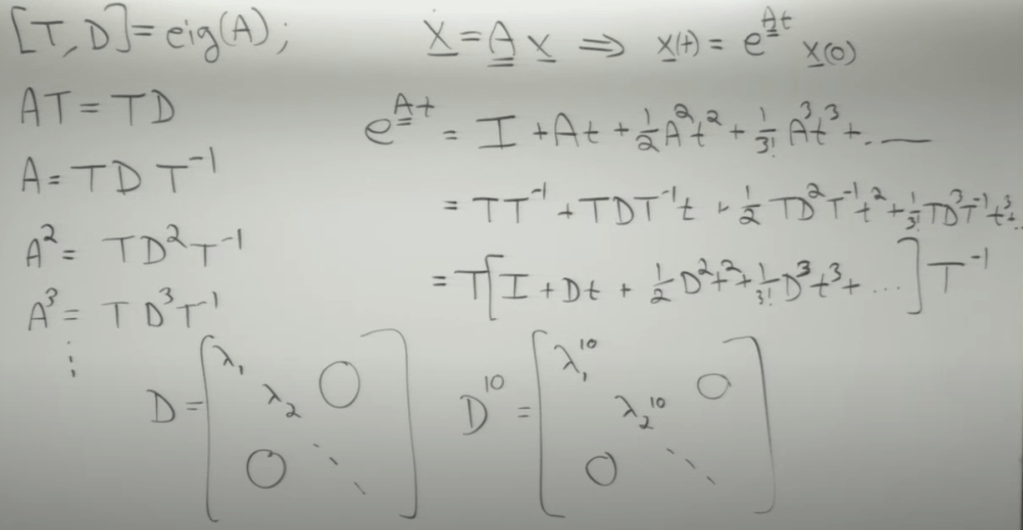
recap:

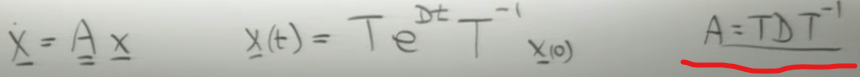
Using a simple example again, one should be able to compute T-1 either by hand or by computer, then solve the equation for X(t) and V(t):

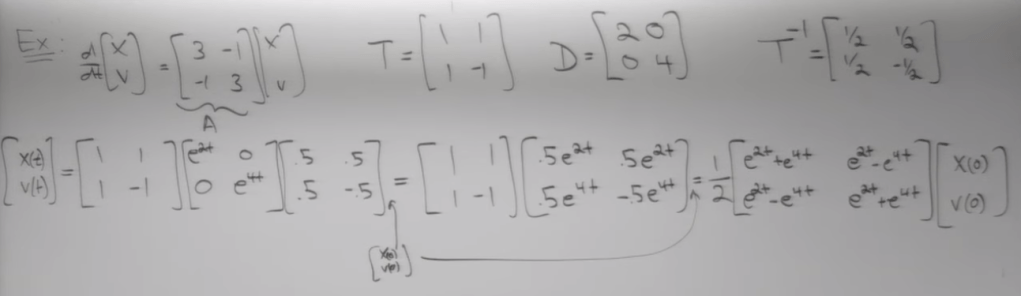
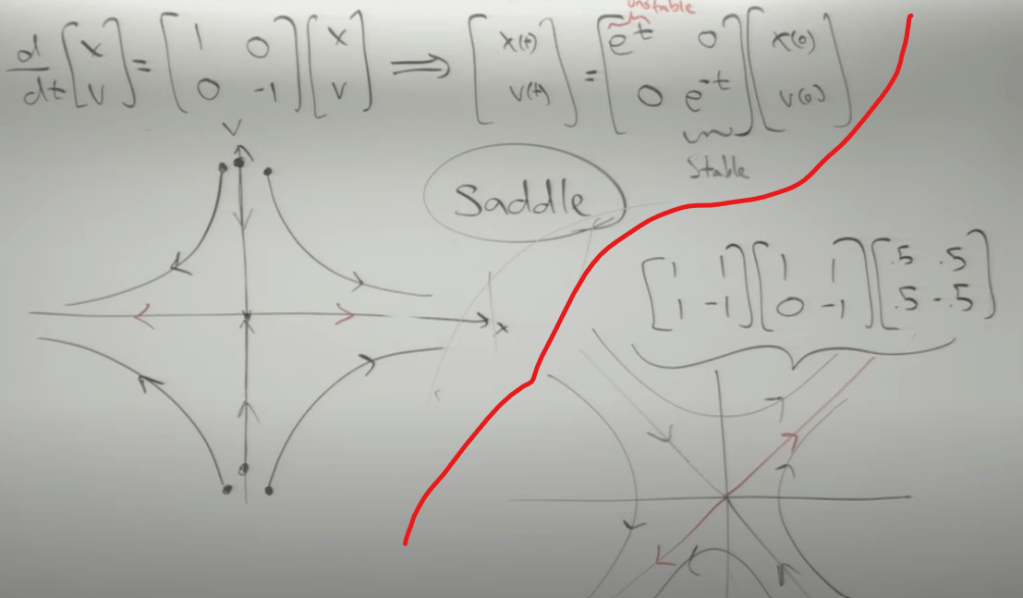
Phasing into the concept of “phase portraits” now. Two vector lines are called invariant manifolds, while any particle staying outside of these lines, will move on the sketched lines…,

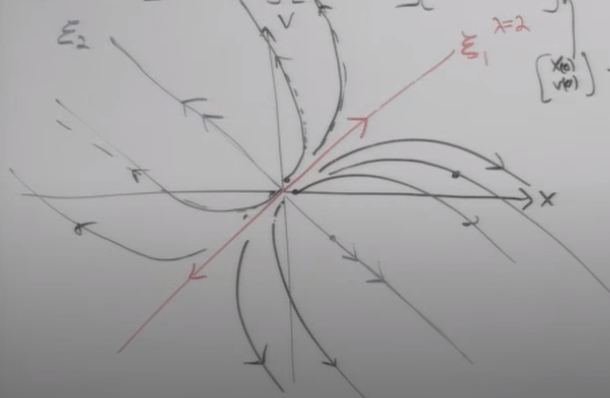
Another example is a saddle phase portrait:

Third example mimicking an undamped physical spring, expressed as the following equations

matrix A is a matrix composed of real number, so even the lambda contains imaginary number i, when we solve the whole T r^DtT-1, the imaginary parts will cancel out and yield only real number…