I heard of “indeterminant coefficient”, what is it? It’s first encountered in solving this differential equation with Force or inhomogeneous equation. By applying ke^-3t we need to “determine” the “k” = 1/2 as follows:

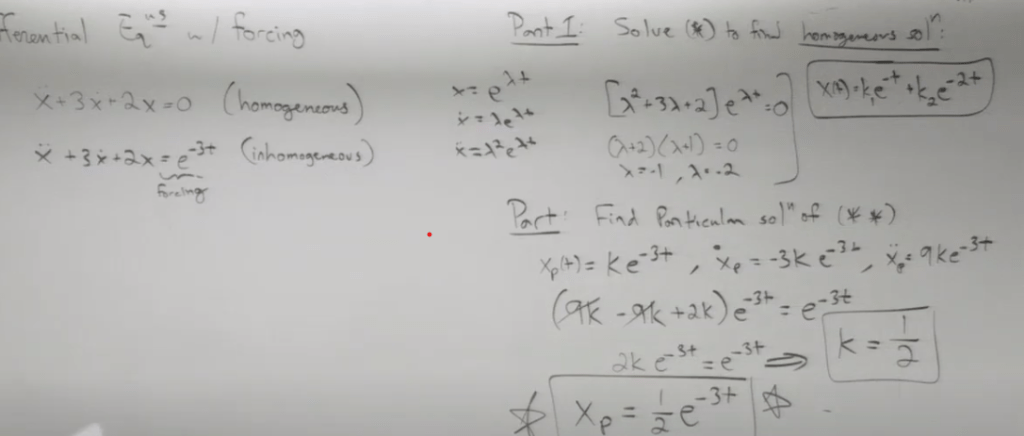
The whole solution is simply to add them up

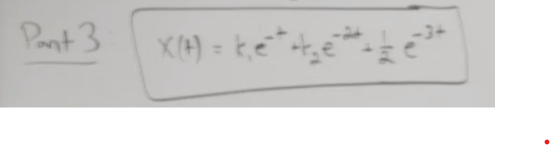
Next, let’s solve it by introducing a variant u1(t) and u2(t). We got exact the same solution. We call is “variation parameters”.

But this approach is more general than the former one where the “force” part can be guessed out as ke^-3t.

Reverting back to the first naïve approach, it always bothering to not be able to intuitively relates solution to a homogeneous(general part) adding inhomogeneous(particular part). If we don’t add the homogenous part, we might miss some possible solutions. Why? Professor Brunton explains as follows:

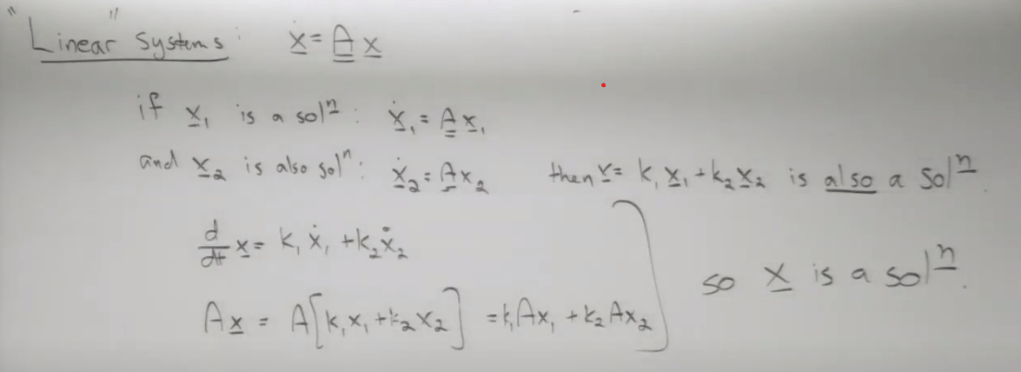
This explains perfectly in ODE world, if there are two solutions/eigen values, the complete final solution is the combination of the two eigen values (in elementary algebra, you would think it is eigen value one OR eigen value two).

However, how to make sense that zero is general or homogeneous case, also constituting a solution to this ODE? Note the external force part f(t) is not a dependable X dependent on t, but an entirely separate variable based on t. So, when parse it out in matrix form, it’s the same equation X’ = AX. X’ = AX is equivalent to X’ = AX+B.

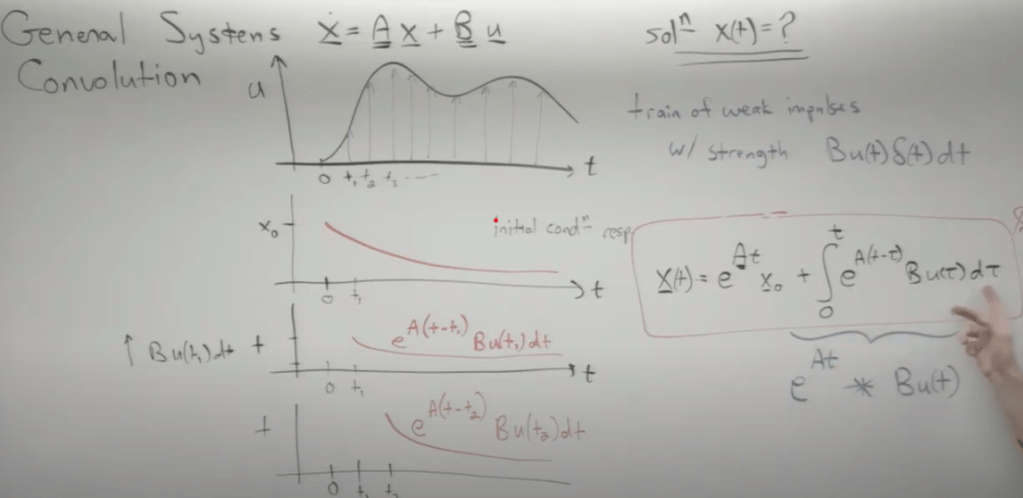
Further, what if the external force is a vector – general system of convolution.