Differentiation problem, ultimately should go back to its very origin, algebraly and geometrically as below

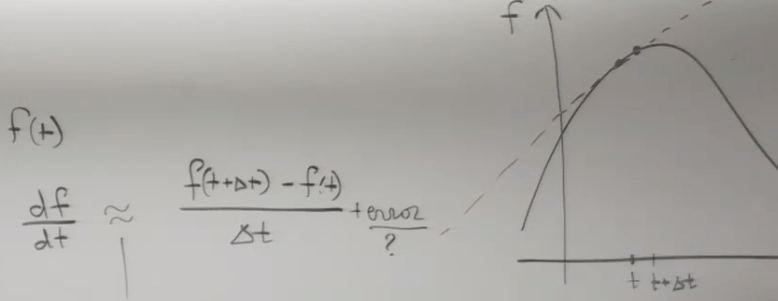
Using Taylor series to expand forward and backward approximation:

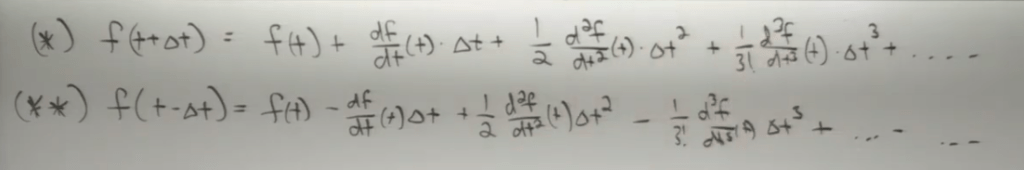
So the error part is easy to deduce. neither backward nor forward approximation approach is ideal for calculating the derivative f’ at time t using the error part as metric. The best way is central differentiation:

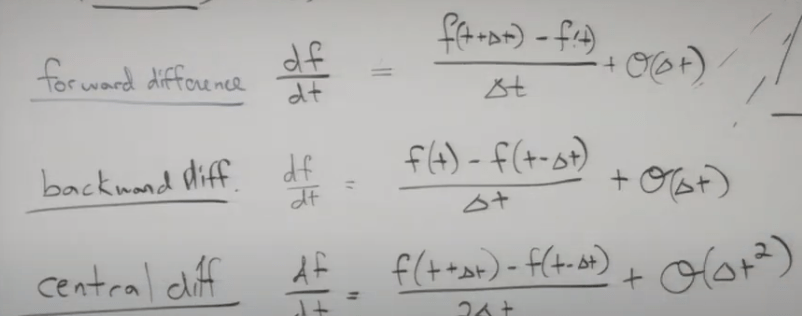
In the same vein, we can compute the second derivative as

Switch gear to integral, this is the famous Riemann integral to compute the area under a irregular shaped line:

How to solve any ODEs?

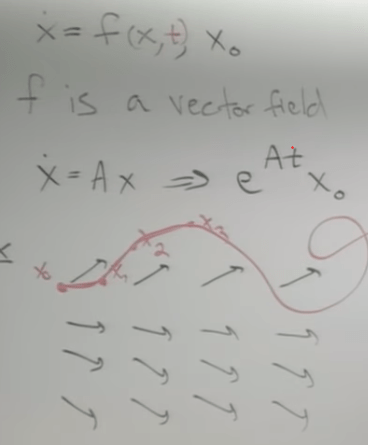
its forward Euler equation, notice its approximate; there is another “implicit” Euler equation,

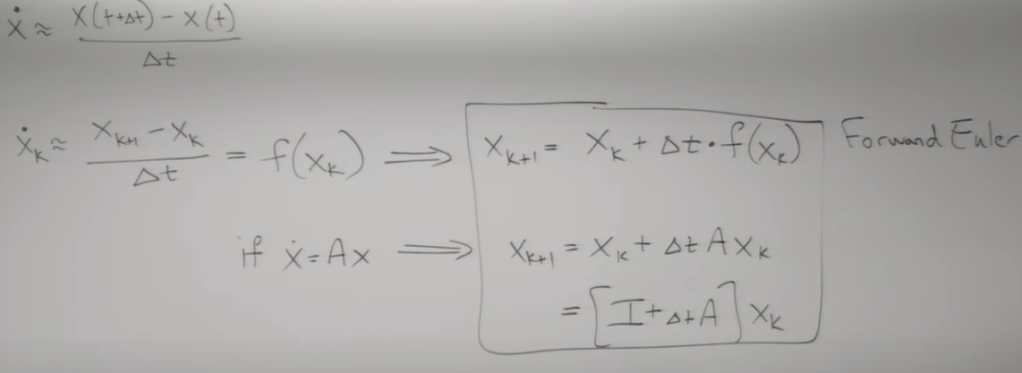
Implicit backward Euler equation

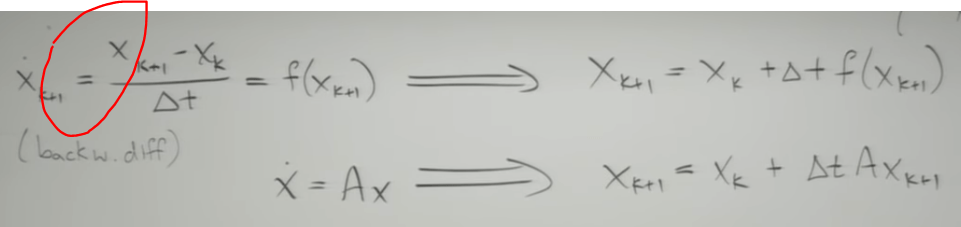
It turns out the implicit approach is more stable. By decreasing the dt, we can make it more accurate. both are similar in terms of accuracy or error terms compared to ode45(Runge-Kutta integration of ODEs).

It can be explained as following

RK approach or ode45 is

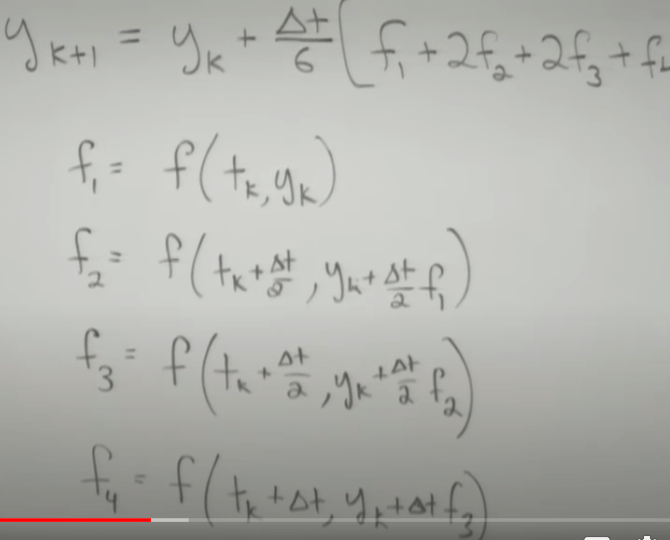
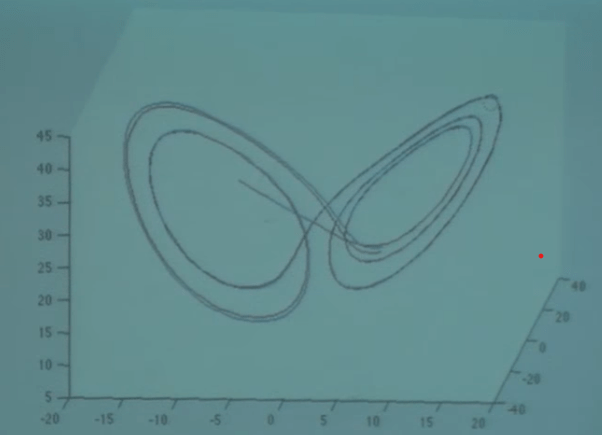
in real world, body motion system could be very chaotic even these numeric integration is hard to solve. One case is Lorenz Equation to describe the Lorenz Tract like butterfly shape.

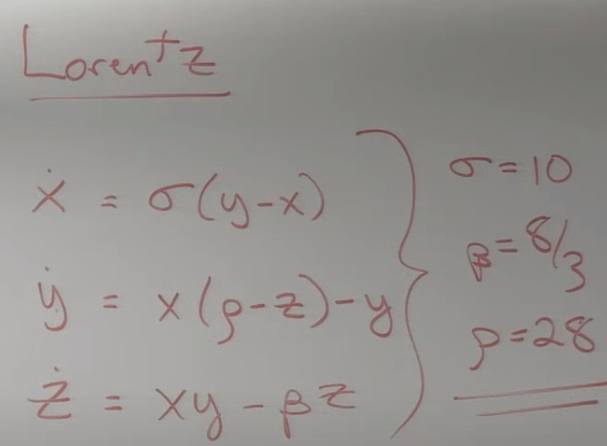
Two particles close with each other at time 0 could depart each other and goes to entirely seperate trails. Code it up and observe it’s mimicking (comparing the step by step function and ode45 directly)