Why on earth did mathematicians invent complex number i? I found the best answer from prof.Herbet Gross, who use a real case in life – simple ODE and everything become sensible.

And we also know that somehow these two solutions are equivalent to cos(x) and sin(x).

Prof. Brunton however approach this by the concept/problem of “roots of unity” to intuitively transform arithmetic thinking into pictorial (polar) description.

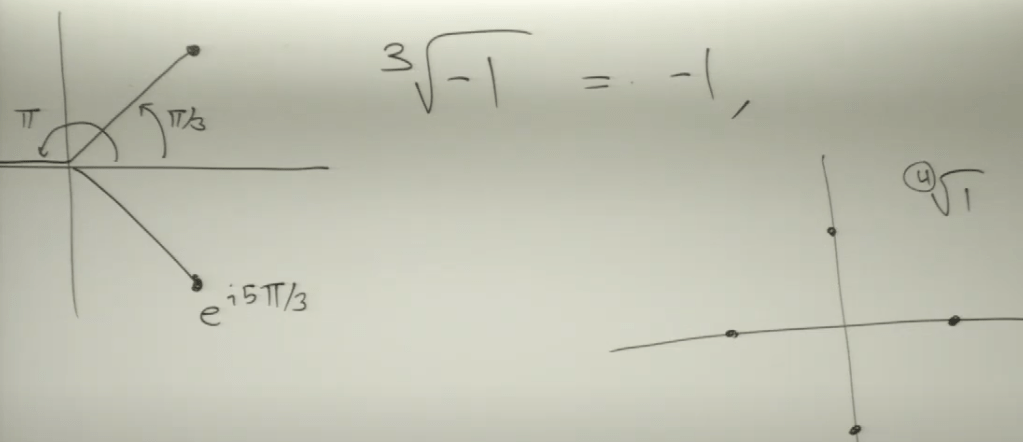
Leading to a generalized expression of any complex or true value z raised to a – a is a rational number (m/n):

So the real part is fixed, while the imaginary part can have multiple values

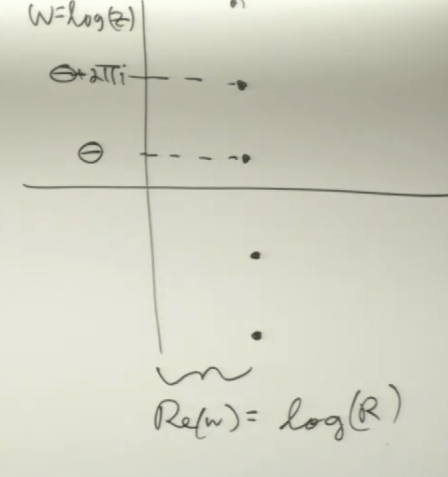
Branch cuts, the concept is to pick from multiple imaginary part values, deem it as the principle.

conservative vector field, it’s analogue to complex system, called analytic function. 1/z when z is 0, is not analytic as it’s singularity. also note that function of z has to be expressed as closed form not simple combination of x and y, for example, z = x – iy is not analytical function f(z).

if f(z) is analytic, then f'(z) must be same regardless of path. Lastly, f is single valued and has finite derivative f’. Hence we get Cauchy-Riemann conditions:

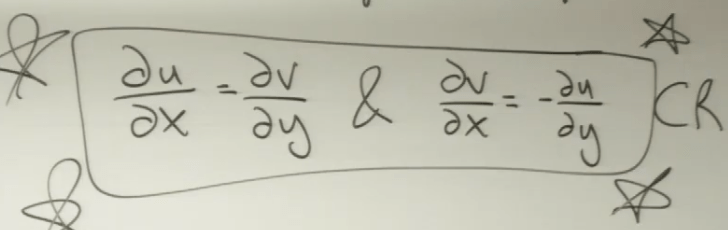
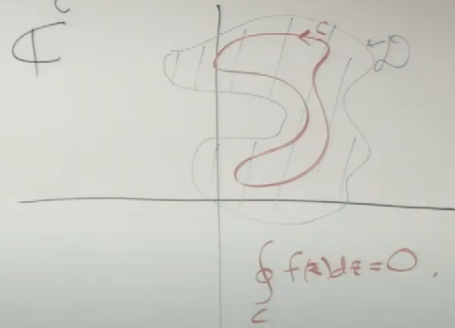
Next, Integration in the complex plane (Cauchy-Goursat Integral Theorem).

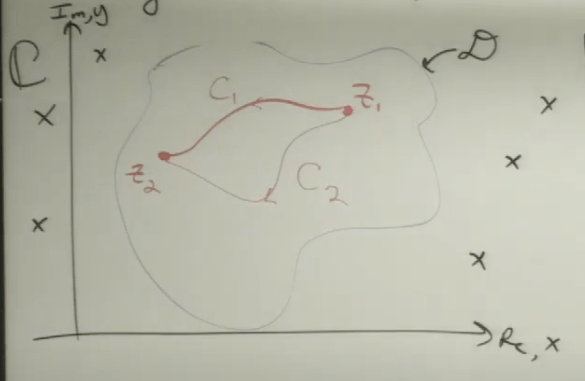
So in above diagram, z1 to z2 agnostic about path. antiintuitive to the 2D that we’re used to.

its’ easy to prove using Green’s theory

To sum, if f(z) is analytic domain D, D is a simple contour area, then the integral of C = f(z)d(z) equals zero.

All polynomials are analytic. For example the case below, when n=-1, it’s special.

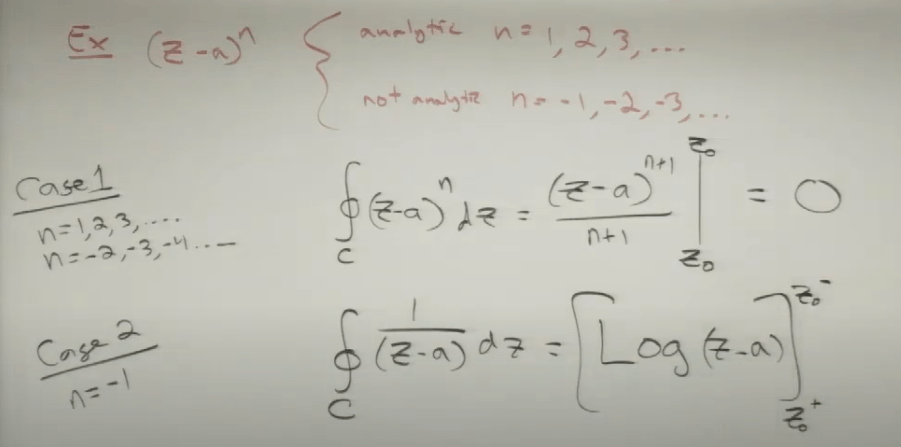
(supplemental on why case2 solution is as above, go back to basics of integrate 1/z in a circular line using parameterization technique:

Here is what prof.Brunton’s two approaches to prove the same

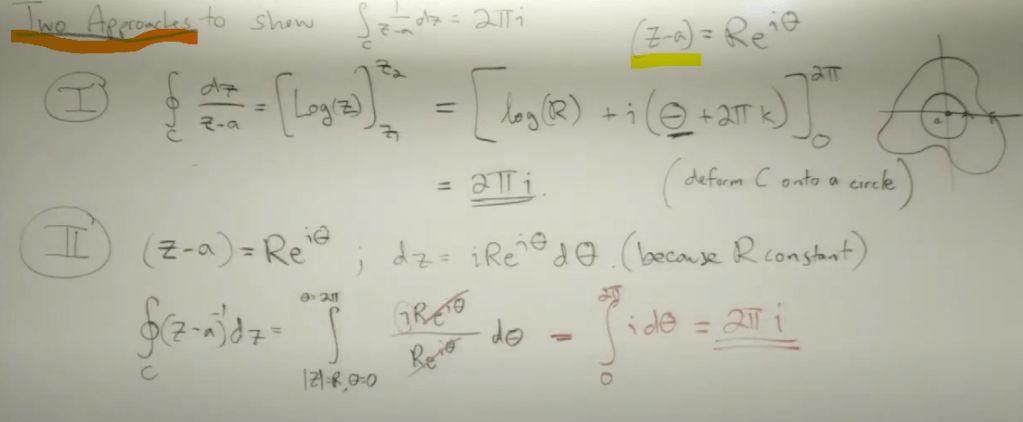
These work is to lead to Cauchy Integral Formula(CIF), which is “If f(z) is analytic inside and on a closed curve C and if the point a in the complex plane and inside the contour C, then:” (Note it’s fixating on the special case (z-a)^n and n=-1 case, then introduce another special case leading to singularity that is a = z, causing denominator to be zero)

It’s powerful to solve lots of integral problems. Feynman vowed to never use integral table, always do it by hand and using this CIF to stick to this practice.

To apply it, what if the f(z) = cos(z), or rewritten as cos(z)/z (a=0), the integral should be 2pie*i*(f(0)) = i2pie. Use programming to check it out:

Ramification: what if f(z) = sin(z), f(z)/z = sin(z)/z, this is actually analytic per Taylor’s series….

In the end, don’t forget all these endeavors are aimed to solve integral problems, particular, Laplace transform and Fourier transform which have profound application in daily life.

Adding on 20230822, I’ve observed that the Jacobian matrix aligns with the Riemann-Cauchy equations during transformation. This suggests that complex numbers not only align with matrix transformations but are identical in nature. In some respects, complex numbers provide a more elegant and concise representation of rotation compared to matrices.