To tackle really complex integral problems, we need to start from ML bound:

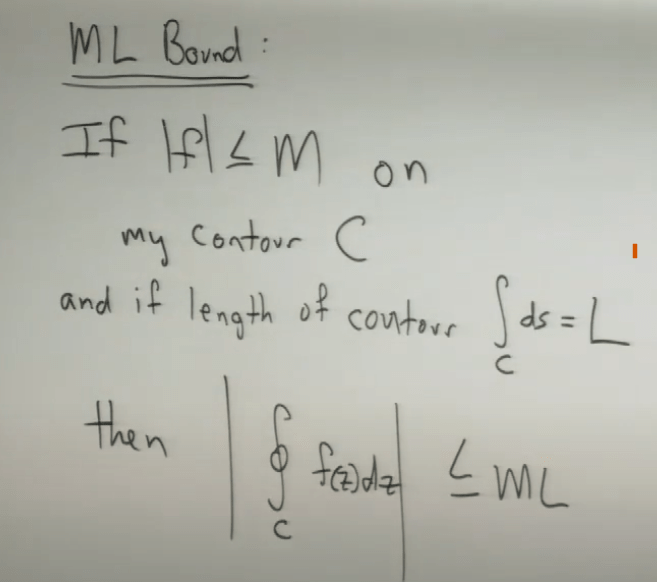
Now let’s try a simple integral function f(z) = 1/(z-1)(z-2) by leveraging the CIF form “f(z)/(z-a)dz”.

Now try to tackler a harder problem, in the same vein, we’ll turn it into a closed contour problem like above.

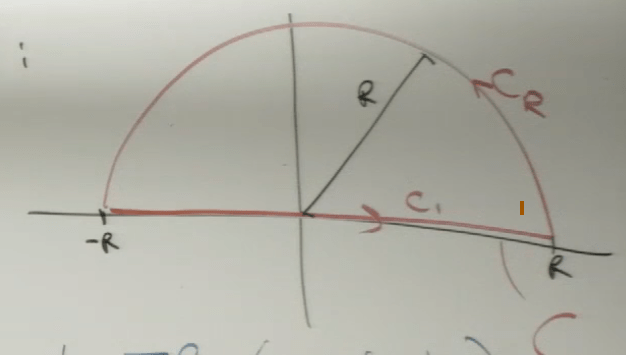
So let the integral aiming to solve equal to I, we can rewrite the form introducing complex variable z below, if we can prove the right part to I is zero, then the problem is converted to calculate integral of 1/(z^4+a^4), which CIF (Cauchy Integral Formula) can come to aid.

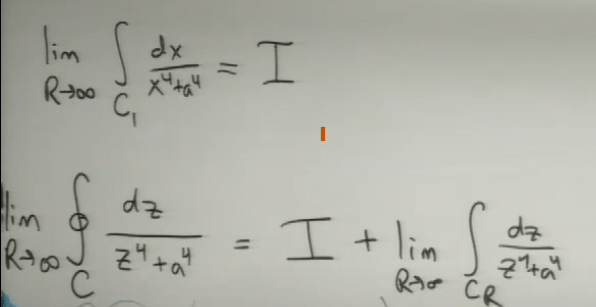
Applying the ML boundary at the very beginning, it’s easy to deduce that this part is 0:

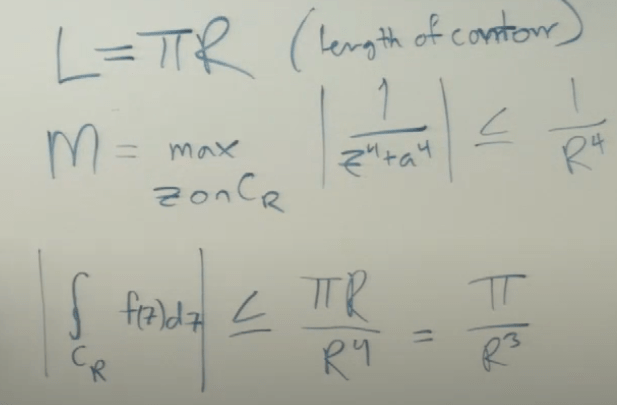
Then applying CIF to solve the complex integral problem, even it’s more complex than the above example, the procedure is exactly same

Hence the solution is

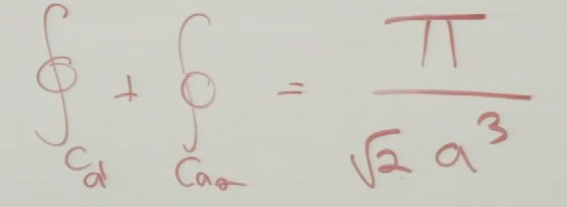
Now try to solve inverse Laplace transform. First of all, why should we be interested in solving such questions as Laplace transform, Fourier transform? it’s for solving differential equations, ode. So Heat equation, frequency domain real world problems can be solved.

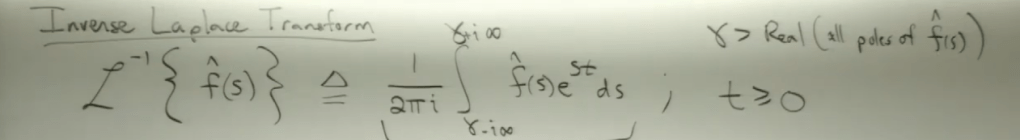
start from f(s) hat = 1/s-a, (it’s related to solving ODE, will expand later on), the inverse Laplace equation can be written as following. Again to solve it we draw the left part a closed contour to tap CIF, as denoted below, CIF helps to figure out the whole circle is e^at, then we need to deduce C+, C- and CR in total is zero, then what we try to solve is exactly equal to CIF of the entire contour, a.k.a. e^at.

The left side D shaped contour has a special name called Bromwich Integral.

To prove, first, C+ and C- by using ML boundary theorem

Then the integral of CR, not possible to use ML bound to work, so we resort to lots of tricks to figure out when R blows up to infinity, it also reduced to zero. The process is omitted here, but in essence, we need to think about intuitively that when s goes to extremely left side, e^st will be extremely small. It also relates to another potential solution – to draw a right-hand D contour. It’s not feasible because as a(the pole) is not within this D part, the whole integral would be 0, so the right curve part is not reduced to zero, we have to compute it, it’s equally difficult to compute the C vertical line itself, hence dead end.

Finally, I need to think further about ds = ? in this polar coordinate system.

from khan academy we know if r = f(theta), the arc length ds can be computed as

so ds=Rdtheta.