As is demonstrated by Sal, prof.Brunton’s version

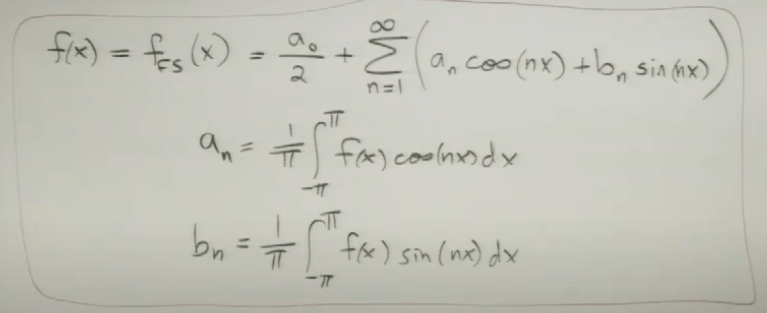
to have a further understanding on transforming f(x) to fFS(x), we need to know definition of two functions are equal:

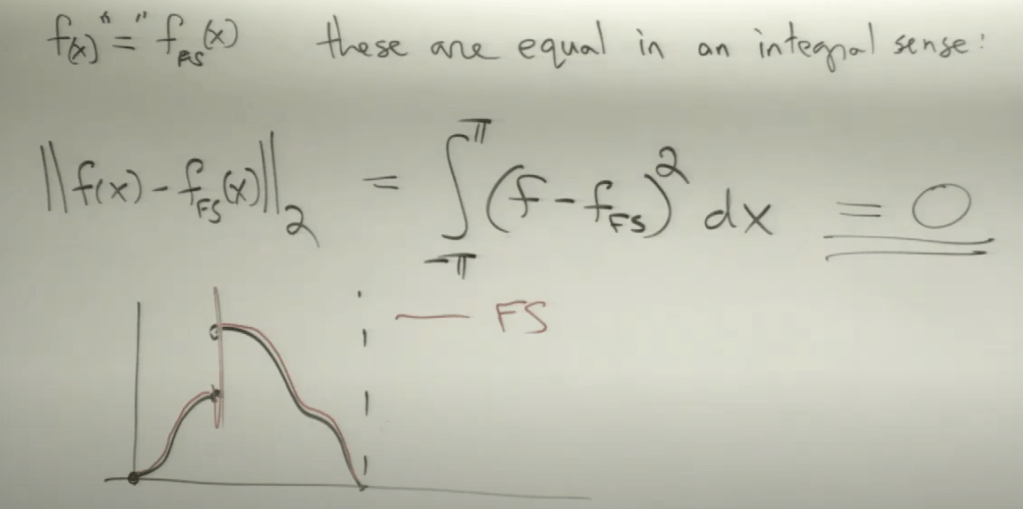
Even there are discontinuities at that cliff point we still claim these two functions are equal per “L2 integral norm”.

Vector space is a foundational concept. The precise mathematical definition is as follows:

To measure the magnitude of vectors, the immediate notion is norm, more accurately inner product space

e.g. Norm of a 3-vector u is

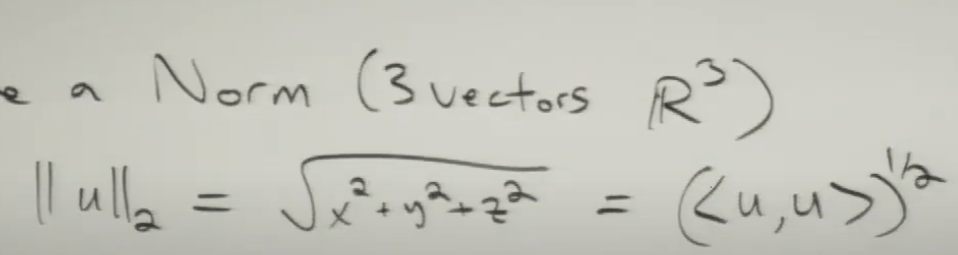
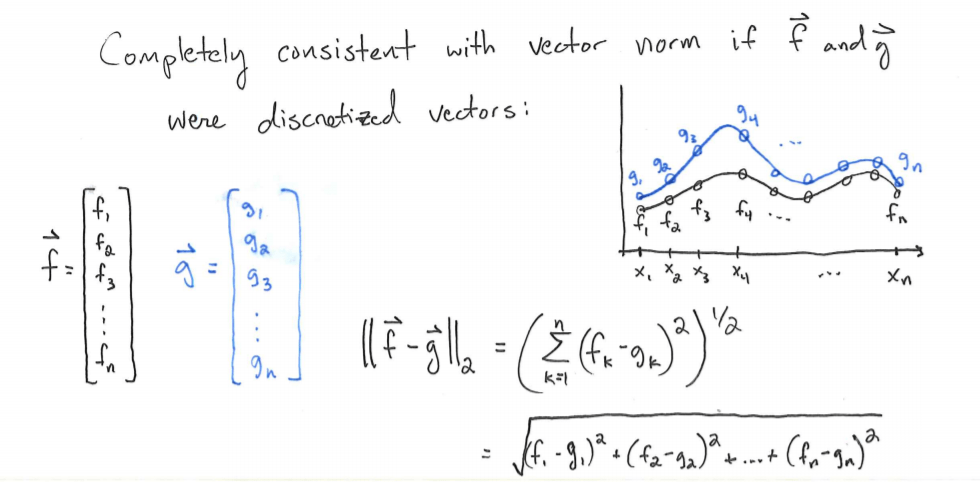
Similar, norm of a function is

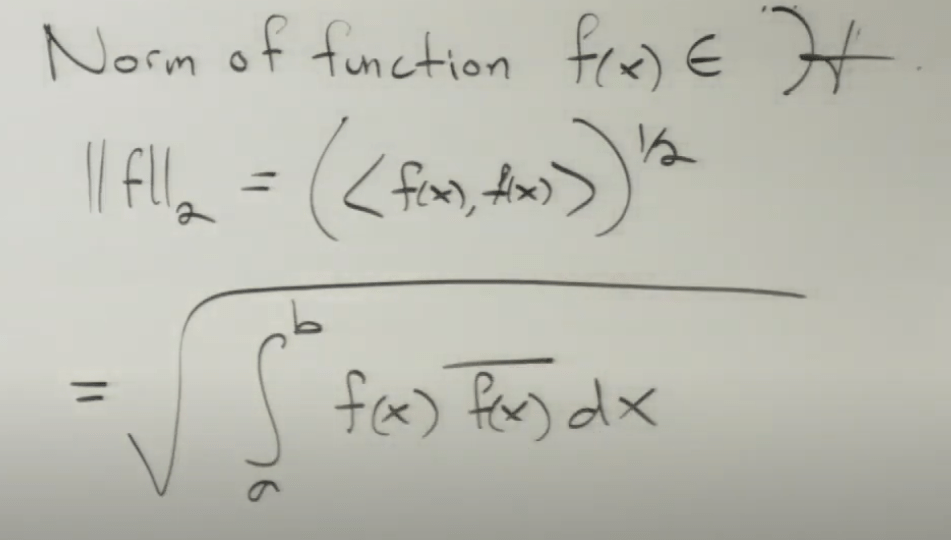
Next, to measure how close two vectors are, we can apply it

To intuitively understand, using the below picture view

Now relates back to Fourier Series, all functions can be fully expressed as below and we can conduct complex dissection algebraically.

Throwing another important condition for further cleaning up – recall Sal took great length to prove the below, this is distinctive and useful feature of sin and cos functions we can make full usage.

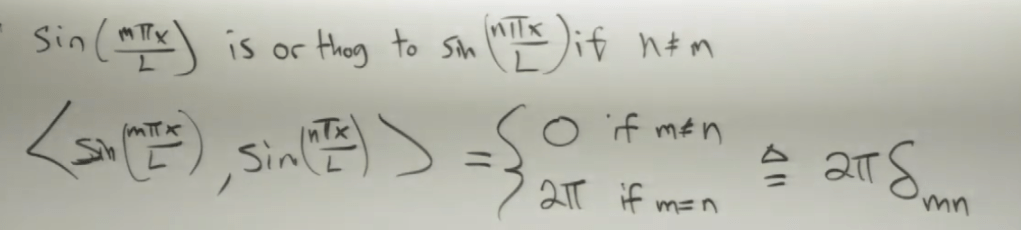
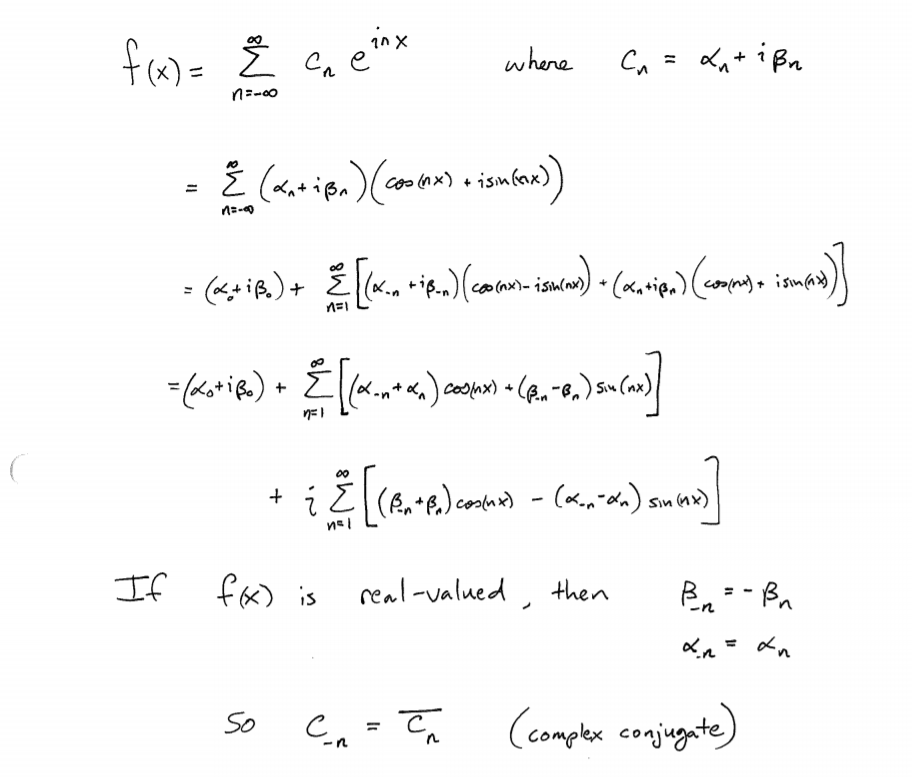
Building more bricks here, we say the set of fais is orthogonal function basis, proved as below:

Throwing another critical building brick – how we understand expression of vectors(functions) in various coordinate systems:

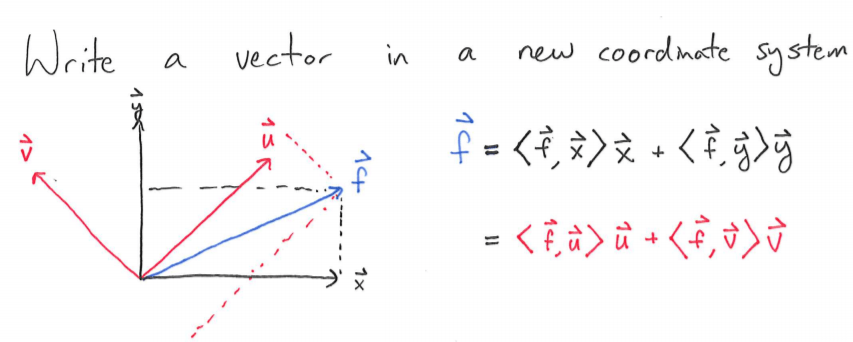
Now it comes naturally that a Fourier Series is just a change of coordinates of a function f(x) into an infinite dimensional orthogonal function space spanned by sines and cosines.

And

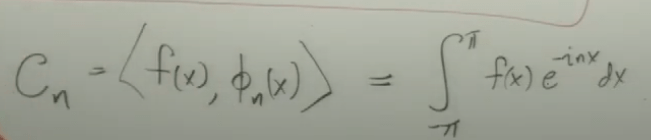
If f(x) is real value function

This looks analogous the the extreme simple form (square wave) Sal deduced, also similar to the numerical integral of heat equation, and analytical function decomposition or separation of variables:

So for any f(x), we can apply Fourier Transform technique to rewrite into coefficients and frequency sin or cos. But why bother this hassle? It turns out to be incredible useful in solving lots of PDE problems by converting to ODE problems.

To make it a more generic form, we define frequency w = npie/L and push the L to infinity, therefore boundary from negative infinity to positive infinity to get the most familiar-looking FT form:

Additional notes to understand “inner product”, which is of a larger category of dot product.

Every vector space(linear space) V, over the Field F with a defined (not necessarily the standard) inner product function is called an Inner Product Space.
If F = R, then it’s a Euclidean space,
if F is made up of complex numbers, it’s called unitary space.