The Fourier coefficient looks exactly same as the frequency domain f(w) hat:

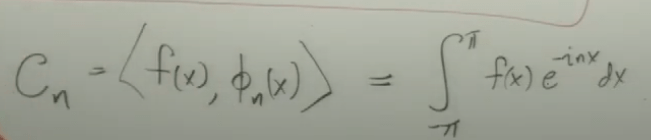
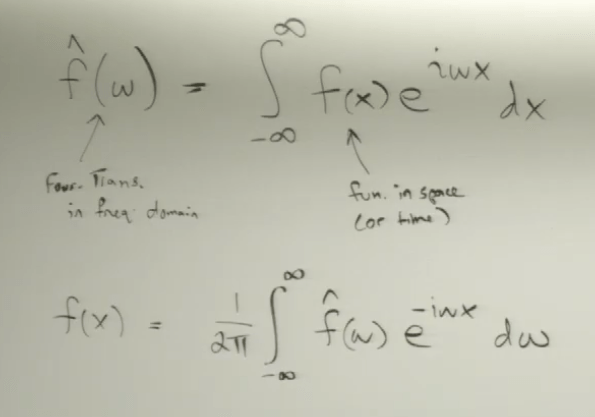
for any f(w) which is a complex valued function, even for real valued f(x), in which case, it’s cos part exists, sin part disappears, there is a magnitude and phase, as denoted above.

Here is a concrete example to transform a normal f(x) into Fourier form:

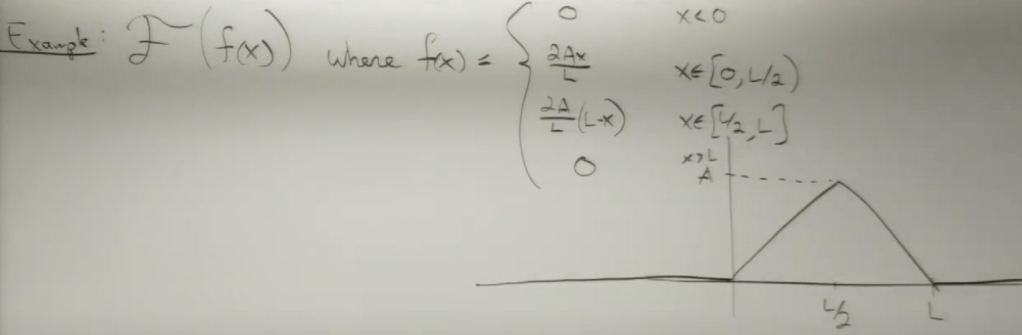
After steps of integral calculation, we got

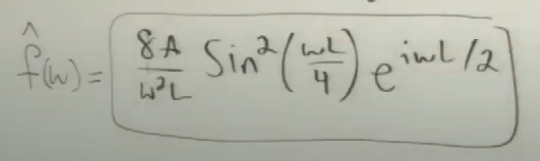
Take it apart to sketch using frequency omega as the x axis

So if you want to know the frequency omega is 2pie/L, it should be of magnitude aobut 4 and phase = Theta = wL/2.

Before expanding on how Fourier Transform help solve PDE problems, we’d like to know the properties of FT:

Lastly we need to use an example to illustrate how FT help reduce PDE problem to ODE problem, a toy example is to pluck a string Utt = c Uxx, then we apply the first important property of FT.

Fourier Transform helps reduce Partial Differential Equations (PDEs) into Ordinary Differential Equations (ODEs) by converting functions of multiple variables into functions of fewer variables. Here’s the intuition and step-by-step explanation of how it works:

We can also Use Laplace Instead of Fourier because Laplace naturally handles exponentially decaying solutions, common in heat conduction problems.

Laplace Transform is great for time-domain problems, where initial conditions are known.

Fourier Transform is better for spatial problems (e.g., infinite domains, periodicity).