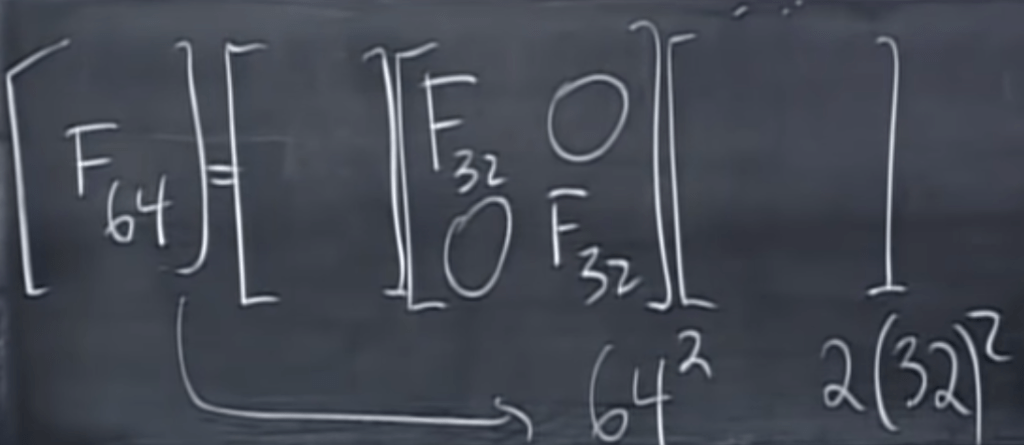Going over Taylor Series first,

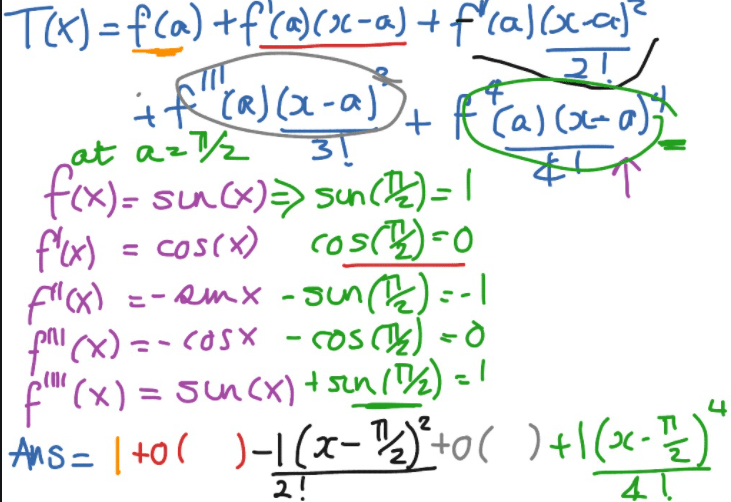
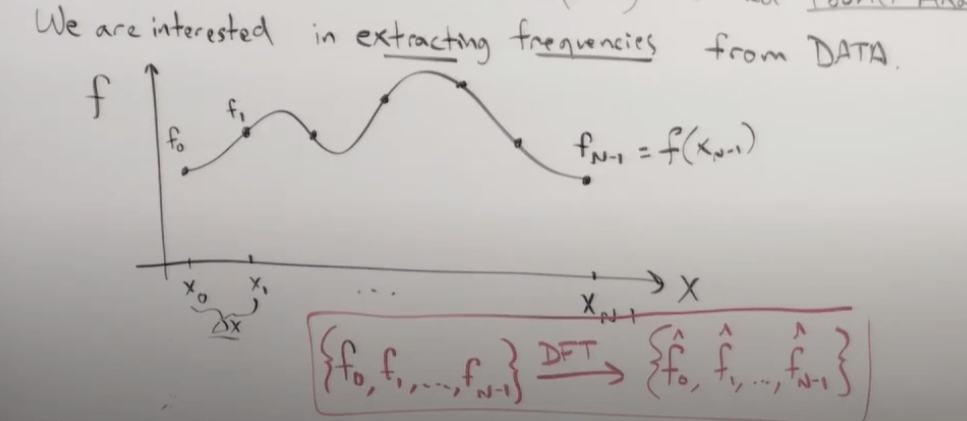
However, instead of non-periodic polynomial functions like y = x^4 – x^2, some functions like sin(x) is not suitable by Taylor series. A better solution would be using sum of sin waves or Fourier Series to represent.

• For local approximations: Taylor series is better.
• For periodic approximations: Fourier series is better.
• For frequency analysis: Fourier Transform is better.

So to generalize given a sets of data (x – f(x)), we want to transform them into set of frequency f (f hat).

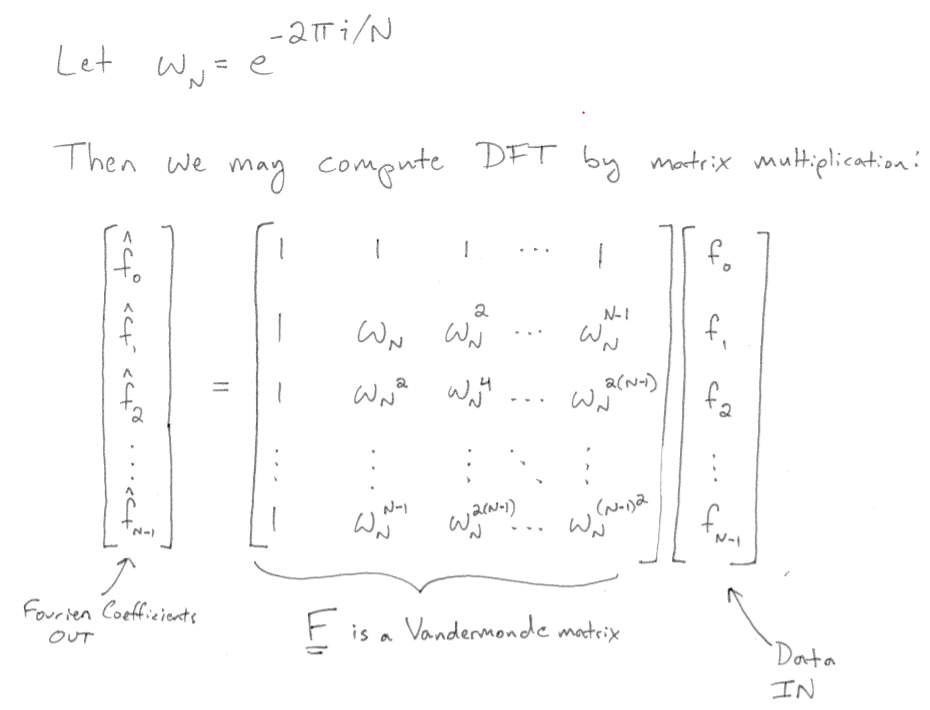
Fast Fourier Transform (FFT) is one of the most important algorithm ever developed.

Now to see the power of FT, let’s add some noise onto a simple synthesize curve

#discrete fourier transforms
dt = 0.001;
t = 0:dt:1;
x = sin(2*pi*50t) + sin(2*pi*120*t) #construct 50hz and 120hz mixed signal curve
figure
N = length(t)
Y = fft(x, N)
PSD = Y.*conj(Y)/N #power spectrum or how much power is in each freq
freq = 1/(dt*N)*(0:N)
L = 1: floor(N/2);
plot(freq(L), PSD(L))
#add random noise
y = x + 2.5*randn(size(t))

It makes much easier to filter out the noise by adding a threshold of PSD, then apply inverse FT to get the original wave form.

Reference MIT professor Dr.Strang 18.06 on complex matrix and Fast Fourier Transform.

complex matrix is special and need to adjust in some ways: first. the length cannot be simply calculated as Z^TZ as in real matrixes, instead, you need to take conjugate first then transpose it to multiply to itself.

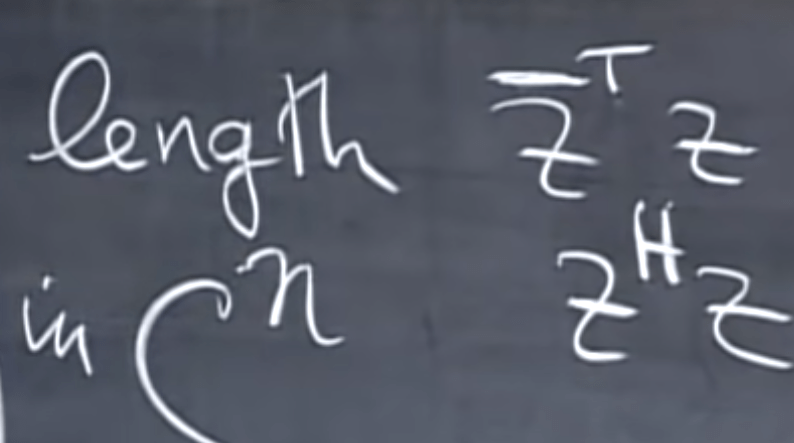
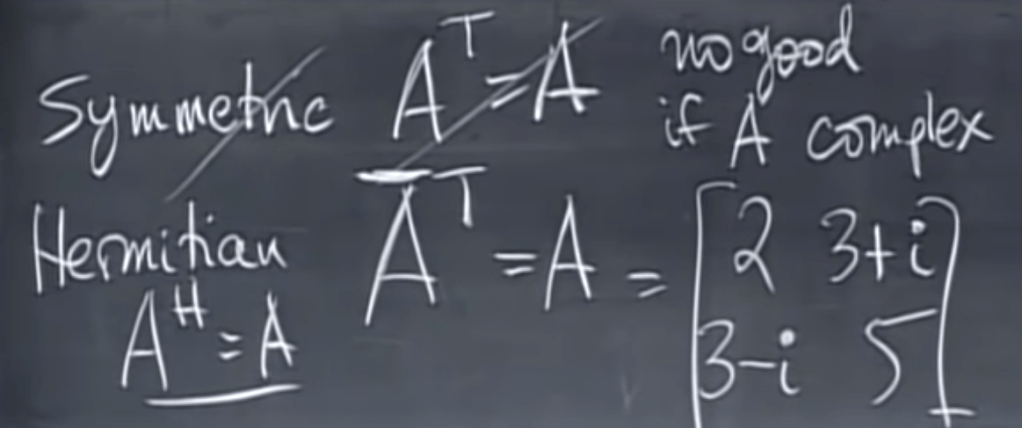
Note Hermitian is replacing symmetric here in complex number’s world. And instead of orthonormal, use the word unitary. Fourier matrix is the most famous complex matrix. To learn that, first look at the below matrix in which w is complex number.

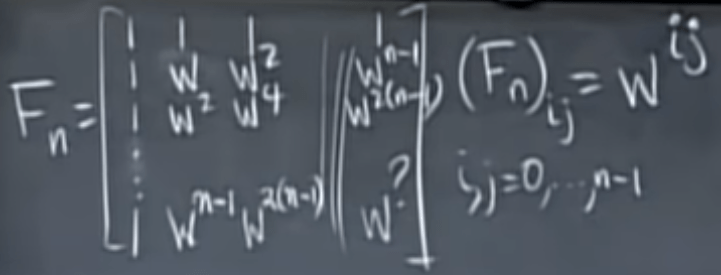
also w has the following feature

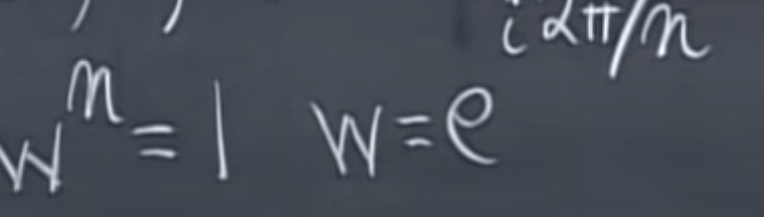
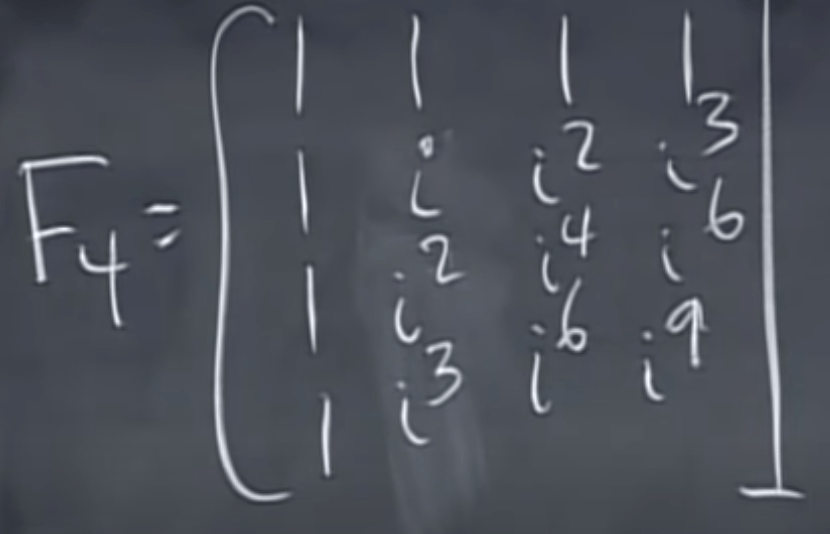
So why do we look into this squared filling matrix, there is a beautiful feature in it that Gauss saw and Fourier himself at that time didn’t take notice(per Dr.Strang)

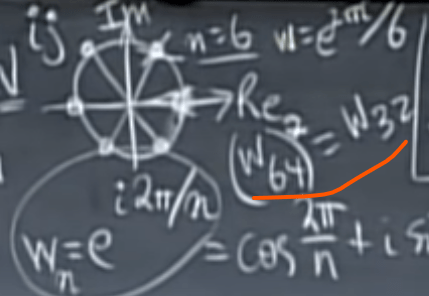
So leveraging it, it’s possible to reduce high dimensional computation to much lower n/2 computation by