in ODE we get fair familiar with the concept of characteristic equations, and eigen value, eigen vectors.

for equations with repeated roots, the general solution is

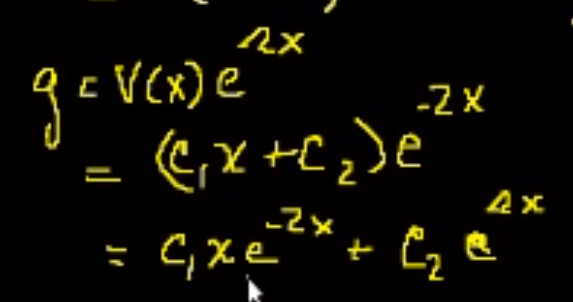
For example

Undetermined coefficient for solving non-homogeneous equations. In mathematics, the method of undetermined coefficients is an approach to finding a particular solution to certain nonhomogeneous ordinary differential equations and recurrence relations.

Then move on to Laplace transform.

starts with integration by parts:

Laplace(1) = 1/s

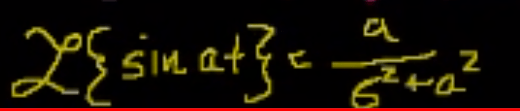
Why Laplace transform is useful in solving differential equations?

Because it has this unique property, it turns derivative into multiplication.

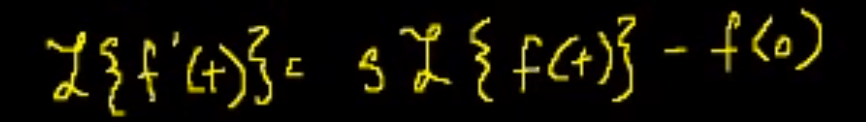
Another important property, because

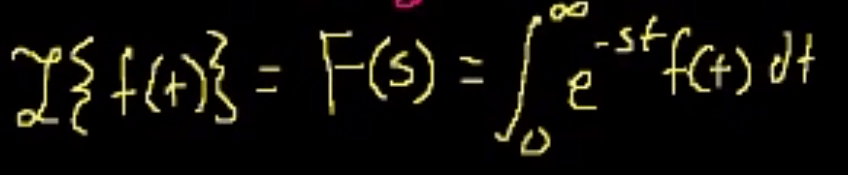
so similary

for example

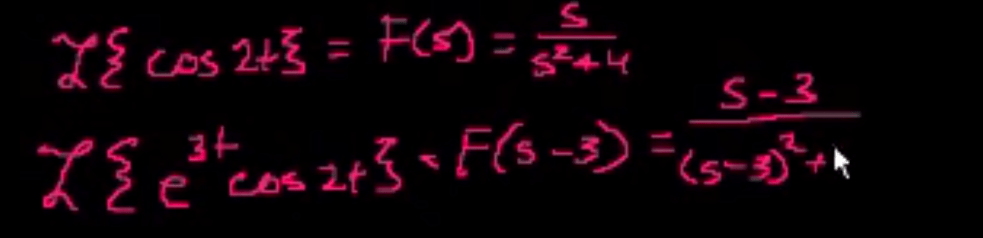
L(1) = 1/s, L(t) = 1/s^2, L(t^n) = ? there is a pattern.

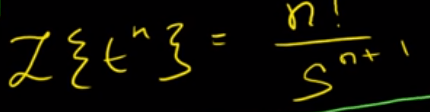
unit step function is defined as discontinious step up curve

Note to differentiate it from

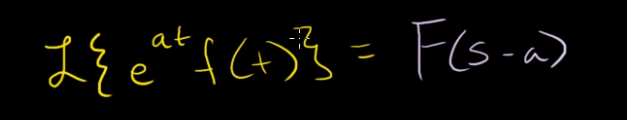
With these tools at hand, we can try figuring out inverse Laplace transform.

Dirac Delta Function:

We define integral of this Dirac Delta function

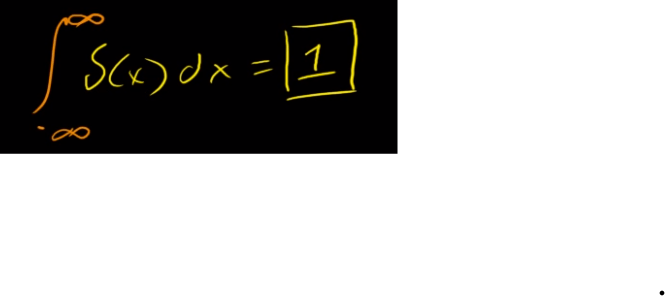
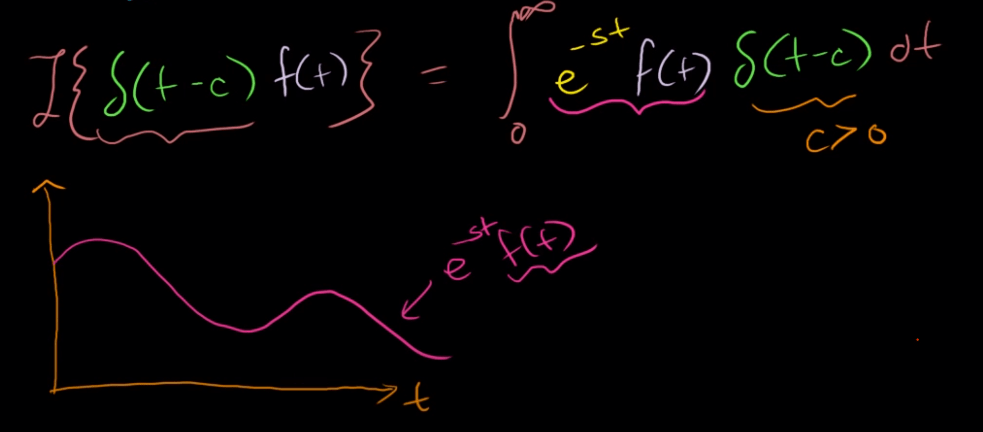
Going through all these troubles of Laplace Transform eventually aid powerfully to solving DEs.

In essence, we can freely convert between frequency domain and time/space domain to sort out complex DE and also manipulate frequency part a.k.a in Fourier Transform to filter out noise or compress images.

Remember this important one

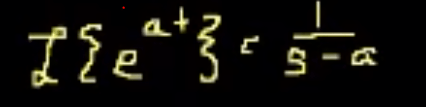
Move on to the final topic – convolution integral. Between two functions/vectors, we can do cross product, dot product, now it’s convolution, what’s the meaning of it, according to wiki:

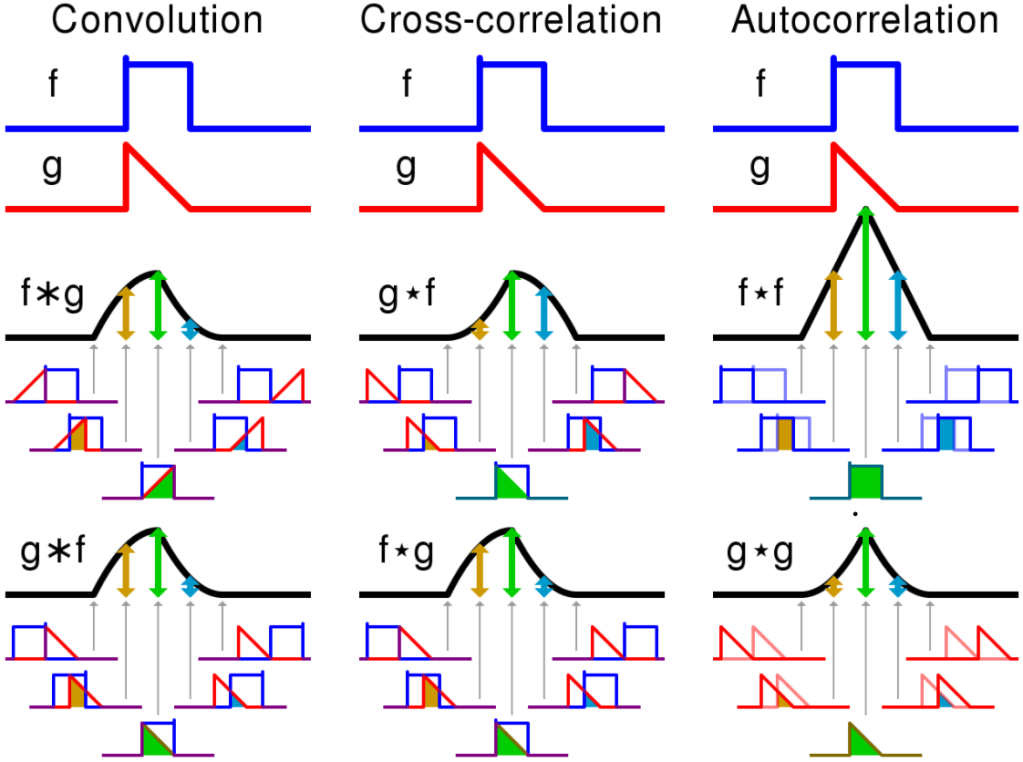
Convolution Integral is defined as

for example to convolute sin(t) and cos(t), we get

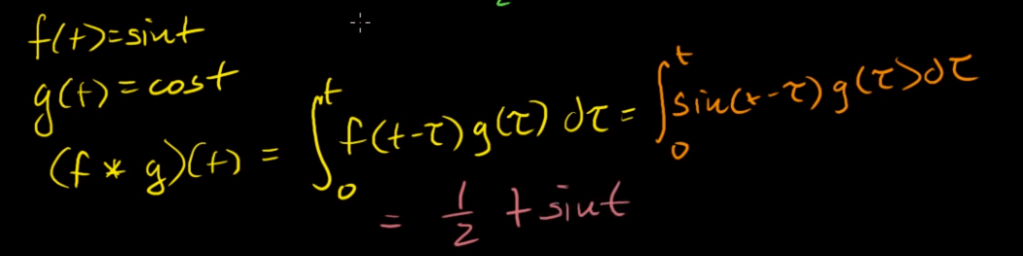
Convolution theorem as applied to Laplace Transform

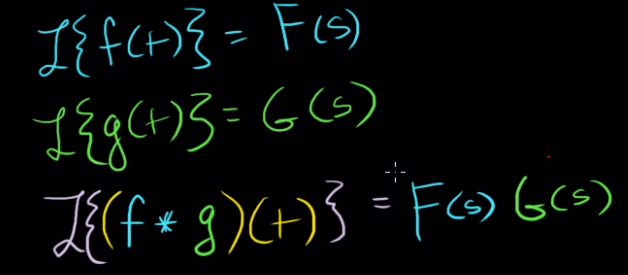
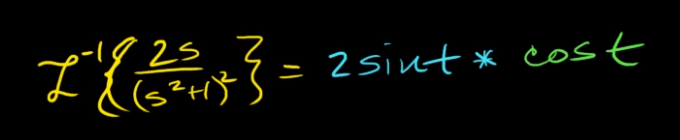
now to apply this convolution theorem to solve an initial value problem.

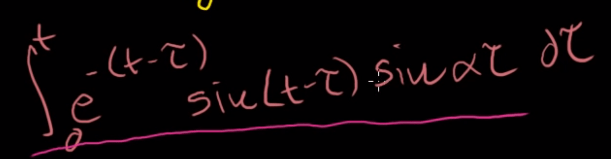
Then we go back to the mechanical engineering class problem I came across: