Semantic or document similarity is of great interest for me. There are various metrics to measure so I’d take a deep dive into it first.
In linear algebra, “norm” is used to define the distance between vectors. L1-Norm is also called Manhattan or taxicab distance, which take the practical distance, for example (3,4)’s norm = 3+4 =7. L2-Norm is more commonly used it’s the Euclid distance in two dimensional space.
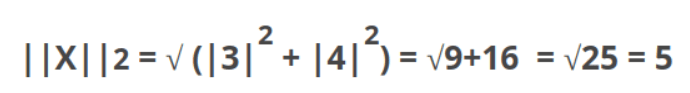
It’s worth noting that above two example, we are measuring the distance or magnitude from a vector to the origin (0,0). What is we need to measure distance between two vectors? If we take the first step of substracting vector2 from vector 1 (v1-v2), forming a new vector, then calculate L2-Norm of this new vector, the magnitude of (v2-v1) is the distance between the two.
To be more generic, we need to introduce the concept of Hilbert Space:
A Hilbert space is a vector space equipped with an inner product, an operation that allows defining lengths and angles. Furthermore, Hilbert spaces are complete, which means that there are enough limits in the space to allow the techniques of calculus to be used. (wiki)
In this space an L2 norm of a vector composed of three scalar values is

Note it’s the square root of inner product of the vector itself. to get further insight on magnitude/norm of functions, then to compare distance of functions my previous blog.

This description of similarity is also called cosine similarity, consistent with Pearson Correlation. Also referable to the following equation in comparison to Jaccid similarity:

Why it’s necessary to understand metrics of similarity and then norm/magnitude of vectors because documents can be digitized and converted to vectors too.
Now we set ready to deploy document similarity algorithm:
The gist of this approach is to digitize each word in the document, i.e. vectorize the document. To offset the frequently-used stop words such as “all, is, are…”, a common approach is TF-IDF(term frequency- Inverse Document Frequency). TF-IDF is intuitively straightforward, illustrated as following:
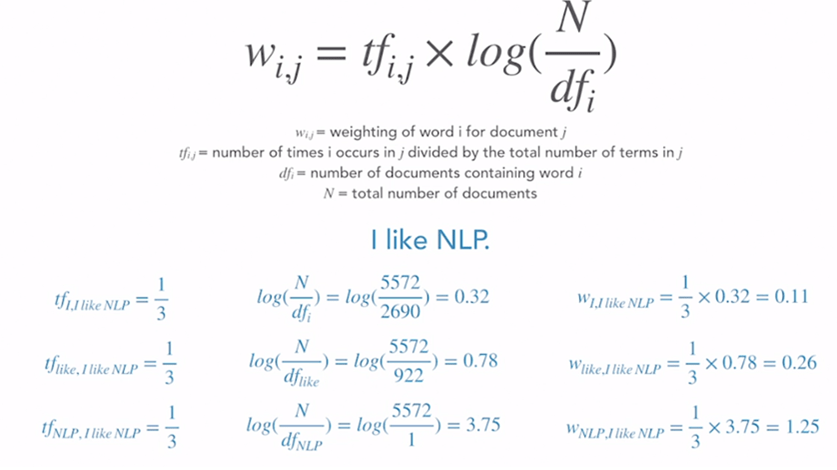
After vectoring documents for the whole universe, we can compute the cosine similarity:
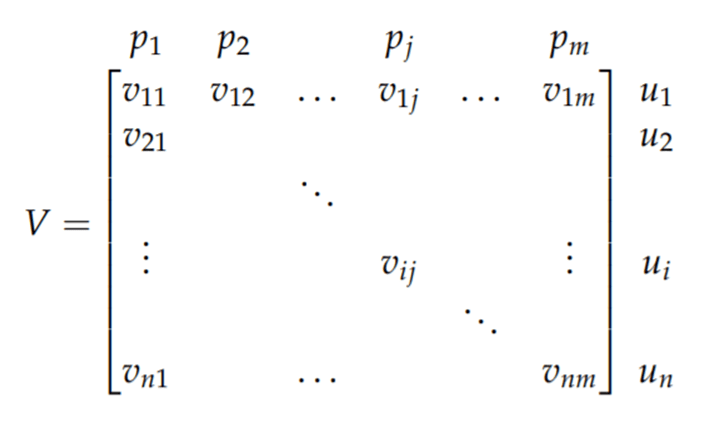
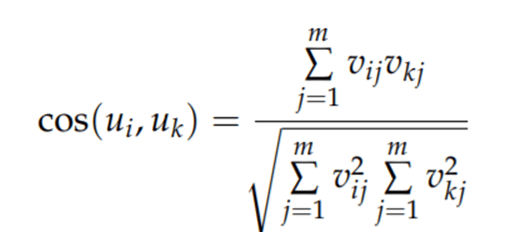
In this case, the target document(to-be-compared document) can be a combination of our picked keyword strings. Then we apply each company’s “management discussion” session vector to find similarity to this target document, get a score and rank them top down.
There are open package to perform this primitive NLP. This data science blog (https://towardsdatascience.com/natural-language-processing-feature-engineering-using-tf-idf-e8b9d00e7e76) provides a clear and neat explanation.
So finally I applied this method using business description of 117 “space” company sifted out via industry classification, then use LSA + human input to come up with a bag of “relevant keywords”. The whole script is documented here.
# Similarity Metric
bd.loc[bd.Id == 'tocompare', 'ff_bus_desc_ext'] = 'aerospace space satellite orbital suborbital space exploration space shuttle launch vehicle spaceflight geospatial rocket spaceship space travel spacecraft'
import nltk
from nltk.corpus import stopwords
from wordcloud import WordCloud ,STOPWORDS
from nltk.stem import WordNetLemmatizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
from sklearn.svm import SVC
from nltk.tokenize import word_tokenize
import re
import warnings
warnings.filterwarnings("ignore")
stop_words_nltk = stopwords.words('english')
wordnet_lemmatizer = WordNetLemmatizer()
# Re-add the additional stop words since we are recreating the document-term matrix
add_stop_words = ['like', 'im', 'know', 'just', 'dont', 'thats', 'right', 'people', 'youre', 'got', 'gonna', 'time', 'think', 'yeah', 'said', 'world','company','going', 'customer','demand','market','may','also','system','cost','year','business','including','service','could','product','industry', 'believe','think','continue']
stop_words = set(stop_words_nltk + add_stop_words)
len(stop_words)
def process_text(text):
text = text.lower().replace('\n',' ').replace('\r','').strip()
text = re.sub(' +', ' ', text)
text = re.sub(r'[^\w\s]',' ',text) # \w is any word-class character (alphanumeric as Jonathan clarifies).the beginning of a line (^) followed by either a single alphanumeric character or an asterisk \s is whitespace characters
word_tokens = word_tokenize(text)
stemmed_sentence = [wordnet_lemmatizer.lemmatize(w) for w in word_tokens]
filtered_sentence = [w for w in word_tokens if not w in stop_words]
longwords = [w for w in filtered_sentence if len(w) > 1]
text = " ".join(longwords)
return text
bd['Text_parsed'] = bd['ff_bus_desc_ext'].apply(process_text)
#LSA
from sklearn.feature_extraction.text import TfidfVectorizer
len(stop_words)
vectorizer = TfidfVectorizer(stop_words=stop_words, smooth_idf=True)
# tokenization
tokenized_doc = bd['Text_parsed'].fillna('').apply(lambda x: x.split())
utext = pd.Series(bd.Text_parsed.unique())
X = vectorizer.fit_transform(utext)
X.shape
dictionary = vectorizer.get_feature_names()
len(dictionary)
from sklearn.decomposition import TruncatedSVD
# SVD represent documents and terms in vectors
svd_model = TruncatedSVD(n_components=3, algorithm='randomized', n_iter=100, random_state=122)
lsa = svd_model.fit_transform(X)
#check the concepts/features
pd.options.display.float_format = '{:,.16f}'.format
topic_encoded_df = pd.DataFrame(lsa, columns = ["topic_1", "topic_2", "topic_3", ])
topic_encoded_df["documents"] = bd['ff_bus_desc_ext']
docview = topic_encoded_df[["documents", "topic_1", "topic_2","topic_3", ]]
docview.head()
sortdoc = docview.sort_values('topic_1', ascending=False).reset_index()
# sortdoc = docview.sort_values('topic_2', ascending=False).reset_index()
sortdoc.head(2)
sortdoc['documents'][1][:2]
encoding_matrix = pd.DataFrame(svd_model.components_, index = ["topic_1","topic_2","topic_3", ], columns = (dictionary)).T
encoding_matrix
encoding_matrix.sort_values(['topic_1'],ascending=False).head(20)
encoding_matrix.sort_values(['topic_2'],ascending=False).head(20)
encoding_matrix.sort_values(['topic_3'],ascending=False).head(20)
#taggeddocument
from tqdm import tqdm
tqdm.pandas(desc="progress-bar")
from gensim.models import Doc2Vec
from sklearn import utils
import gensim
from gensim.models.doc2vec import TaggedDocument
import re
data = bd['Text_parsed']
tagged_data = [TaggedDocument(words=word_tokenize(_d.lower()), tags=[str(i)]) for i, _d in enumerate(data)]
max_epochs = 100
vec_size = 200
alpha = 0.025
model = Doc2Vec(vector_size=vec_size,
alpha=alpha,
min_alpha=0.00025,
min_count=1,
dm =0)
model.build_vocab(tagged_data)
for epoch in range(max_epochs):
print('iteration {0}'.format(epoch))
model.train(tagged_data,
total_examples=model.corpus_count,
epochs=15)
# decrease the learning rate
model.alpha -= 0.0002
# fix the learning rate, no decay
model.min_alpha = model.alpha
# model.save("d2v.model")
# print("Model Saved")
# model= Doc2Vec.load("d2v.model")
from gensim.models.doc2vec import Doc2Vec
# to find most similar doc using tags
similar_doc = model.docvecs.most_similar(0,topn=120)
print(similar_doc)
len(similar_doc)
type(similar_doc)
docdf_ = pd.DataFrame(dict(similar_doc),index=[1])
docdf = docdf_.transpose()
indexlist = [int(x) for x in docdf.index]
docdf.index = indexlist
bd.index
final = bd.join(docdf)
final.to_csv('space exposure rank_test.csv')
test = final[final.index == 1]
bd[bd.index == 1]
test['ff_bus_desc_ext'].values
#to find the vector of a document which is not in training data
test_data = word_tokenize("defense solution aircraft aerospace security system space aviation communication satellite equipment mobile broadband government network data based media sky intelligence mission cyber airborne cubic missile combat aeronautics".lower())
v1 = model.infer_vector(test_data)
print("V1_infer", v1)
model.docvecs.most_similar([v1])