Naive Bayes theory, in essence, is about finding the probability of a label given some observed features, which we can write as P(L | features). To understand it, let’s use a practical example: say, on a campus, 60% are boys, they all wear pants, the rest – 40%- are girls, and girls have 50% possibility they wear pants, if you pick anybody blindly, what’s the chance of he/she is wearing pants?
easy and straightforward, = U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)
the question can be altered to “among the whole group of people wearing pants, what’s the chance that it is a girl?”
this looks daunting at first glance, but provided the first easy question that we have answered of, it’s easy to just put the part of U * P(Girl) * P(Pants|Girl) on the nominator, and divide it by the whole probability: U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] => P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
deduce it to a general form:
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
note p(B/A) is a conditional probability, meaning it is the probability of A, conditioned on B, or vice versa.
Peter Norvig wrote a book on AI, an example in this book is about how to apply Bayes to correct spelling mistakes when we type a searching word. it can be transformed into Bayes probability symbol as
P(B|A) P(guessing the word|actual wrong word she entered)

visual illustration makes it easier to understand:

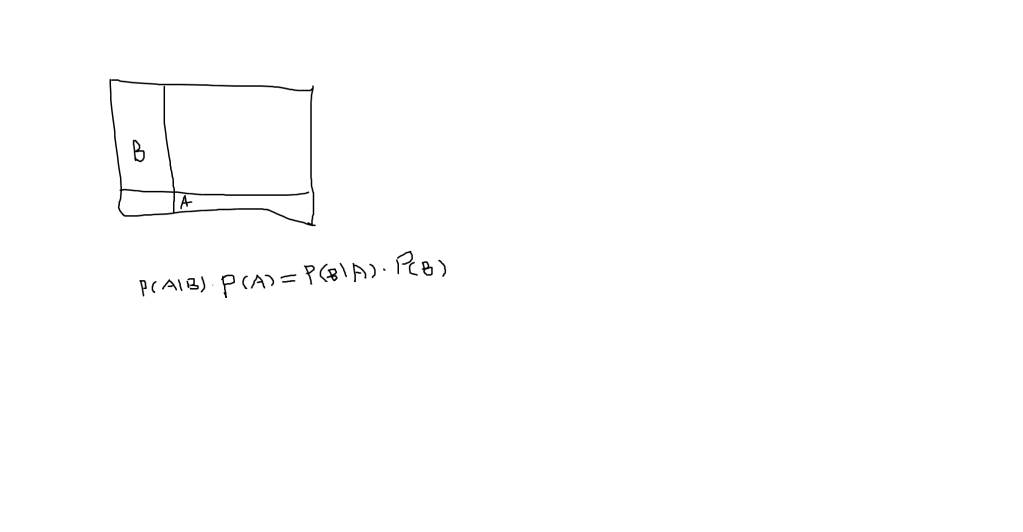
Specifically to the usable algos, there are Gaussian Naive Bayes, the assumption of which is that data from each label is drawn from a simple Gaussian distribution, and  Multinomial Naive Bayes. The multinomial distribution describes the probability of observing counts among a number of categories, and thus multinomial naive Bayes is most appropriate for features that represent counts or count rates. One of its applications is in text classification.

Now learning from Dan Jurafsky at Standford, I expand my understandin of Naive Bayes on NLP. The goal is to figure out the probability of a document being classified based on a particular document

Making it a classifier/function/algorithm

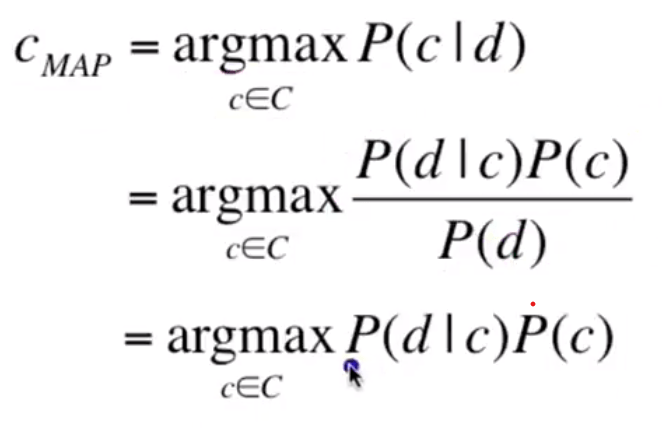
Now if we represent a document by a bag of words, denoted by frequency, the problem can be redefined as below, and certainly we need to make some naive assumptions that the position doesn’t matter and different features x1 to xn are independent given a class.

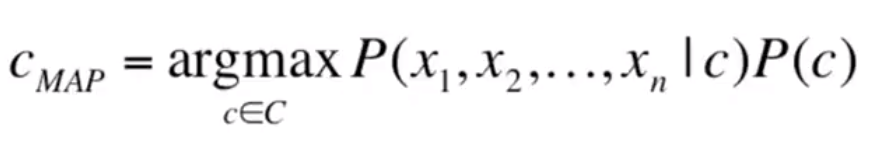
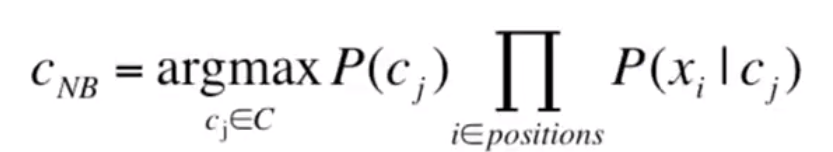
In actual practice, we need to use Laplace (add-1) smoothing to deal with the situation a word never showed up in test data. It’s usage or relationship in language modeling can be illustrated with a worked example:

So for the 5th document we should choose it to be classfied as chinese per Naive Bayes calcultion.

In sum, Naïve Bayes model is very fast, robust, good in domains with many equally important features, it’s generative model, but not as accurate compared to discriminative models.