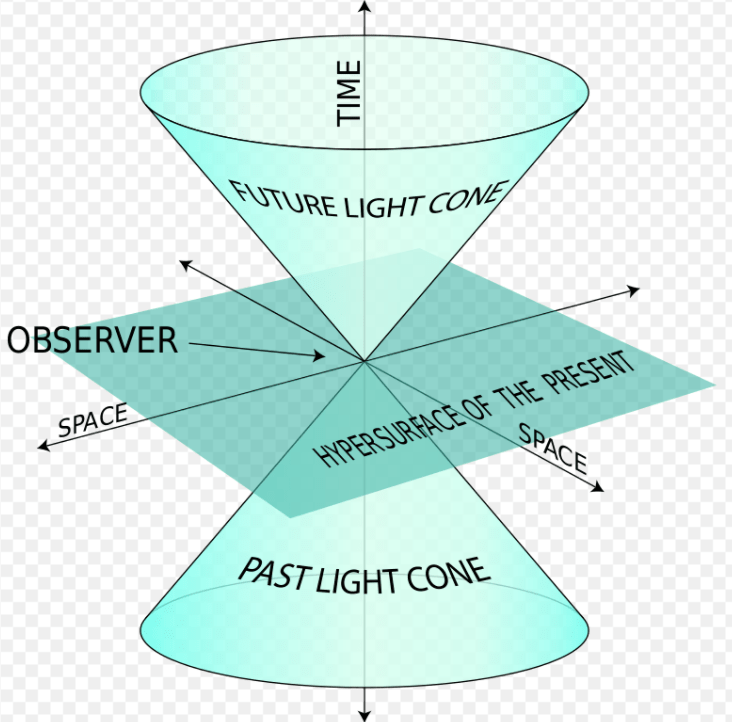
Thanks to Prof.Tadashi Tokieda I have a new level of understanding about the importance in picturing math. It’s also related to understanding special relativity using Minkowski Geometry or Minkowski Space, to the question Prof. Robert de Mello Koch when he asked if one can observe any particle for him. The answer is not sure. He stresses the importance of using the concept of “field” (where and when). Hence if a particle locates out of the spacetime cone, one can not directly detect it.

The following three circle cross each other forming common chords in between, question is whether the three always meets at the center single pt? answer is yes, and question is why?

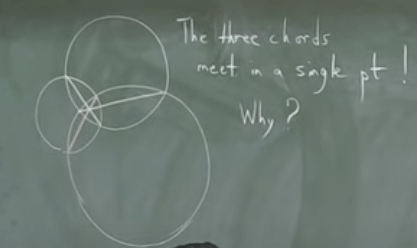
It’s not that easy to prove, but what if we deem the circle in 3D space as spheres?

It’s intuitive to see that three balls form a gut in center, these guts flow to one center pt. QED.

On the other hand, in special relativity we need the tool of Minkowski Geometry. The ground base of this geometry is set on the following equation is absolute in whichever inertial sytems:

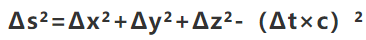
(need to apply Lorentz Transformation to prove it later on…)

Euclid Geometry, which we all are quite familiar is based on the following equation is absolute in which every systems:

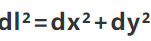
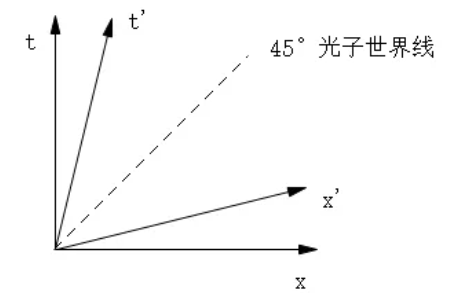
This is the key difference between Minkowski and Euclid Geometry. If we plug in c as a unit, the format is reduced and hence the in spacetime graph, the light line is 45 degree.

Drawing Minkowski geometry picture can help us think of lots of difficult problems such as “concurrent lightening at the head and tail of a running train”:

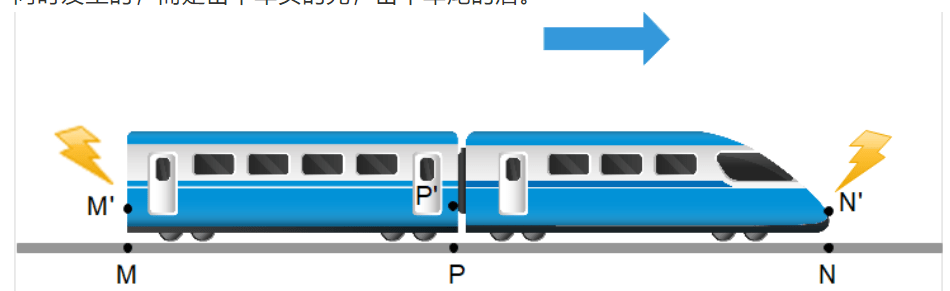
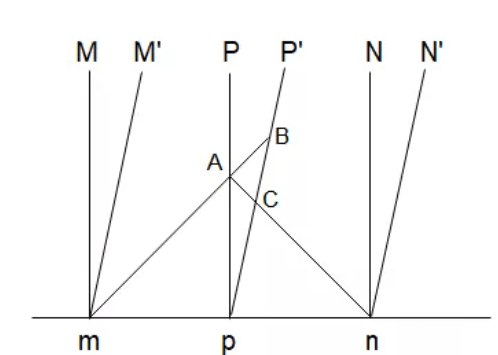
From the view of a person on the ground, she see the lightening happened concurrently at A, while fro the view of a person in the middle of the train, light from the head car comes in at time C, and then she can see the light from the end car come in later at time B.

Now we try to draw both axises (ground and person on the train) to analyze the problem:

Lorenz equation is needed to help draw:

Using this pictorial double axises system, we can easily understand Einstein’s “extended time contracted ruler”.

To start, we need to know to calculate length in Minkowski space:

Hence in a world where particle run at light speed, there is no length, because it’s located on the 45 degree line, meaning deltat = deltax, hence S=0.

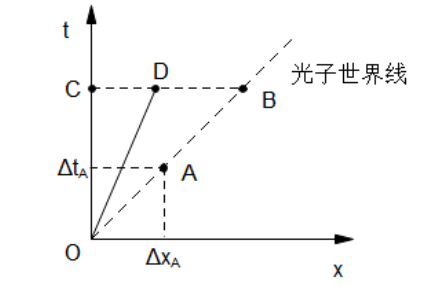
However, in above graph, the length comparison would be OC > OD > OB, counterintuitive but correct.

Now if there is a ruler, it evenly stays at origin y axis is same as t as it doesn’t move, length oa distributes on x axis, since there are Minkowski axises drawn here too, one can see the length there is ob, ob is less than oa. QED.

Now take another angle, let’s draw the line with identical distance say 2 to the origin. In Euclid Geometry it’s a circle with radius of 2; however in Minkowski Geometry, let’s apply the formula

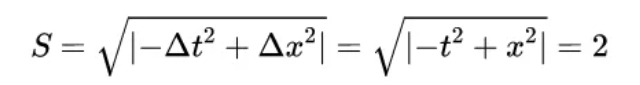
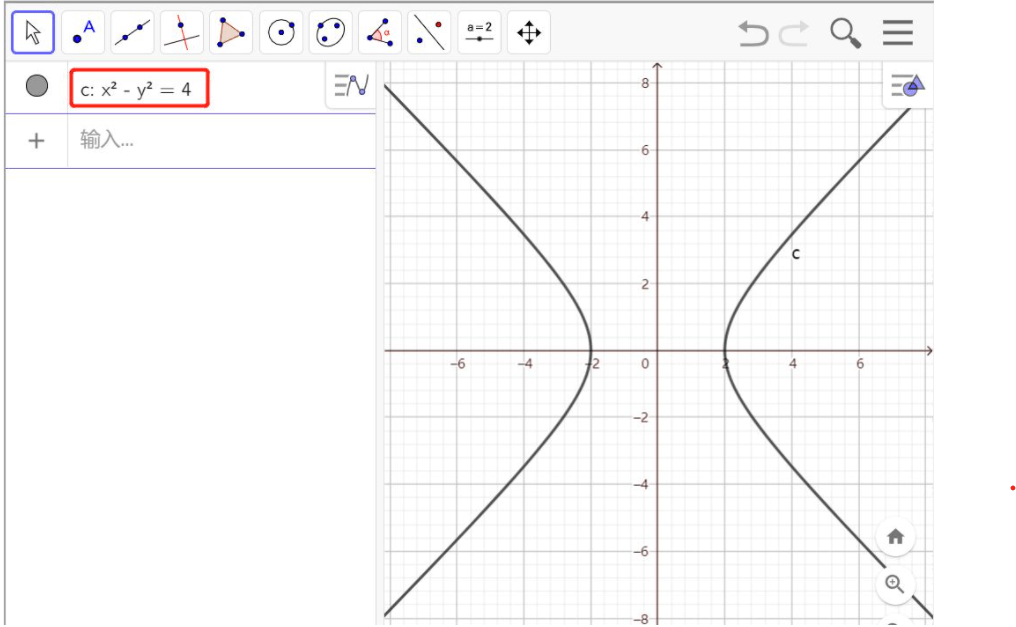
Meaning any dot on these two curve has same distance – 2 – to the origin O.

Now let’s apply this to “twin paradox”, reducing it to a simple problem. Before that, we need to grasp the concept of “世界线的线长等于固有时“.