Differentiation Geometry is a must path to truly understand Einstein’s General Relativity hence any one living in this era needs to learn.

Faculty of Khan is a good tutor in guiding through basics of DG even he describes himself as just a university student.

First is to define “curve” using precise math language:

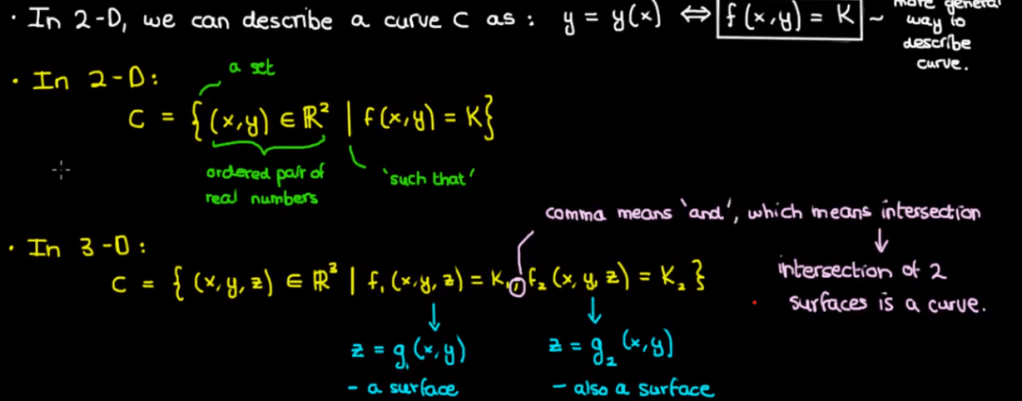
Then what if we need to describe curve in multiple-dimensional space, it leads to the important concept of “parameterization”.

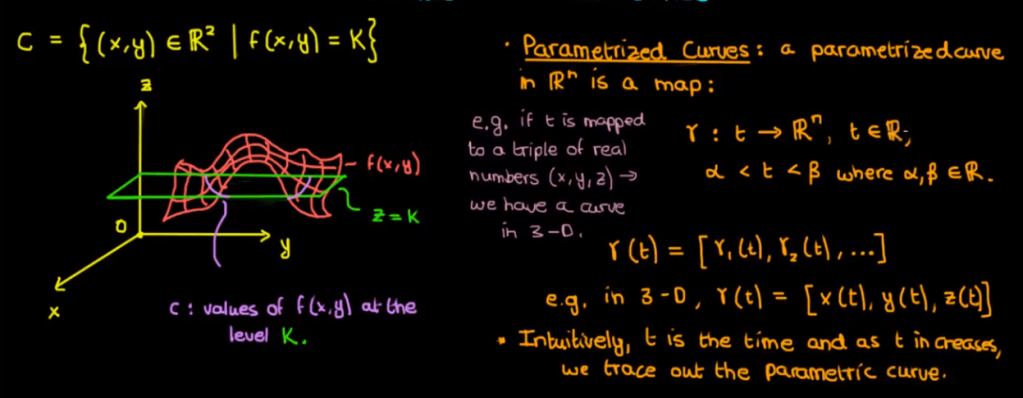
Single out one dimension f(t), on the open interval (alpha, beta), the derivative d^n(f)/d^n(t) exists for all n>=1 and all t in between alpha and beta, then this function is smooth, cascading to all dimensions, we have the following:

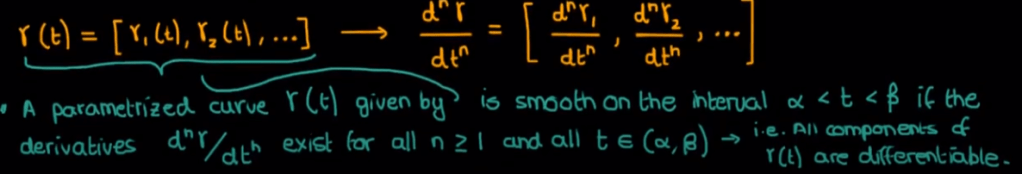
Let’s try to solve a small problem of finding the parameterized curve corresponding to y2 – x2 = 1?

A derivative problem is to find the tangent vector dr/dt

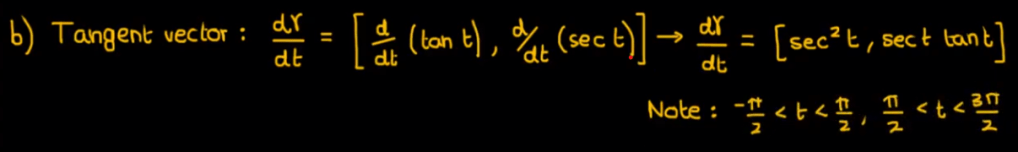
Another important concept is “reparametrization”:

To understand it more concretely, let’s see the simple equation

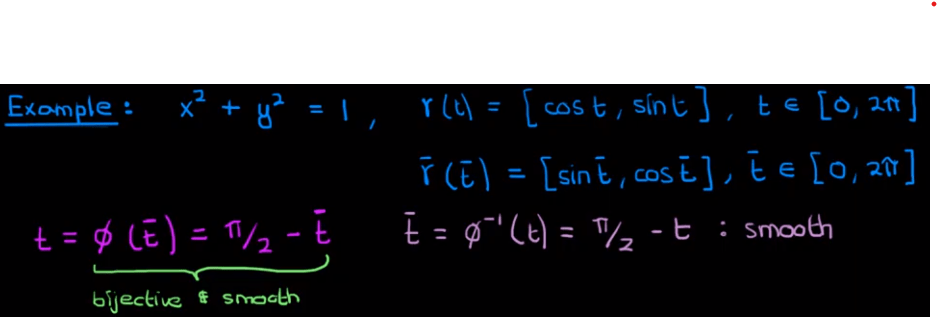
Suppose r is a parametrized curve, then we call r(t) is a regular point if r(t) derivative != 0, and singular point if is 0, we call r a regular curve if all r(t) derivatives are != 0 at all points of the curve.