Following on “Mathematics for Physics” series provided by professor Alex Flournoy at Colorado School of Mines.

First a broad outline of this course:

The outline on his website is

Introduction and Vector Space
Linear Independence, base, isomorphisms and linear operators
linear transformation/operators, their inverse, matrix realization and their properties
I can trace out the determinant, but not its inverse
Mr. Bases, you are quite similar to Mr. Eugen
Multiplicity, Diagonally and the inner stuff
In search of the orthonormal basis
determinant which is more adjoint, self-adjoint, symmetric or Hermitian
Isometrics, the Big picture and the normal picture
diagonalizing the normal
solving linear and minima
nondegenerate perturbation theory
degenerate perturbation theory
to infinity and beyond
the completeness of infinity
the Dirac Spike and Polynomial goodness
Legendre, Laguerre and Hermite walk into a bar
the purfect sturm
what the Fourier
more Fourier and his marriage to Legendre
an analytical analysis of analytical stuff
integrating the analytical stuff
expanding into unknown and all its residue
green and Dirac walk into a delta online
Green and Dirac walk into a Delta in 3D
Green’s Paint Application

A group is a system {G, .} that consists of a set of G w/ a single operation . that satisfies the following

1. . is closed, i.e. for a, b belong to G, a.b = c also belongs to G
2. . is associative, for a, b, c belong to G, a.(b.c) = (a.b).c
3. there exists an identical e belong to G, s.t. for a belongs to G, a.e = e.a = a
4. for every a belongs to G, there exists an inverse a^- belongs to G, s.t. a.a^-1 = a^-1.a = e

for example if the G is real number group |R, if the composition . is addition sign + then the identity e is 0; if the composition sign is multiplication x then the identity is 1.

Moving on the definition of FIELD:

So if you are doing multiplication/division and addition/subtraction of values in the real number Group R, you are dealing with the fields.

Finally go the definition of vector: A vector space over a field F is the set of vectors V satisfies:

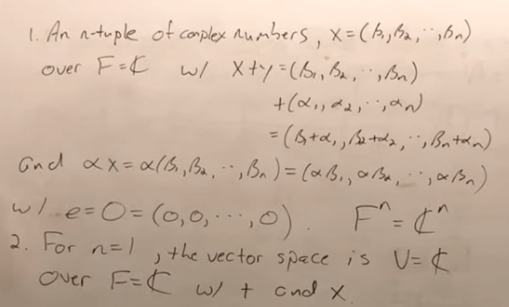
Can I take a n-tuple real numbers over F = complex number field, it would not work as it will be turned into complex in X+Y…

Another example of applying definitio of vector space, “The set of polynomials to order n that are functions of a real variable t with/real and complex coefficients, these are V = Pn over F =IR/C

Note to prove it’s a vector, he completely proved all properties defined as true. In particular, X’s inverse X^-1 in a composition sign = + case here, it is the element that complete it to be itself, so it’s -X.(X-X=0 which is e; an dit’s closed, meaning spit out the element belongs to the same field).

Conducting further investigation on “vector space” through wikipedia: “Elements of V are commonly called vectors. Elements of F are commonly called scalars. Common symbols for denoting vector spaces include U, V, and W“. When the scalar field F is the real numbers R, the vector space is called a real vector space. When the scalar field is the complex numbers C, the vector space is called a complex vector space. These two cases are the ones used most often in engineering. The general definition of a vector space allows scalars to be elements of any fixed field F. The notion is then known as an F–vector space or a vector space over F.

The simplest example of a vector space is the trivial one: {0}, which contains only the zero vector. A basis for this space is the empty set, so that {0} is the 0-dimensional vector space over F. Every vector space over F contains a subspace isomorphic to this one.

The zero vector space is different than the null space of a linear operator L, which is the kernel of L. Field itself is also a simple example of vector space. F is a 1-dimensional vector space over itself. F has just two subspaces: {0} and itself.