Continue on the multivariable calculus basics before forging into perturbation theory.

Scalar field line integral physically means the area, it is independent on the direction.

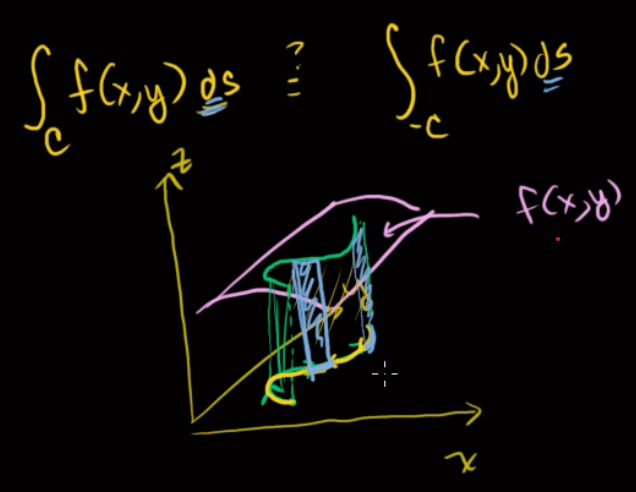
While Vector field line integrals dependent on path direction.

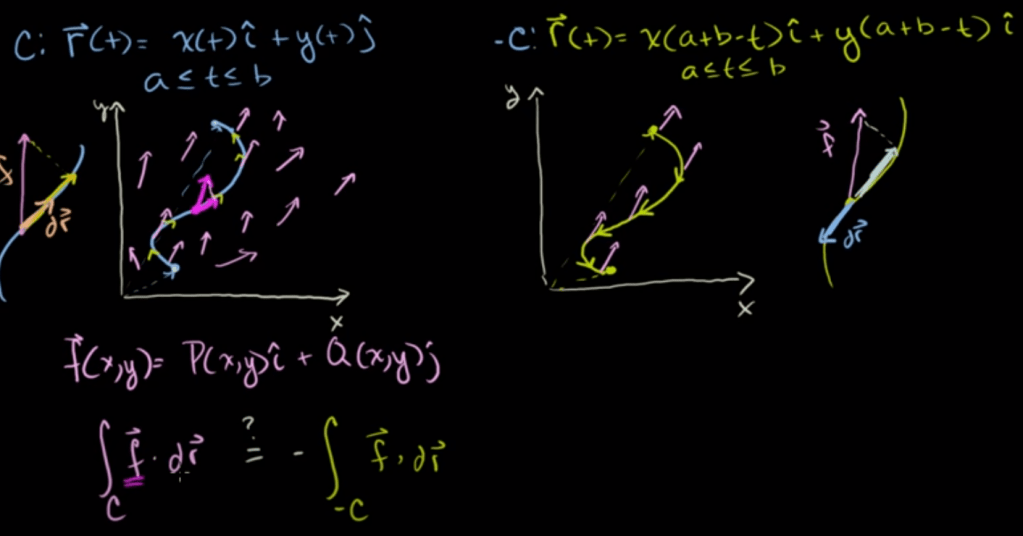
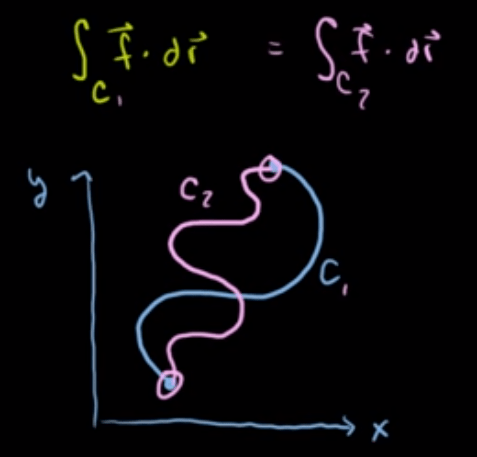
It’s worth high level of noting that in vector field, even direction of the path matters, the individual path form doesn’t as long as the starting and destination points are fixed.

This is conditioned on that f vector is a gradient of a scaler function. We call it conservative if so.

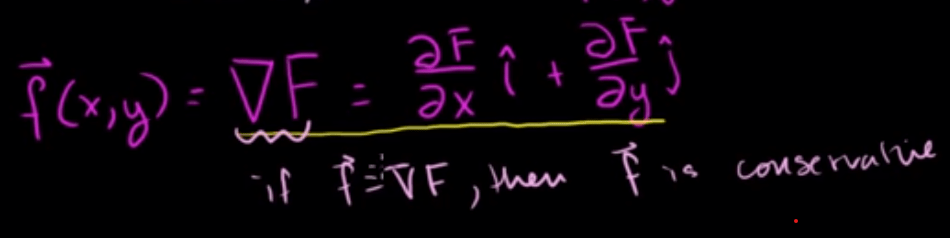
For the path, it’s described as below

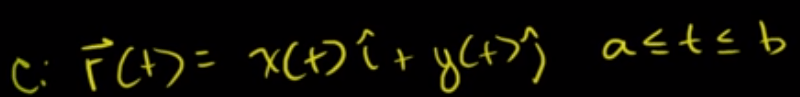
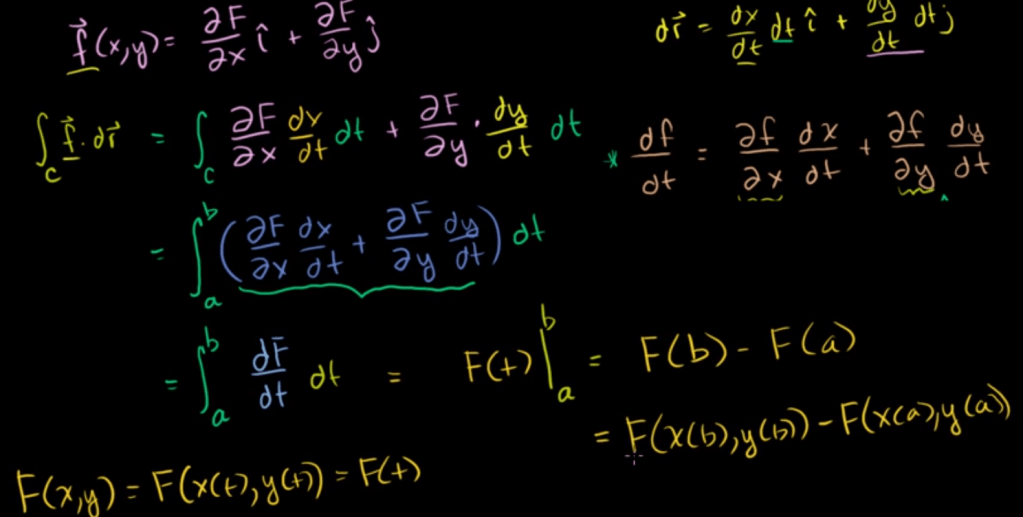
This is reminiscent of the two-dimensional area calculation problem, you can approximate by adding tiny rectangles with infinitesimal width, but the accurate approach is to find it’s integral and take F(b) – F(a). One caveat is that in that simple case, the notion of “conservative” does not exist, while in line integral in vector field does. Expanding on physics, lots of fields such as energy, momentum are conservative.

Easily, one can infer that Closed curve line integrals of conservative vector fields is zero.

Next exciting thing to learn parametrizing a surface with two parameters to draw torus.

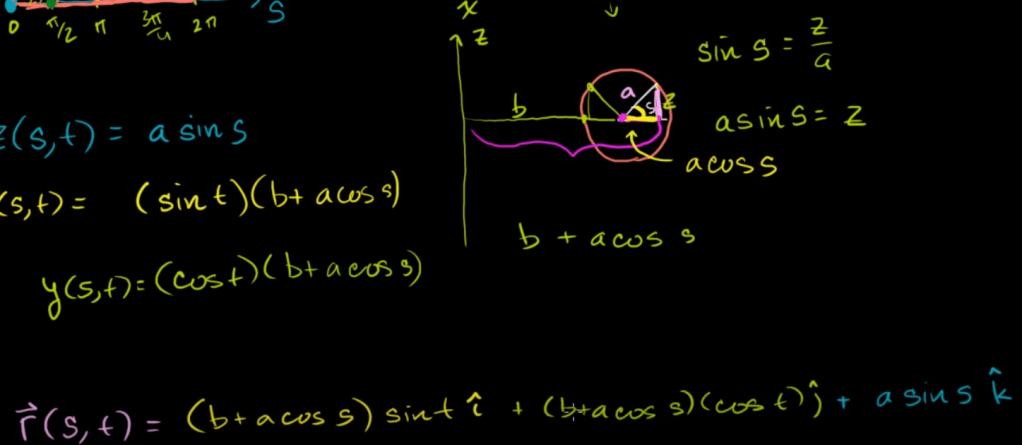
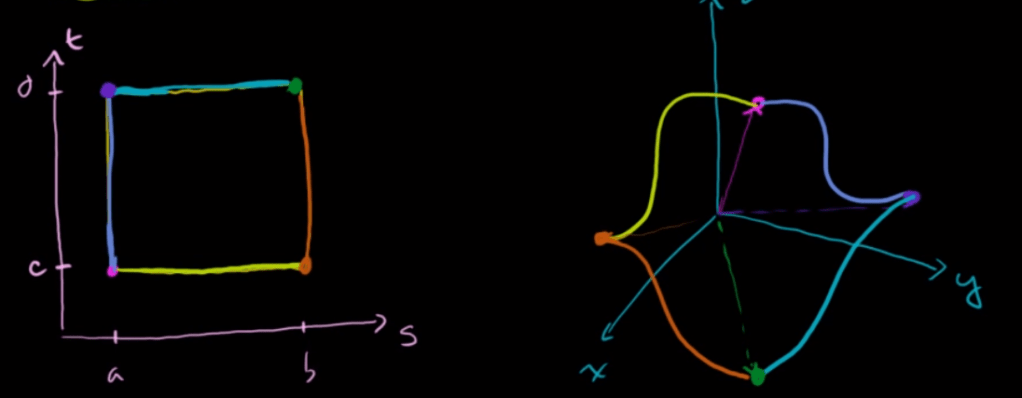
The surface of mapped area can be integred as

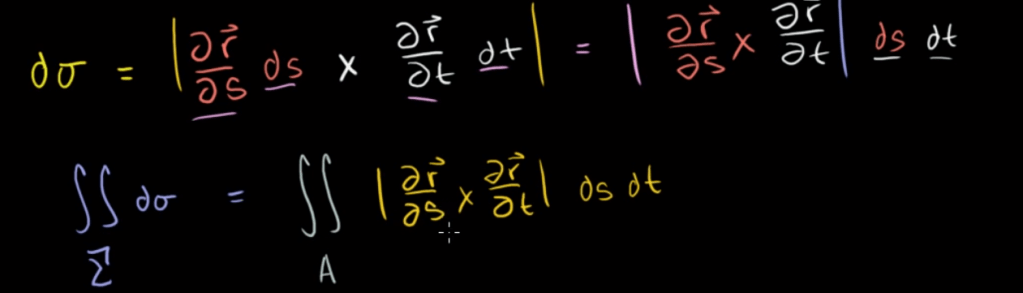
If we can visualize a surface by two parameters, it’s just mechanical calculation. The difficult part is to parameterize.

Another example is

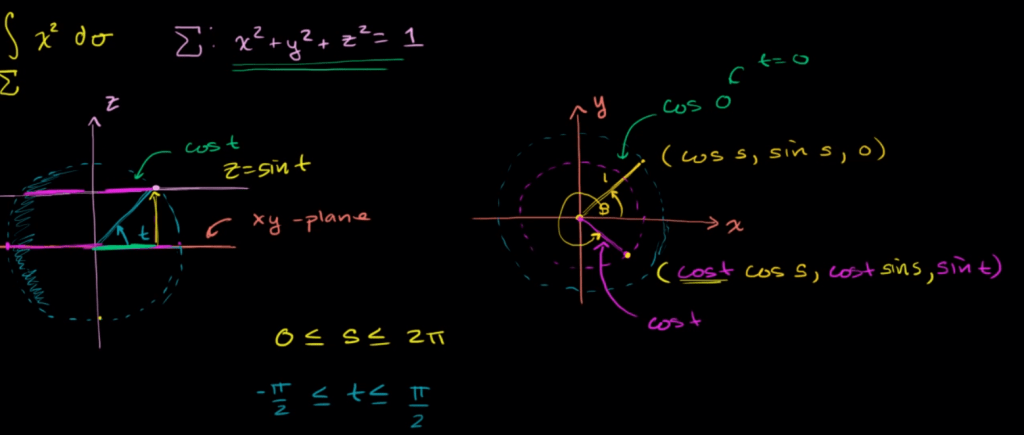
Even the calculation is mechanical, it’s important to be proficient in applying common substitute rules in doing integrals such as below

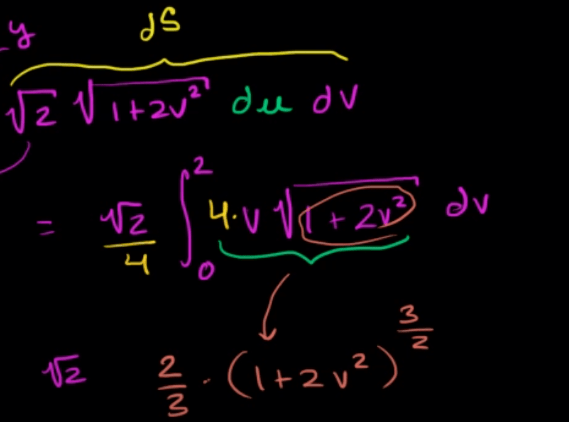
Concepts that are important:

First, flux, it’s expressed as in the following double integral denoting the flux through a 2-D surface.

the unit normal vector is

with this bridge we arrive

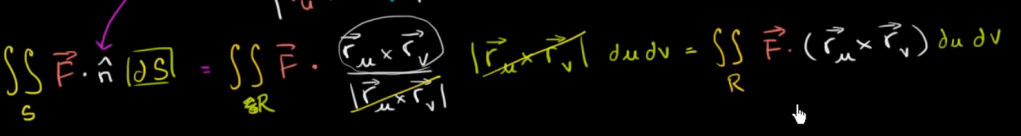
same as

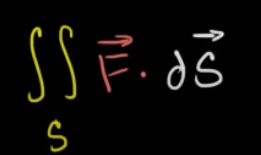
Next, Green’s theorem, basically says that path integral on a vector field can be calculated as the subtracting Q (j part) derivative on x( or i direction) and P(i part) derivative on y(or j direction) integrated on the region.

It’s basically a 2D divergence:

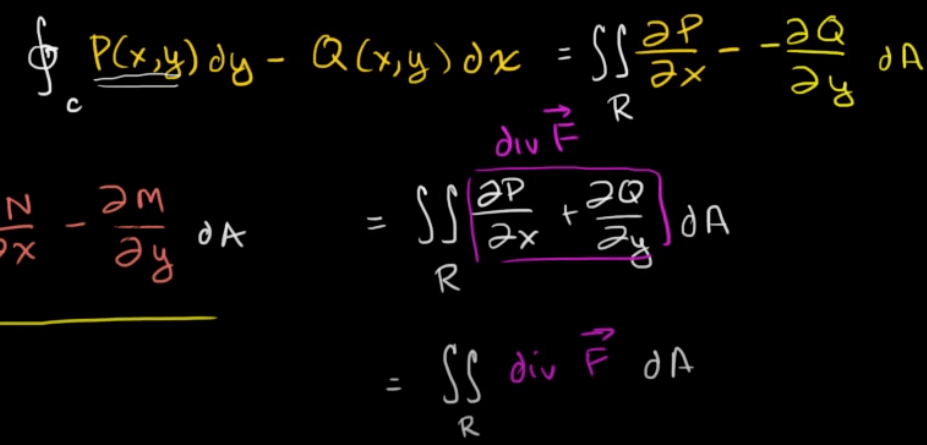
Next Stoke’s Theorem, it’s essentially just more generic form of Green’s theorem – The line integral of a vector field over a loop is equal to the flux of its curl through the enclosed surface.