Tensor is essential in understanding Einstein’s General Relativity and nowadays AI, however, it’s not an easy topic to grasp hence I dive deep to find eigenchris’ series the most helpful.

So what is Tensor? The first intuitive definition is it’s like multi-matrix with different ranks. Rank 0 tensor is composed of one scalar, rank 1 means there is one dimension, so on and so forth.

Tensor is an object that is invariant under a change of coordinates, and has components that change in a special, predictable way under a change of coordinates. Or, it can be defined as a collection of vectors and covectors combined together using the tensor product. An extra definition flavor is given as Tensor is partial derivatives and gradients that transform with the Jacobian Matrix.

To understand tensor’s invariant property, let’s look at two coordinate system converting between each other:

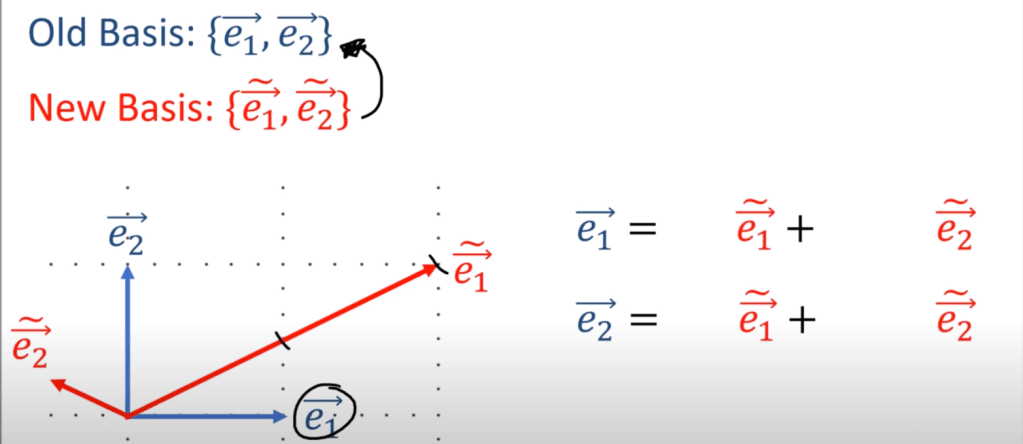
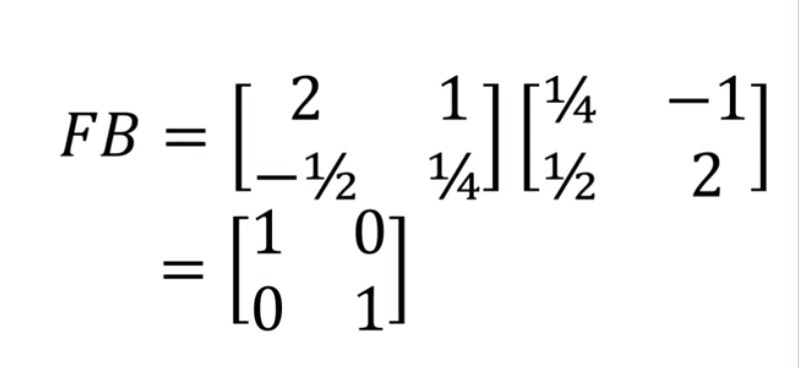
Put it in a more generic form it looks like this:

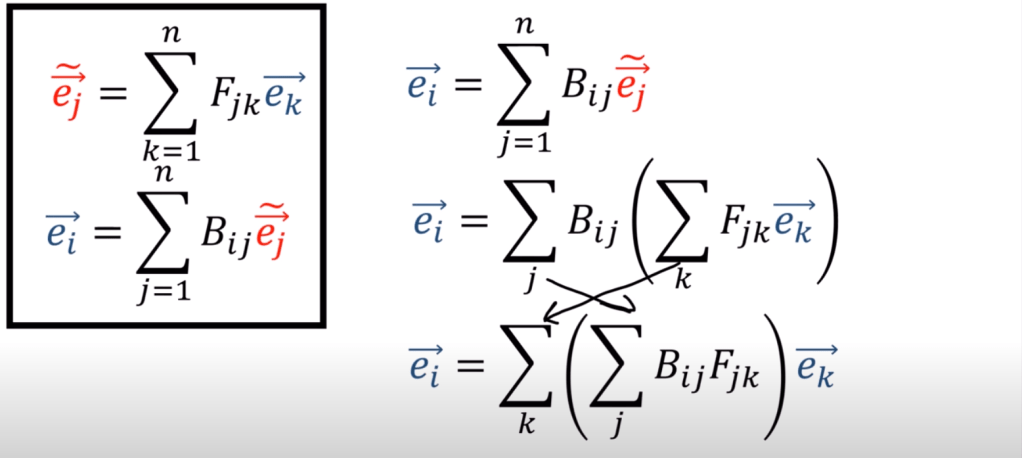
Since ei vector and ek vector are identical so we need to make the part in front of ek vector an identical matrix and satsify the below 1 or 0 conditions, leading to the famous Kronecker Delta.

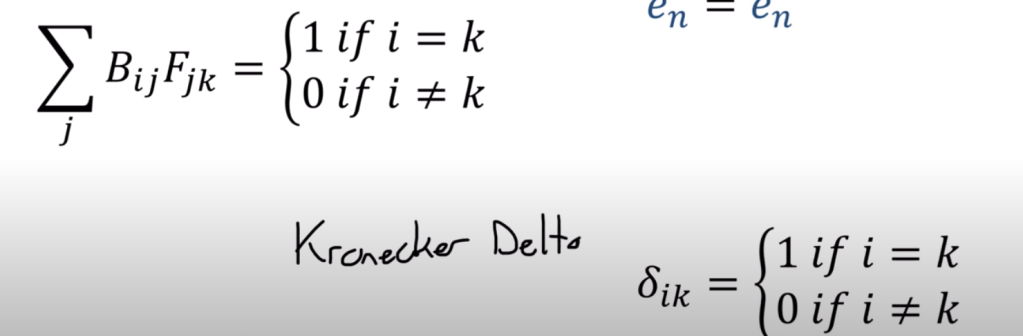
Then what is vector?

Since the basis can be different in different coordinate system, the vectors defined by these basis however is invariant, that means the component scalar forming vectors have to be changed, and the way they change obeys a reverse rule: the old components times backward matrix to get the new components and the new components times forward matrix to get the old components.

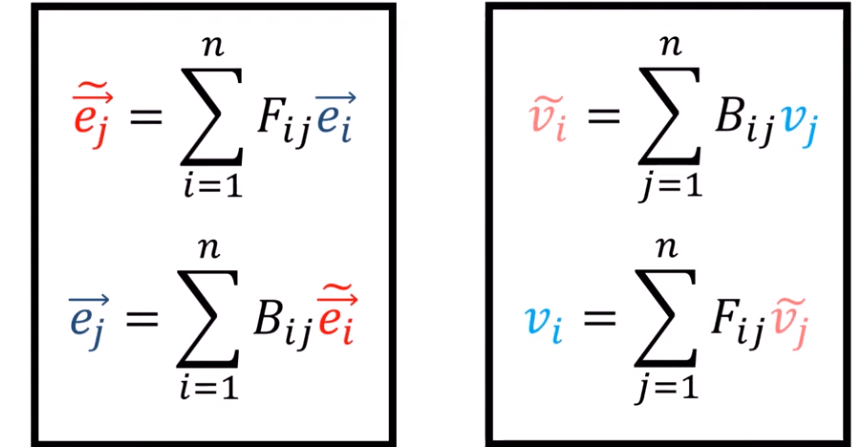
To conclude again, the basis is Variant, while the component is Contravariant. To make it easy to tell, the notation is modified to move subscript i to upper part as:

Next what is covector?

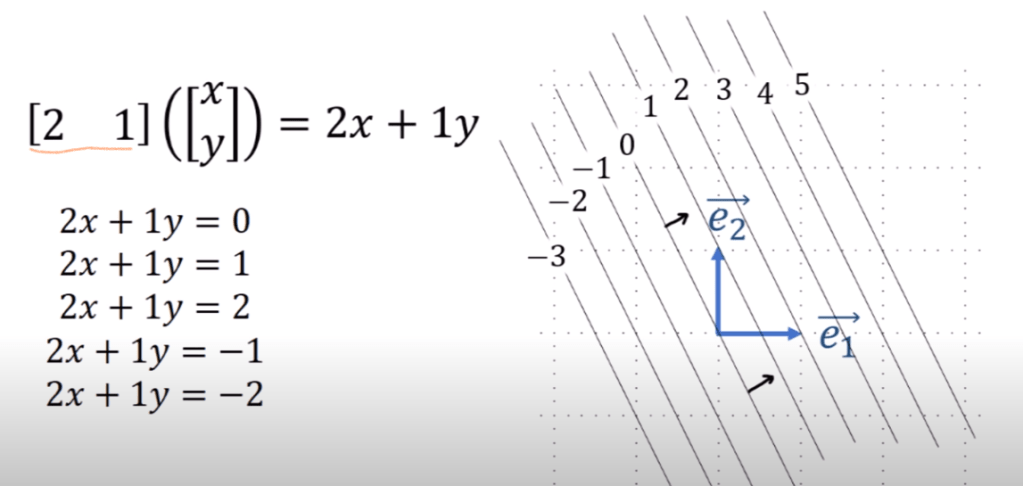
We can think of it as row vector, and row vector basically can think of as a function on column vectors. To visualize covector, we borrow the geographic map idea and draw a stack of lines with perpendicular direction.

If we need to add up two covectors, the visual would be

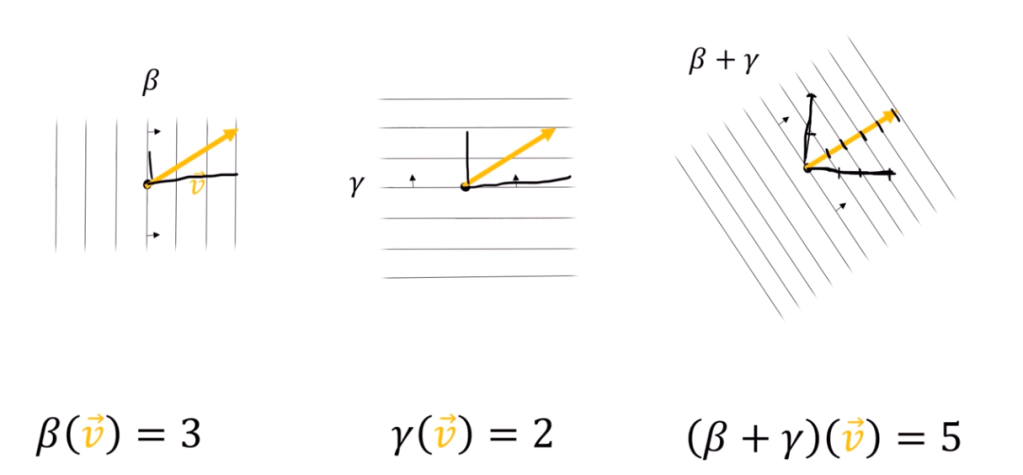
Covectors V* do not live in the same vector Space V, we give it another name “dual vector space”. In order to parse covector an invariant, into components, we still use basis like ei and ej vectors but with additional math manipulation here:

This make the basis of covector be able to project(function) any vector onto its respective basis component in vector space

We also want to check if the dual space V* obey the same converting direction as Vector space V?

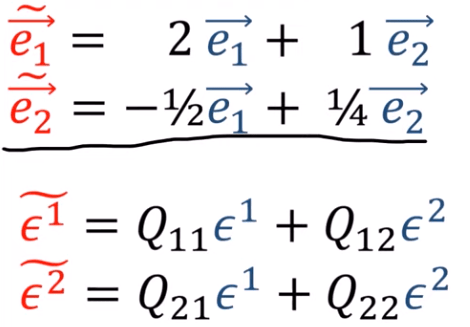
It turns out they are opposite to basis in V,

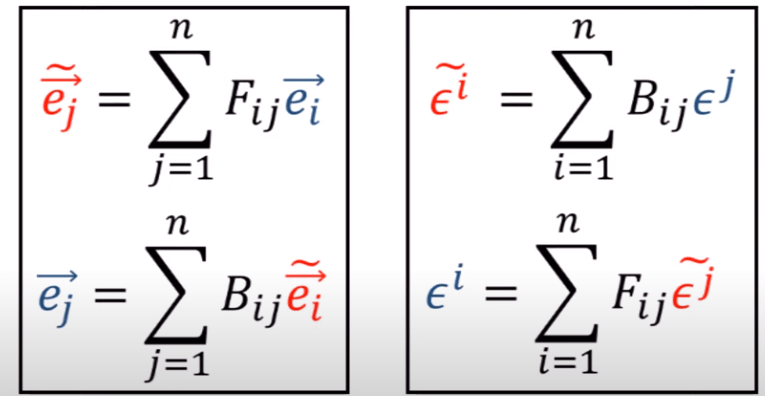
Lastly, what is Linear Map? Just as we think of column vector as Vectors, row vectors as Covectors, Matrices are Linear Maps.

As to how linear maps(matrices) works,

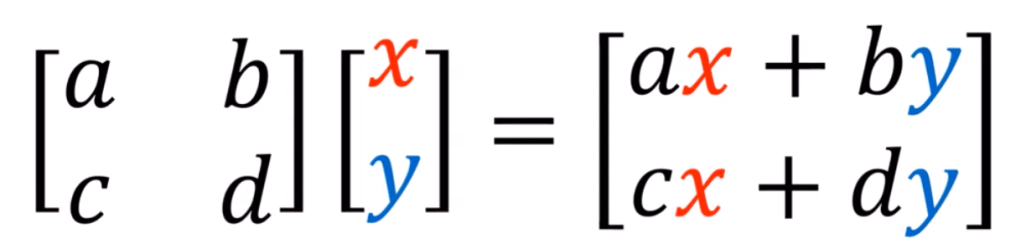
note if column vector time row vector it is

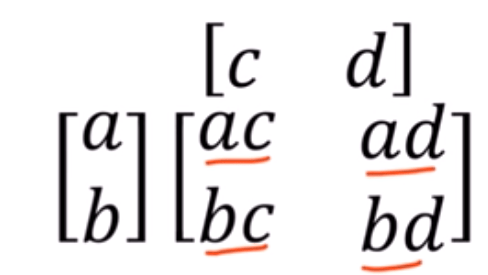
the 3B1B already shed light on the thought process geometrically: essentially, it keeps gridlines parallel, gridlines evenly spaced and the origin stationary.

To figure out the transform rules for matrices/linear maps, it could quick turn very hairy like below:

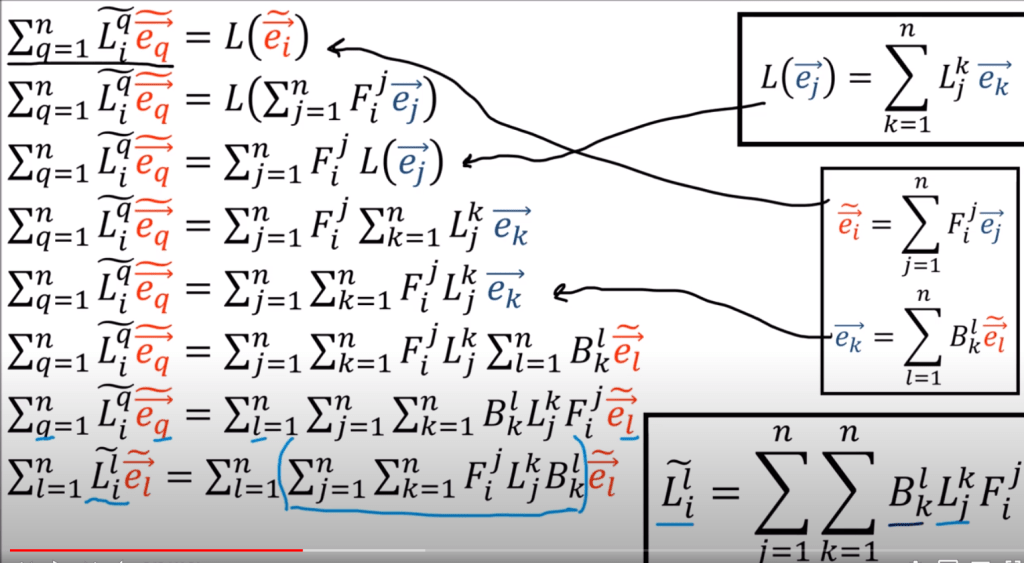
The key take away is the formula in right bottom, one backward one forward staying left and right side around the linear map L j,k. It’s actually intuitively straightforward as is indicated below

note the above the deductions are quite ugly and too much to write, introducing Einstein’s notation to remove summation sing, they can be reduced to

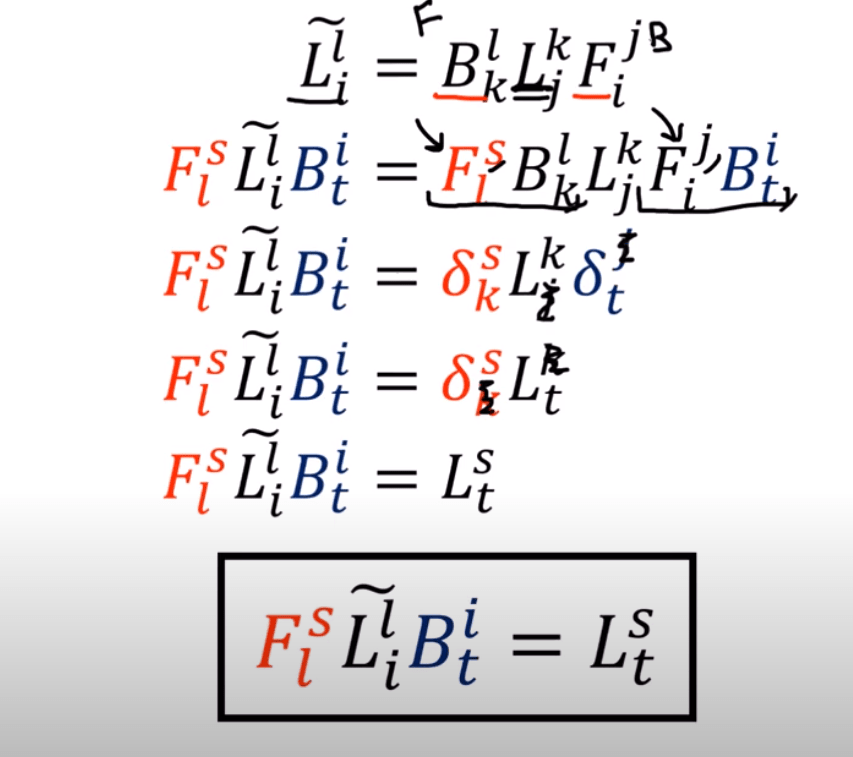
So sum up, the vector transformation requires same direction Backward or Forward transforming, we call (0, 1) tensor, Covectors we call (1, 0) tensor, while linear map, the third type of tensor is called (1, 1) tensor.

Finally what is Metric Tensor? This is applicable in a universal need – to calculate the length of a vector, orthonormal based Euclid square is not valid anymore. A generic form should be

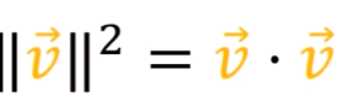
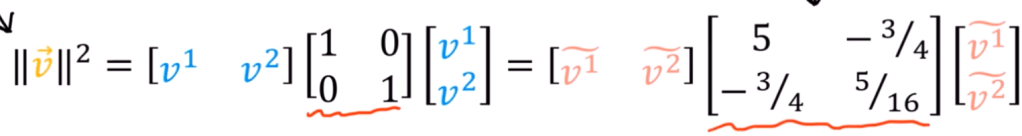
This add to the another type of tensor (0, 2) tensor since the convertion between two coordinate system is either two Forward or two Backward.

Metric Tensor is a function g: takes in two Vectors and spit out an Real number.

An more abstract but accurate definition of tensor is that it’s a collection of vectors and covectors combined together using the tensor product.

For example, linear maps is just linear combination of vector and covector pairs:

bilinear forms (metric tensor) is just linear combination of covector-covector pairs:

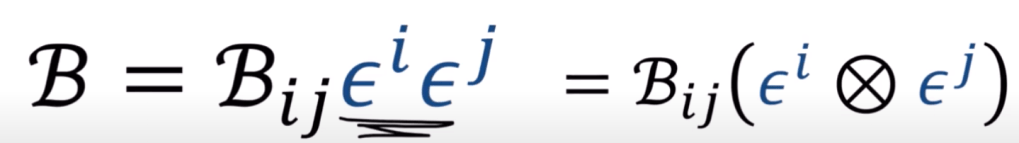
Adding on the materials from Dr. Grind(MathTheBeautiful), his interpretation is from another angle making lot of sense.

At the core, his idea is to abandon the cartesian or polar whatsoever coordinate system but to define a vector in a more liberal and powerful way. Arc length is an essential way in implementing it.

So, a vector R is invariant, to define R, one can use differential R to any frame dimension (gradient, covariant basis) to get the coordinate. for example, any random curve s at the direction of unit n, can be broken down to two unit axies n1, n2.

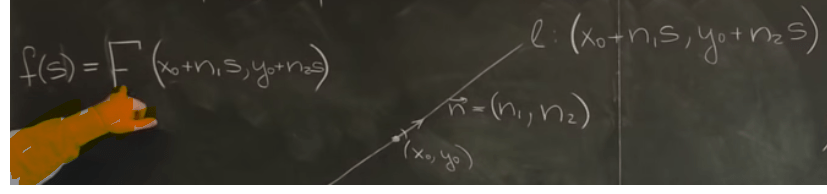
From this profound idea, the Torricelli’s and Heron’s Problems are can be described in calculus: the sum of the gradient of two/three segments be minimized. … concluding the three unit vector ?(more to investigate)

Not using F and B to convert between two coordinate systems, his approach is more intuitive, starting from

Taking derivative orderly dr/dr, dr/dtheta, dtheta/dr, dtheta/dtheta, dx/dx, dx/dy, dy/dx, dy/dy for above (note the first r is the function, while the r on the right side of the equation is an independent value. Thus, he introduces Jacobian matrix. Functionally, this jacobian is same as EigenChris’s jacobian in the sense that it converts between old and new coordinate systems.

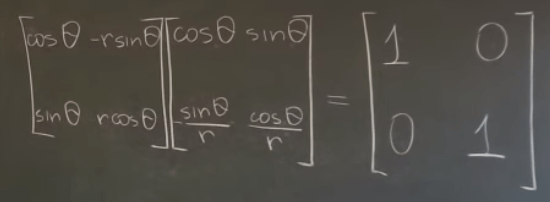
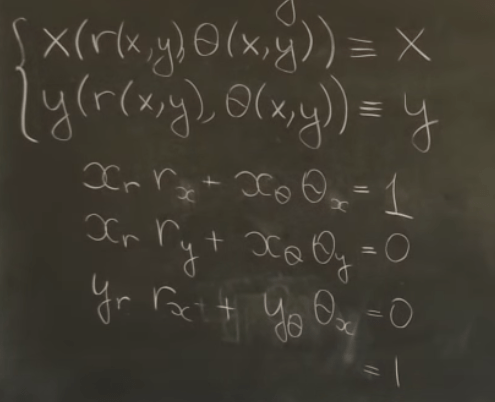
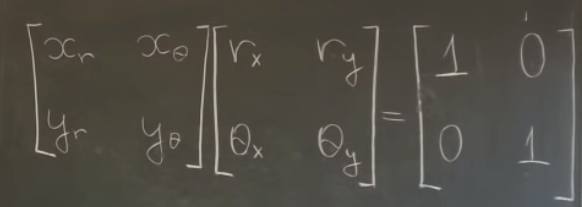
Einstein Notation (Tensor Notation) is quite baffling. The layout is much more sensible in his approach even it still requires devoting time to practice and familiarize.

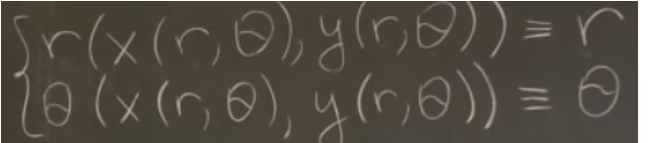
The Kronecker product is more sensible here too

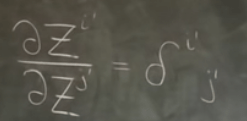
So the former form

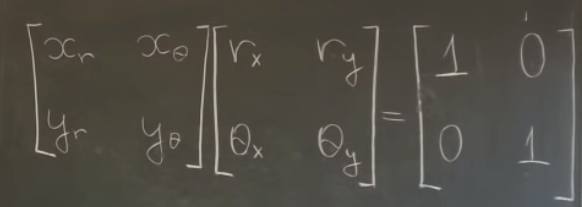
is written as below

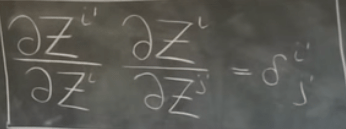
Finally everything started to sync, to define Contravariant and covarient tensors and mixed tensors.
Suppose that V is a matrix field composed of n x n scalar fields (functions) defined over a region U in Rn. Assume that in the (xi) coordinate system, the components of V are Vij. assume also that after a coordinate transformation

There is the concept of general tensor too:

On Dec 2021, adding further learning from Dr. Nathan Kutz, instead of vectorizing/flattening, we try to keep the higher dimension data, which is Tensor, to apply similarly SVD method, and this is called Tensor Decomposition. Different normal matrix decomposition, which only have one unique way, Tensor decomposition could have multiple ways.

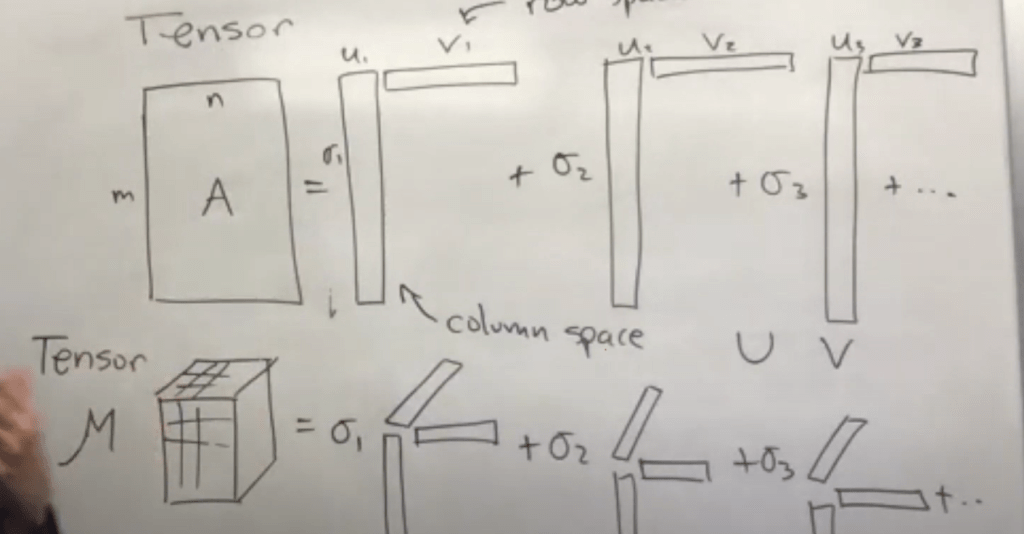
Tensors are fundamental in physics because they allow physical laws to be expressed in a form that is independent of the choice of coordinate system. Here are some key examples across different fields: