So the derivatives are basically vectors, we can apply Tensor concepts just learned to derivatives problems, which is quite universal in physics world.

Any derivative (tangent line along a path) can be expressed by various coordinate system using coefficient(entries to matrix) and coordinate basis. Jacobian matrix and inverse Jacobian matrix accomplish conversion between them with the components partial derivatives to each other.

To study a simple circular path as below,

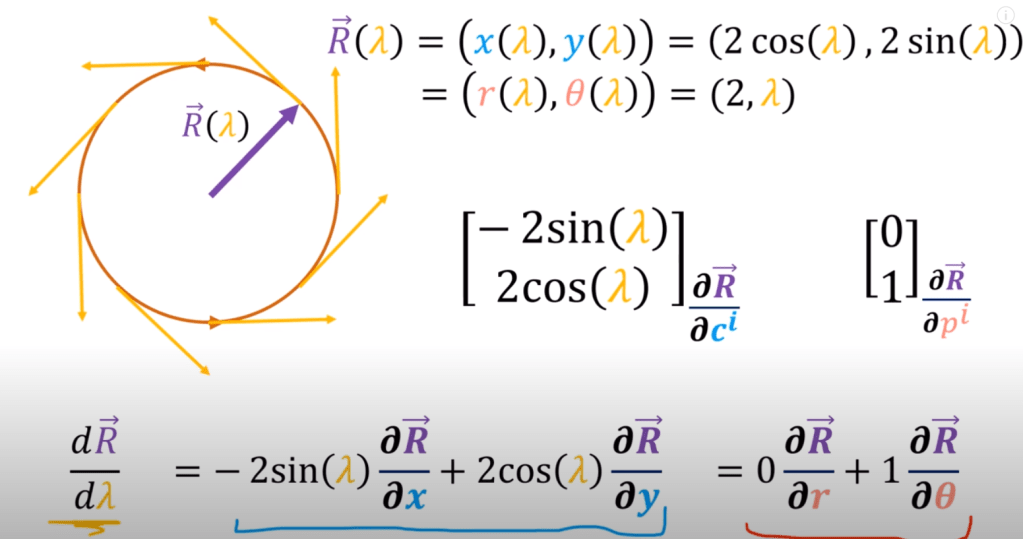
Or, to write it more compactly using Einstein notation:

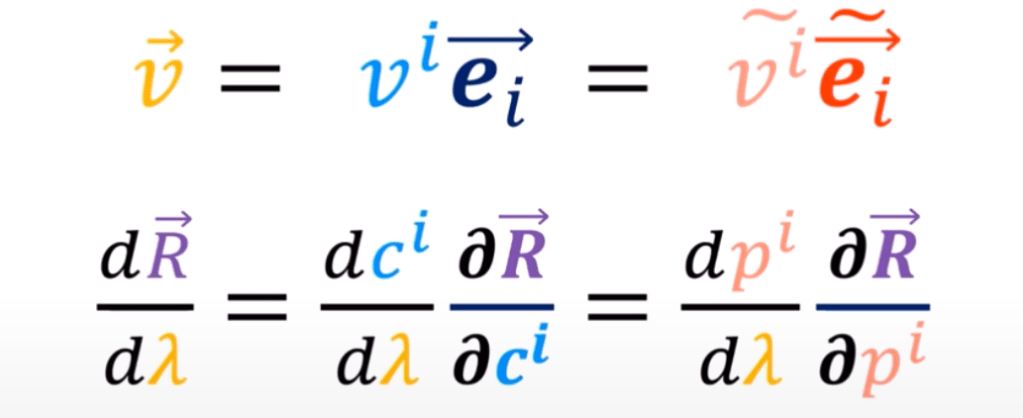
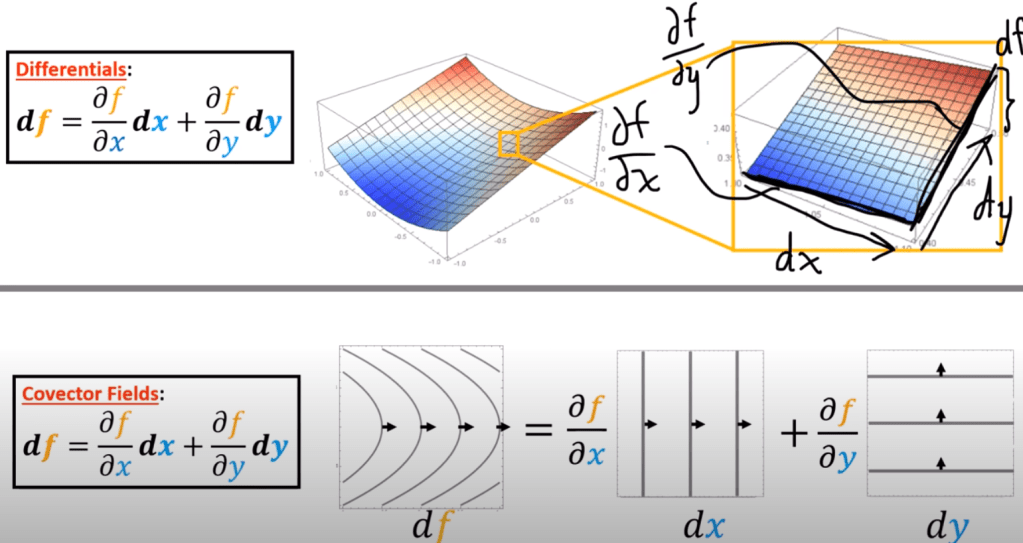
The next concept is that Differentials are basically covectors. It’s abstract at first glance, but the following visual help the understanding more straightforward. d, turns a scaler field represented by function f, could be temperature, into covector field df. Scalar field is also called 0 form, so df, the Covector field is 1-form.

If df is a covector, according to the definition of covector, it’s a row vector that exert on a vector form, so what turns out to be df(v vector)? The geometrical meaning of df(v) is the directional derivative of f in direction v vector.

As df is a covevtor, then we can also parse it to learn what is the component of df:

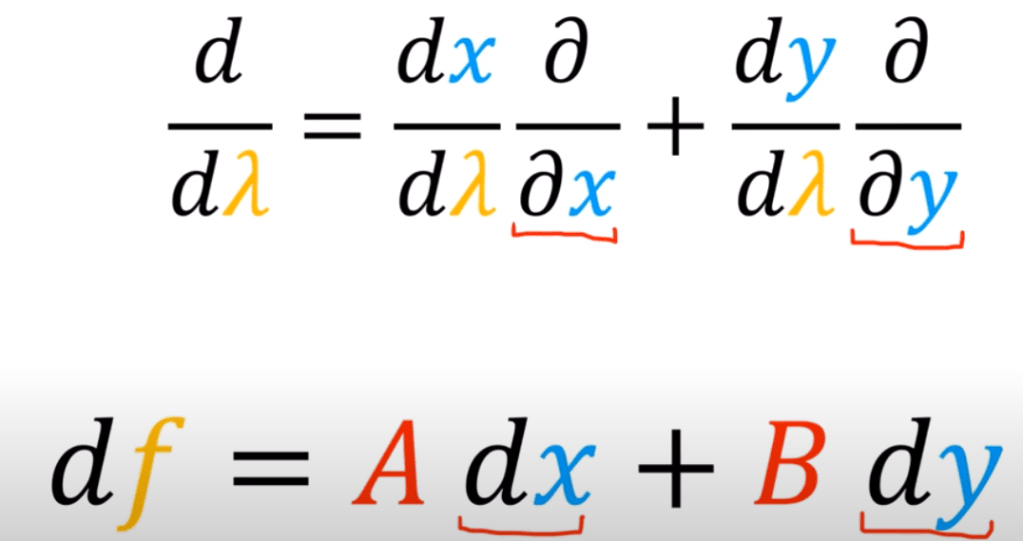
A and B can be proved to be partial derivative f to x and y respectively.

To understand it in a visual way, let’s see the below example:

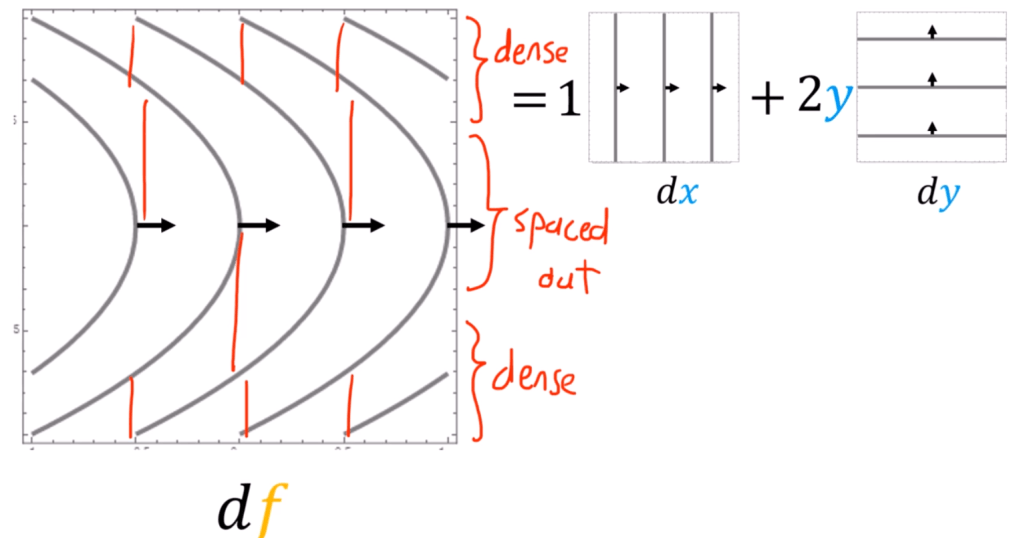
Further we try to use these math concepts in solving physics problem such as Work.

The force rendered on earth (in a gravitational field) can be converted into mass times “gravitational potential”

The gravitational is a gradient as shown in right upper corner, however, it’s much more intuitive to process -d fai, as shown in right bottom area, a covector in V* space, showing the stacked lines.

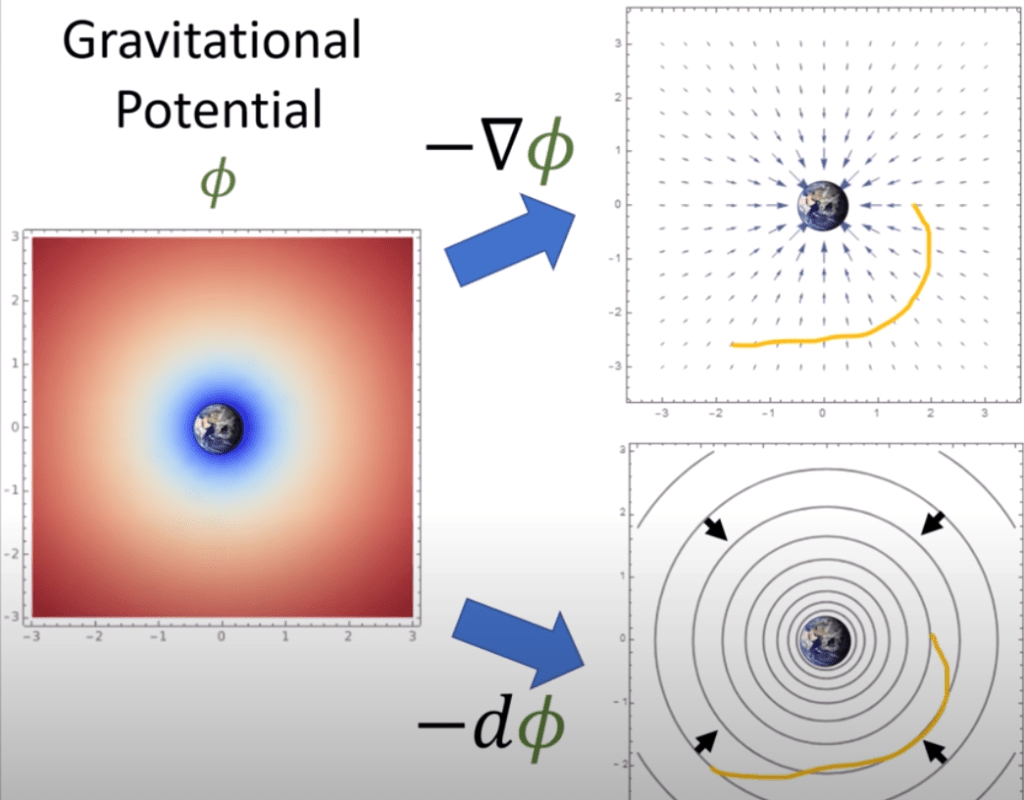
This makes integral straightforward because every integral basically involves a path and a differential form(covector field); the result of the integral is just the number of covector stacks pierced by the path(in the covector aligned direction)..

Next, introducing concrete example to show the power of “thinking of differential form as covector field”: below two integrals can be drawn in stacked lines and we just need to count the pierced units by the path, noting the path can now live standalone rather than in a Cartesian or polar frame.