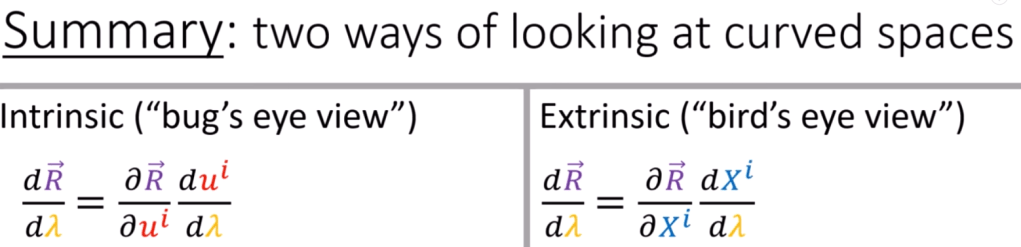How to define and calculate length of a vector in any space, knowing space can vary in different basis frame? It’s the dot product of the vector itself, then taking root square. But why? It’s equivalent to multiply each component of the two vectors(itself here).

Turns out it can be more algebraically written as below for an custom vector in two cartisian frames.

One can see the metric tensor g here is can be compactly expressed as

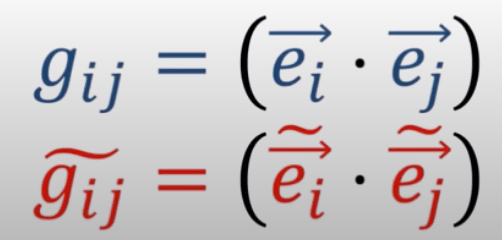
According to Dr.G, it’s worth noting it’s not written as gij, but Zij, the dot product of its(manifold, curve etc. that we are trying to measure and study) covariant basis.

Why emphasize metric tensor, it has wide application in measuring arc length not only in flat space but also curved space. That’s Why Einstein’s general relativity formula contains this element.

So, let’s measure an arc length at a 3D sphere, note what we learned in multivariable calculus about parameterization is all useful now given it’s converting between two component space and three-component space.

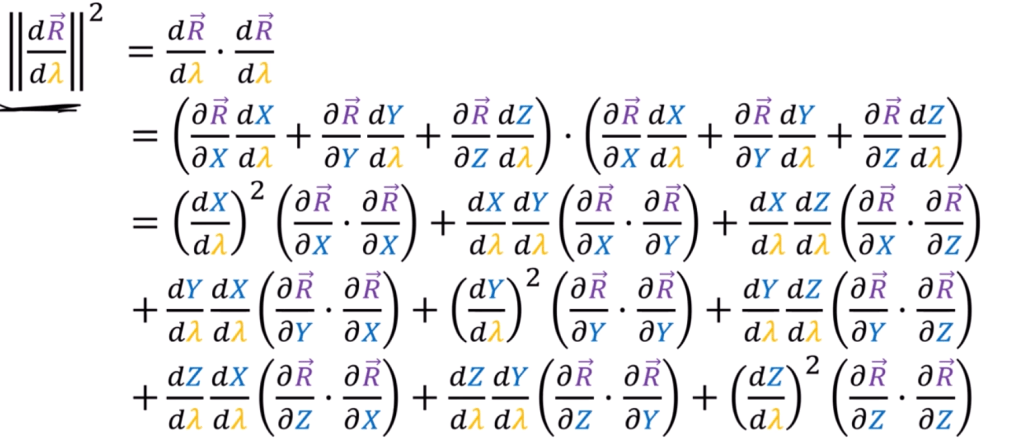
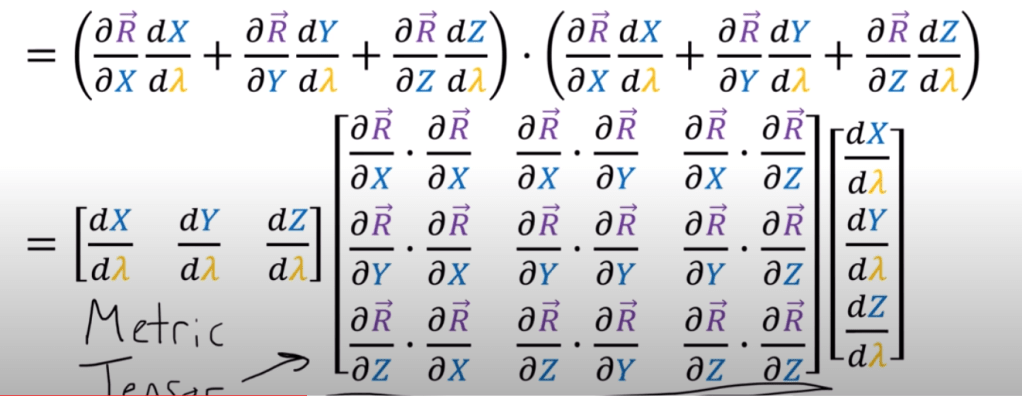
The huge block in the center is basically the metric tensor and in x, y, z space, collapsed to identical matrix. Conduct the same computation but in u, v 2D space, the metric tensor is

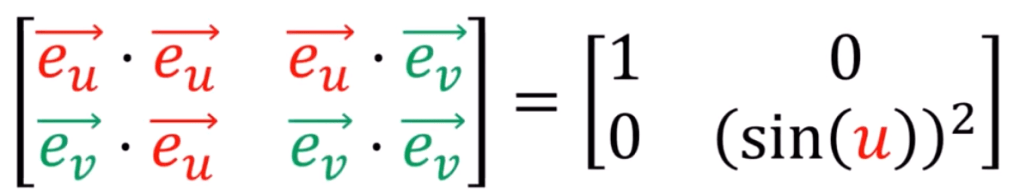
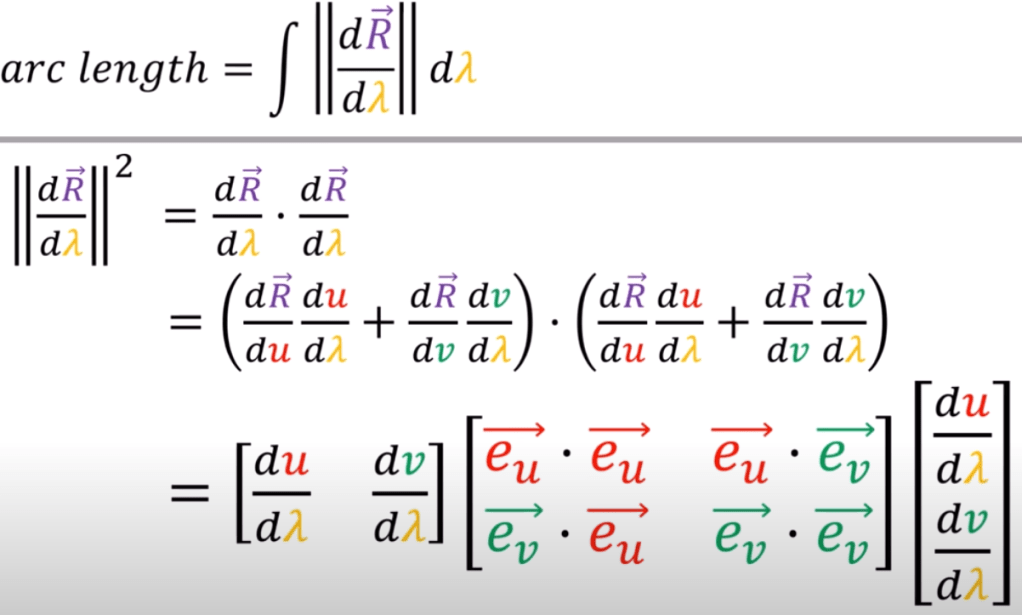
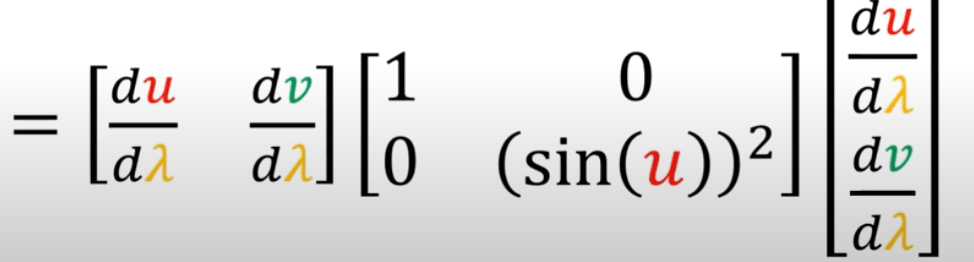
(to add later on about measuring two u v value pairs on a sphere)

Meanwhile, the notion of “metric tensor” jumps out of its meaning and importance here. Instead of a stable identical matrix for 2D space, in 3D space or multi-dimensional space, “metric tensor” matrix is essential to grasp measuring:

Since vector forms vector field, covector forms covector field, metric tensor also forms metric tensor field.