Referencing her handouts link, in conjunction to MaththeBeautiful’s (Dr.Grinfeld) series on vector calculus.

First the concept of arc length and how it is widely used a parameter to parameterize a curve.

There are multiple ways to parameterize this circle, a common practice is to use t as is shown above. Let’s assume a good parameter alpha here. Instead of using t, we directly think of the alpha as infinitesimal small arc length s, that adding another small amount h to approximating to 0, using the basic definition of derivative we can certainly reach to the understanding that at each point there is this tangent line on the curve with stable length (unit length T(s)) – derivative of the vector forming the curve. Since it’s parameter is arc length not time, we naturally conclude the derivative is unit speed (I don’t think using speed is proper here since t time is swapped by arc length) at that point.

This explanation from Dr.G is great, also I reference eigenchris’ as

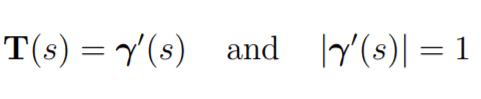
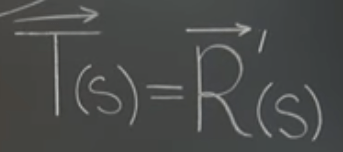
According to what that prof. talks on this episode -Derivative of a Constant-Length Vector=, it makes a lot of sense. Then according to the linear algebra, the length which is dot product of itself is the square of length is constant, constant’s derivative is zero, we get

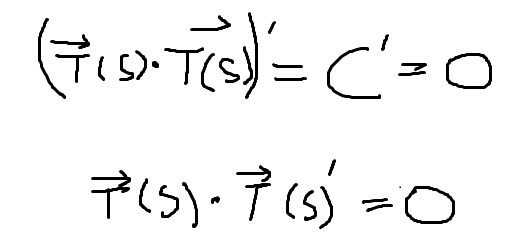
With this conclusion, we can solve geometrical problem without relying on geometric intuitive. For example, solving Heron’s Problem (to find the shortest path to go from A to the river bank then to B) using this Vector-Analytic Solution:

The key here is to mathematically define the three line vector, we use the imaginary curve’s arc length alpha as parameter, so there are R(A), R(B) and R(C) as shown below. This is a big leap in constructing vectors. Conceptually, vector is invariant but the parameterizing way can vary. (according to his own explanation: “You can think of alpha as something that lives on the curve separate from the position vector. Before the position vector is introduced, a value of alpha is associated with every point on the curve. Then you can introduce the position vector relative to various origins and they are all functions of the pre-existing alpha.

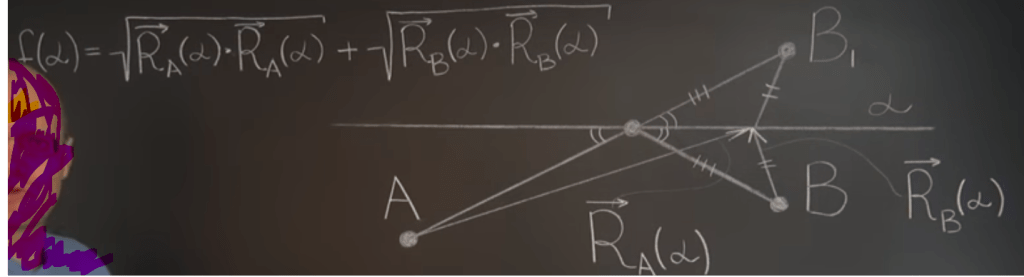
To minimize the f(x), we need to compute the derivative of f(x) and makes it equal to 0. That’s why we can refer to previous conclusion to get

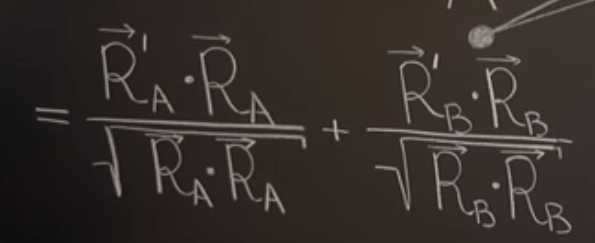
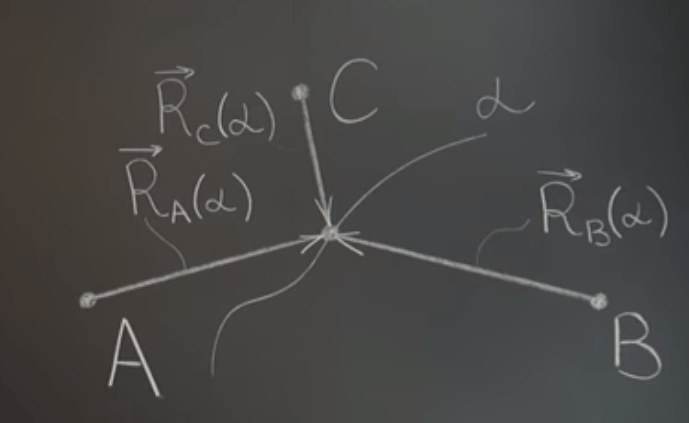
So the problem is converted to be simply trying to find the smallest sum of their length.

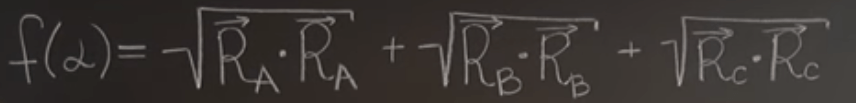
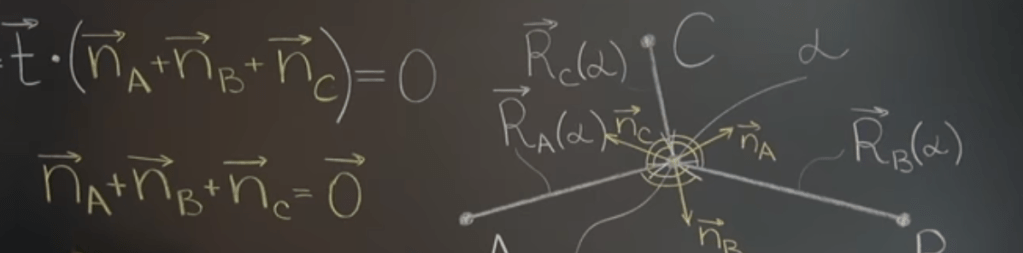
Switching gear back to curve, so The derivative of velocity vector is called acceleration vector r”(s).

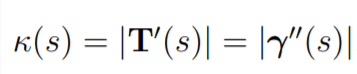
curvature k(s) is acceleration and also measures s the intensity of the force needed to keep the particle on the track of
γ, in classical Newton world, it is the Force/m.

So a straight line does not curve at all. But acceleration can be a non-zero value along a straight line.? this is an easy confusion not discerning that “the word “linear” is used in two different ways”. The following equation describes linear motion with acceleration:

For example, To find the curvature of the circle γ = (a cost, a sin t). We can obtain the parametrization of unit speed by setting

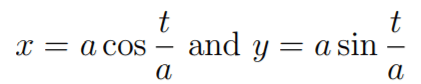
making it a unit speed curve.

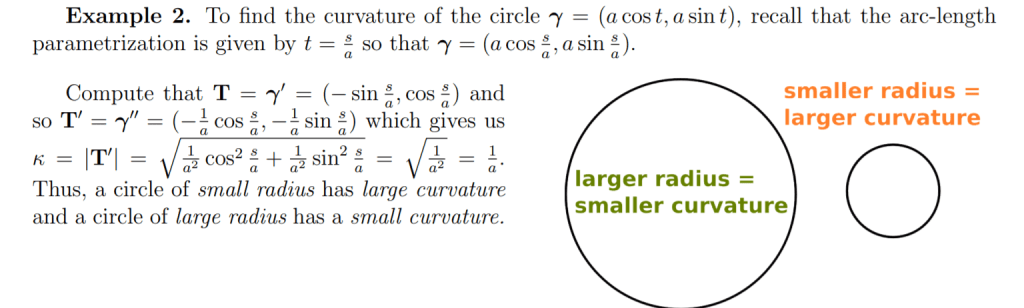
What is the curves is non-unit-speed parameterizable? A more generic formula is

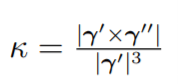
the whole process of deducing this formula is as follows

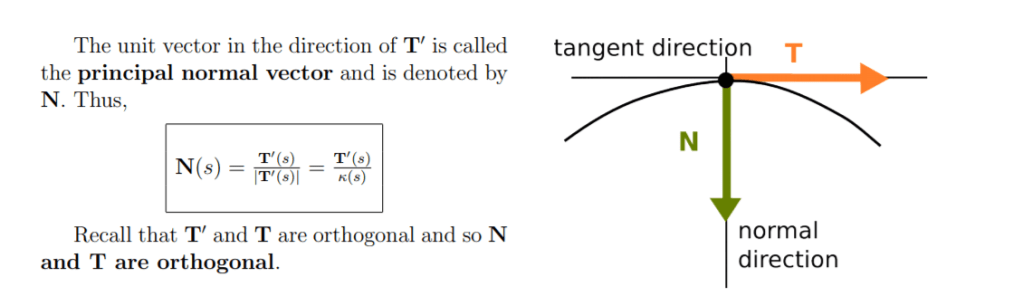
Next, several concepts are introduced, as shown below, the unit vector in the direction of T’ is called the principal normal vector, denoted by N.

The plane determined by vectors T and N is called the osculating plane. This circle is called the osculating circle.

Adding the third basis vector B, called binormal vector is perpendicular both to T and N and has unit length.

These triple T, N, B is call the moving frame.

Next important concept is Torsion. While B indicates the direction in which the curve departs from being a planar curve, the torsion τ measures the extent at which the curve departs from being a plane curve, that is, it measures how much the curve departs from the osculating plane.

Frenet-Serret System describes/states that the moving frame T, N, B is completely determined by the two functions kaba and tau (curvature and torsion). It is the fundamental theorem of differential geometry of curves