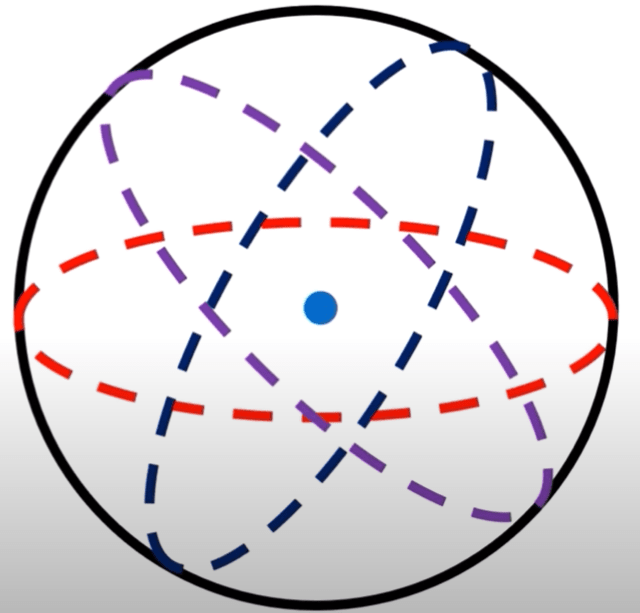
On curved space, there are more than one straight line between two points, it is called Geodesic line.
To define geodesic line, the second derivative(acceleration) is normal to the line, with no tangential acceleration if the first derivative(velocity) is constant.
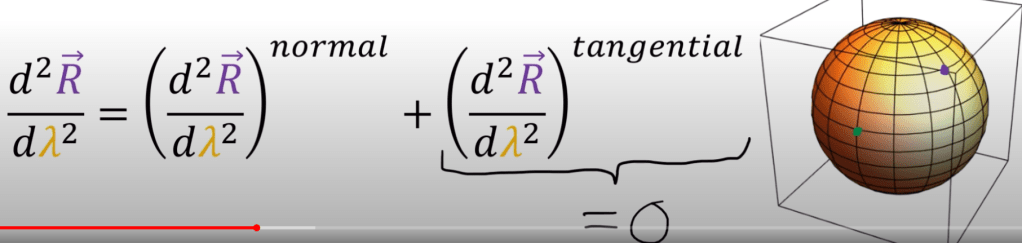

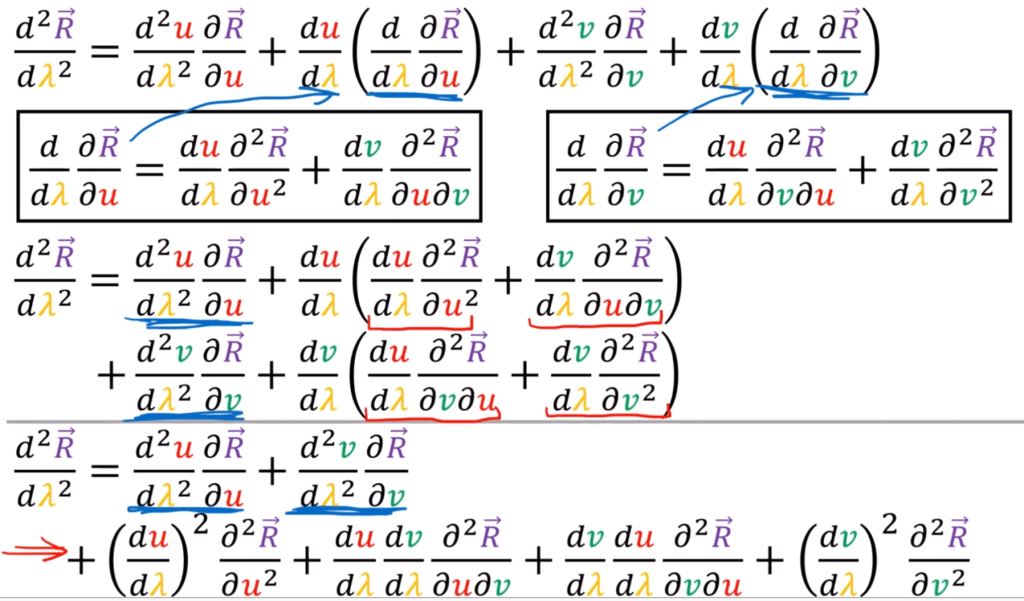
Reviewed again, the part on below is not fully clear so adding it :
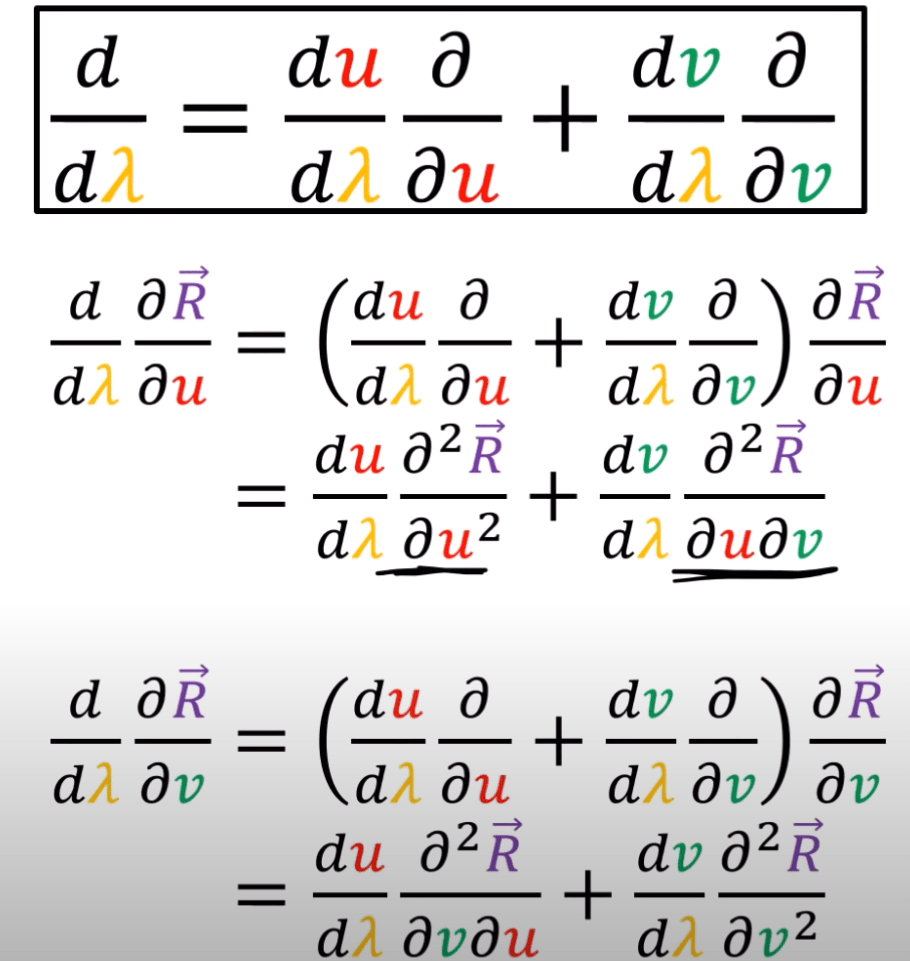
If we write u v as u1 and u2, so it can be expressed in Einstein notation
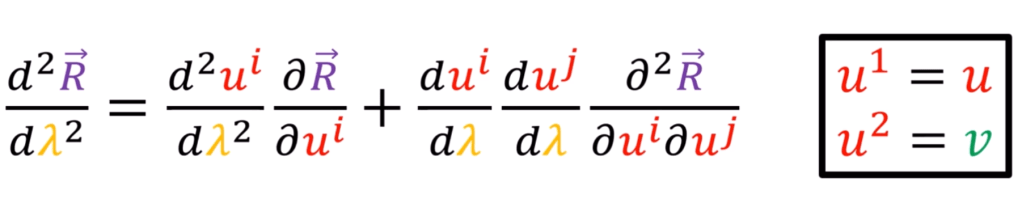
Because we don’t know what animal it is, but it exist in an 3D space, so we can draw a plane and a normal vector as shown, and redefine the following for the position vector R differentiated on u and v.
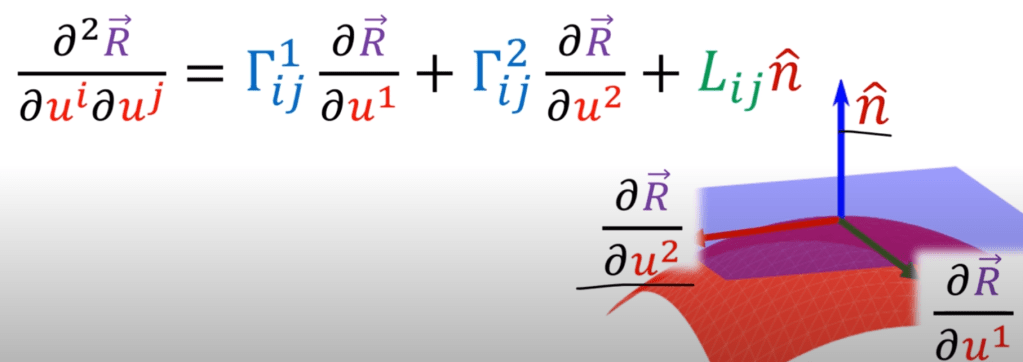
Lij is called second fundamental form, gives us the normal components, and Chrsitoffel symbols gives the tangential components of the position vector second order derivative on u and v.
Now try to solve the Christoffel symbol and Lij, the second fundamental form, we times a tangential basis vector on both sides of the equation, so make the Lij part going to zero,
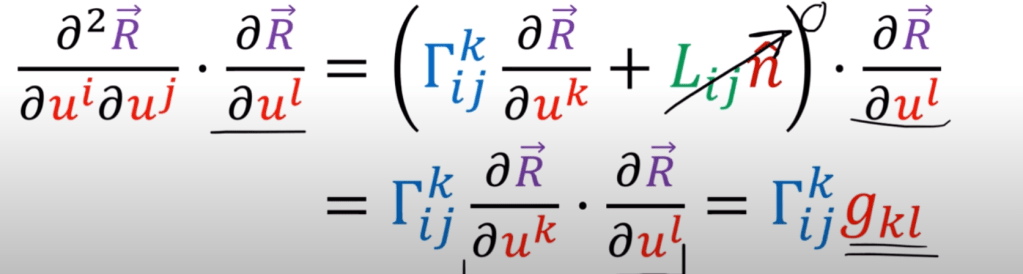
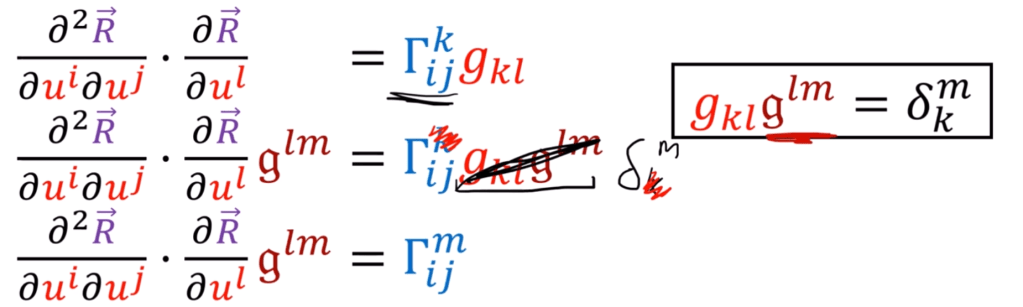
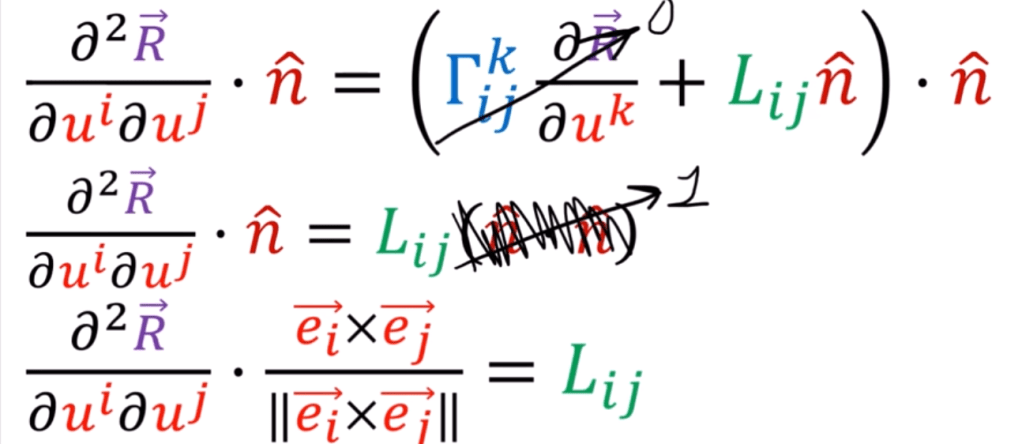
Why this hassle, it’s to find the geodesic equation:

So we can make the tangential part zero.
What is necessary is to grasp the concepts of Christoffel symbol tangential part be zero really deep! From Dr. Lia Vas’s notes, consider a surface x = x(u, v), the second derivatives are:

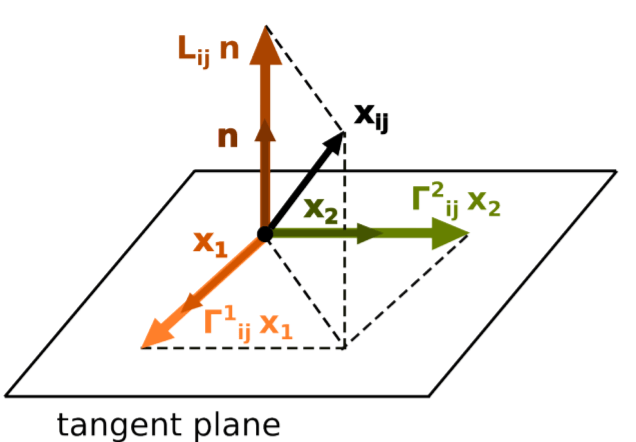
Gauss formula visualize one second derivative of Xij, it’s composed of the coefficients Γkij where i, j, k = 1, 2 called Christoffel symbols and the coefficients Lij, i, j = 1, 2 called the coefficients of the second fundamental form and corresponding x1 and x2 basis vectors.
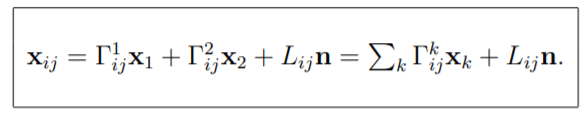
So what is the first fundamental form? The first fundamental form describes the way of measuring the distances on a surface.
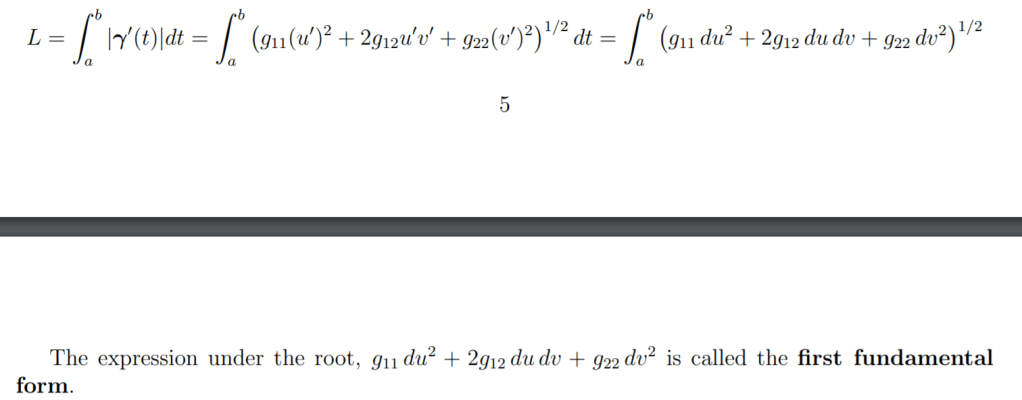
Dr.Grinfeld’s Tensor Calculus has detailed the notion of Christoffel symbol in unique way, thinking about the Christoffel symbol is the component or coefficient of the vector in the left side expressed by component times the base vector.

It can be converted to this too

Using a polar coordinate system as an example to further illustrate

Above deduction is all done by Dr.Grenfeld by his intuition or knowledge, hard for me to conceive, by referencing eigenchris’s series, a rigorous process is provided to get
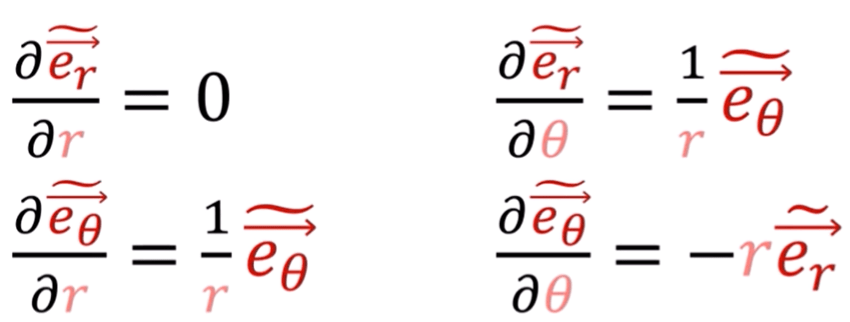
Christoffel symbol should read in order Christoffel k, i, j, meaning the component or coefficient of the partial i partial j on the k direction. Its essence is to line up with the directional basis vector ek to form the covariant derivative or directional derivative as pasted:
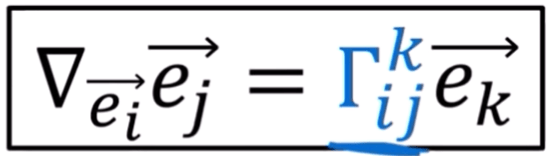
If that is too much to grasp, let’s dive into the concept of principal normal, R(s) vector T(s) vector, N(s) vector…


What’s the purpose of going through so much pain to come up with these Christoffel and lambda and normal etc.? It’s to find the geodesic curve in curved space!

As is highlighted in light green box, geodesic equation requires the part to be zero so the tangential acceleration is zero. only part left is the normal acceleration. Thinking about a real life example – driving an airplane above the earth how to take the shortest path (maybe not the shorted but the squarely straight path)? Let’s work on two examples.
First problem to solve is to find the straight line on a flat 2D plane.

The Christoffel symbol is zero in below equation
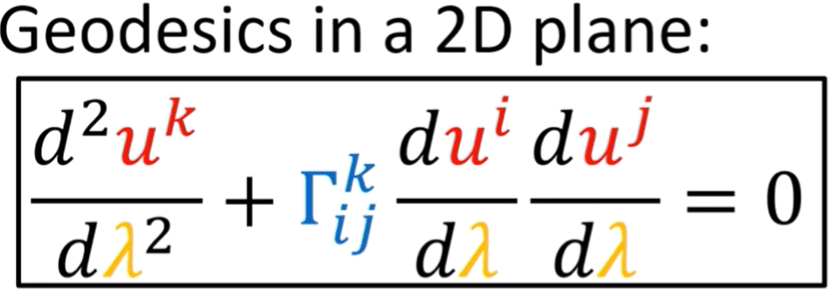
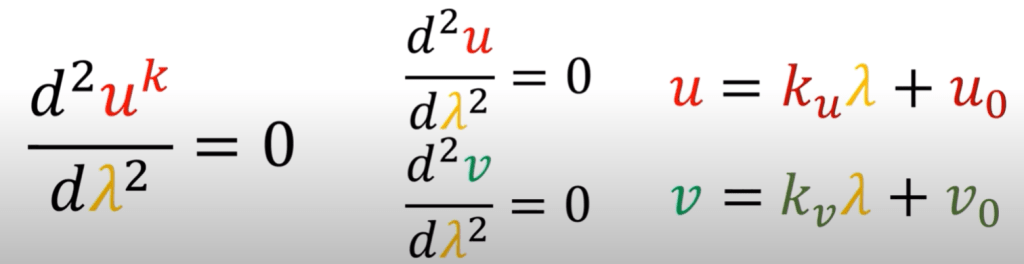
so the final solution is
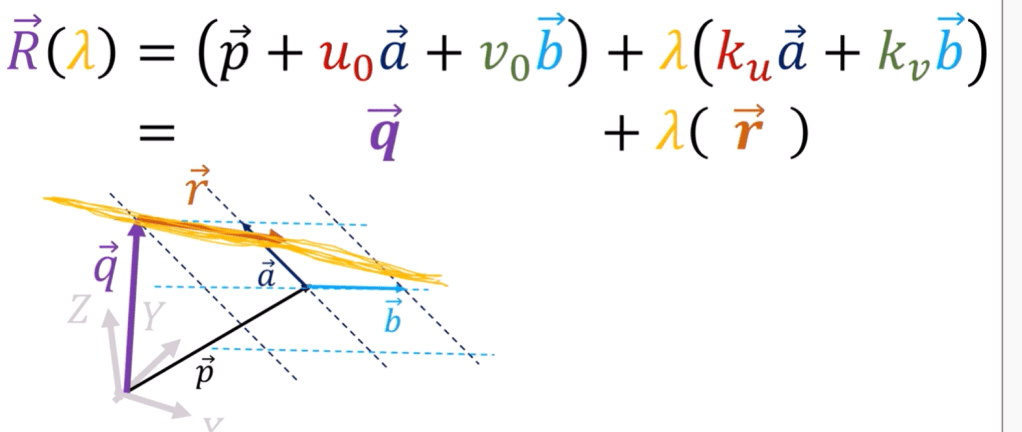
Second, let’s find the geodesic/straight line on a sphere.

So we can prepare the needed computation as follows
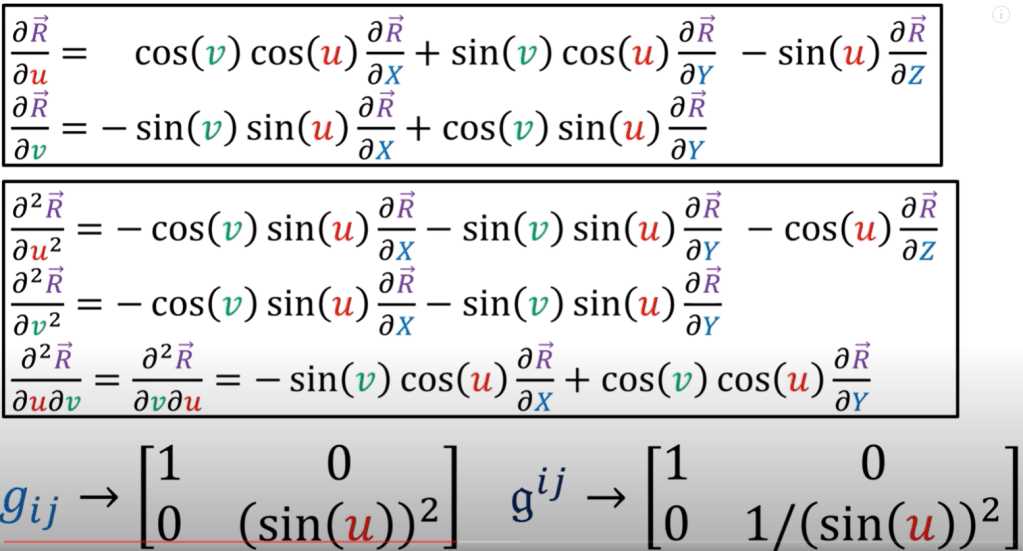
then we reach