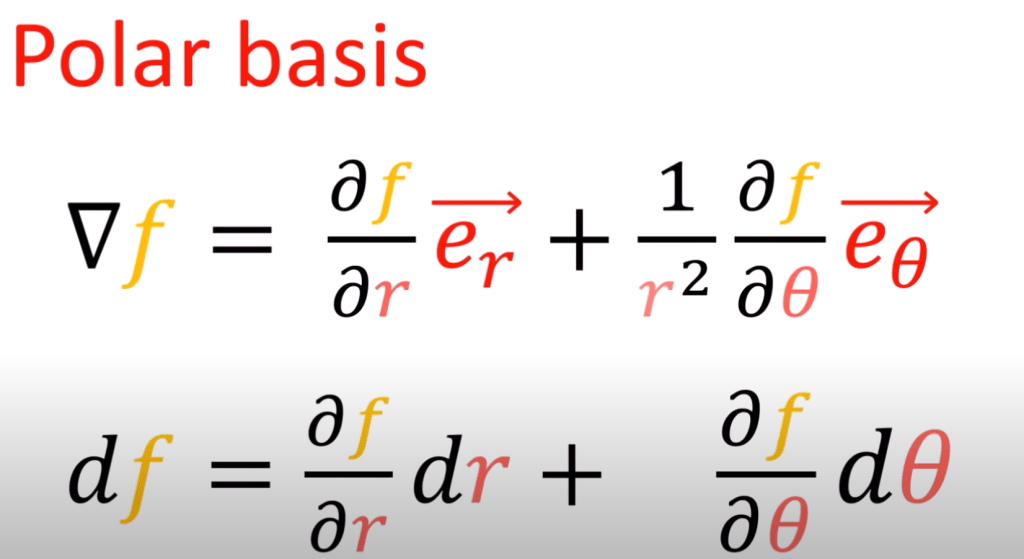- Differentiating displacement to a scalar such as time gets vector – velocity, this velocity vector can be further differentiated by the same scalar time to get acceleration etc.; differentiating a scalar such as temperature to displacement in a room space gets gradient; both are vector but different in this sense. Differentiating a vector to another vector can also get a new vector.
- Basis vector is defined as the derivatives of position vector R to the directional/axis vector (u or v, x, or y or z). If it’s normalized to unit e vector then it’s length = 1. Why?




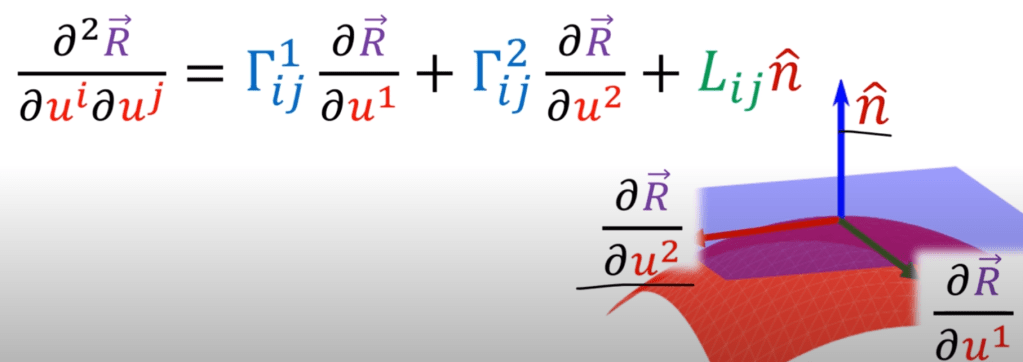
3. Differentiate these concepts: g metric tensor, kronecker delta, identity matrix, Jacobean matrix from simple to difficult
kronecker delta is identity matrix, the former is a good notation to express the latter
Jacobean matrix
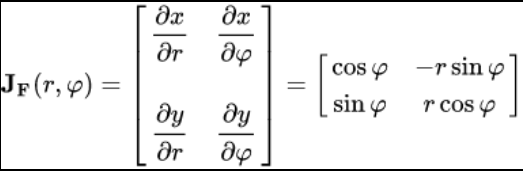
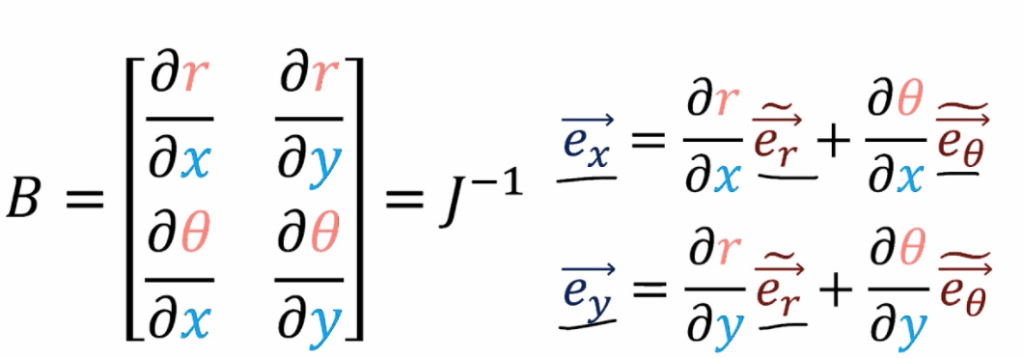
Jf Jb = identity matrix.
Cartesian coordinates, metric tensor is identity, however,

note
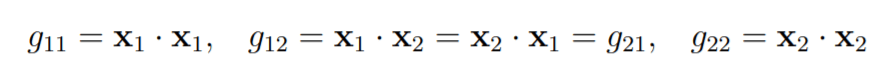
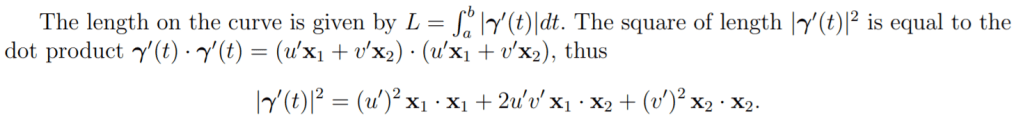
in polar coordinates, different story, for example the below is the metric tensor of polar system and of Einstein’s GR equation.

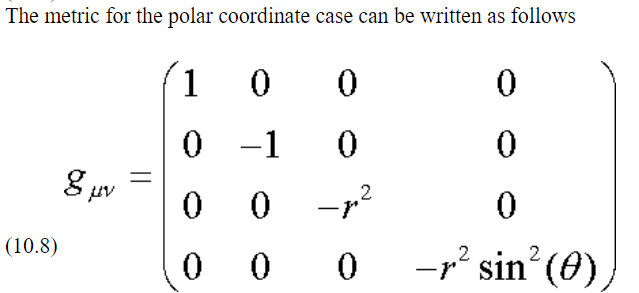
In the end, it’s worthy to grasp the definition of basis vector, using polar system as an example.
Note the basis vector is defined as derivative of positional vector to coordinate, or rate of positional vector length (?) change per coordinate in polar system, er is easier in each place the value is same; while etheta is different when r change.
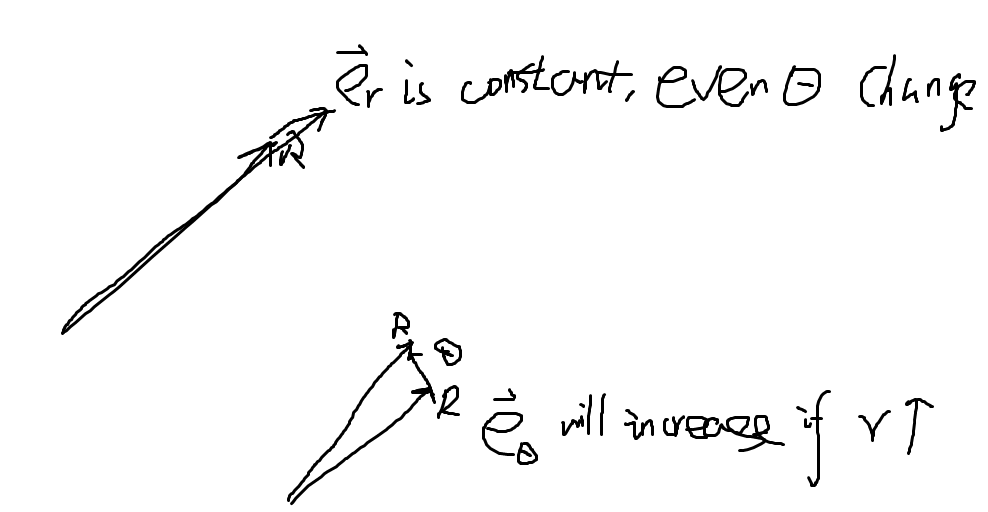
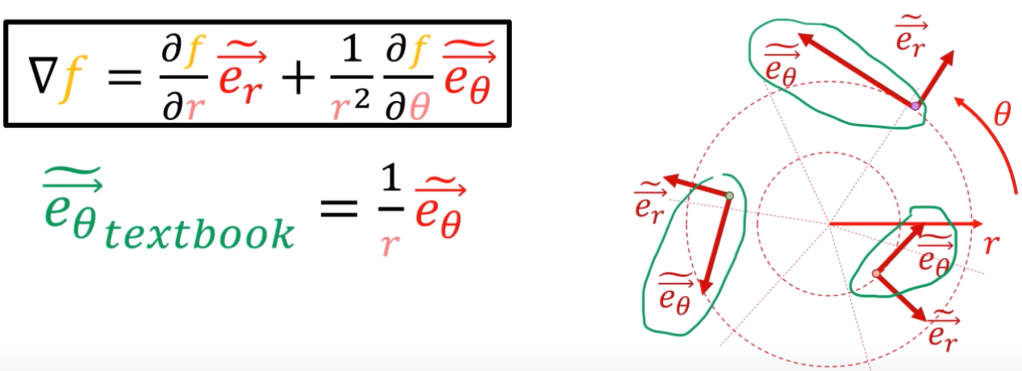
in Cartesian system, it simplifies, hence causing a delusion/distorted understanding that the below two – del f and d f are same
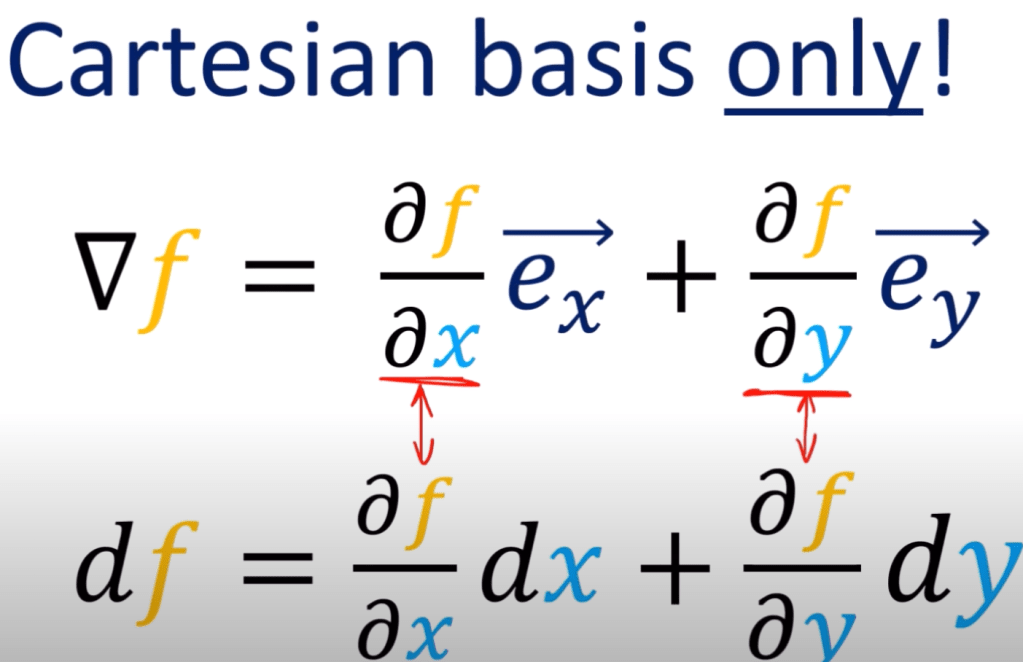
But in other systems such as polar coordinates, the covector form df is correct while pure del f(gradient) needs to be modified with 1/r2.