this is from Dr. Andrew Dotson, the clip is

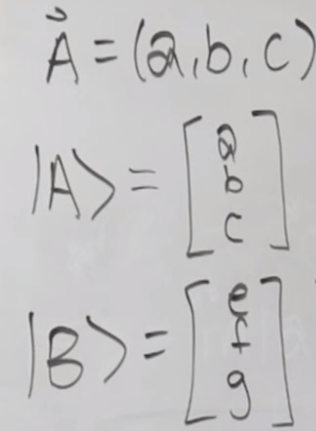
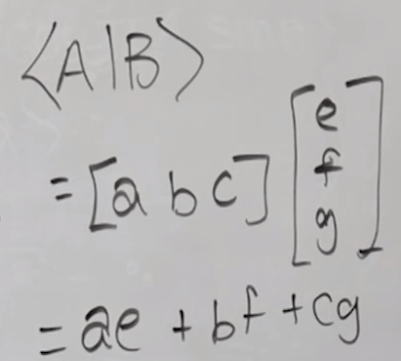
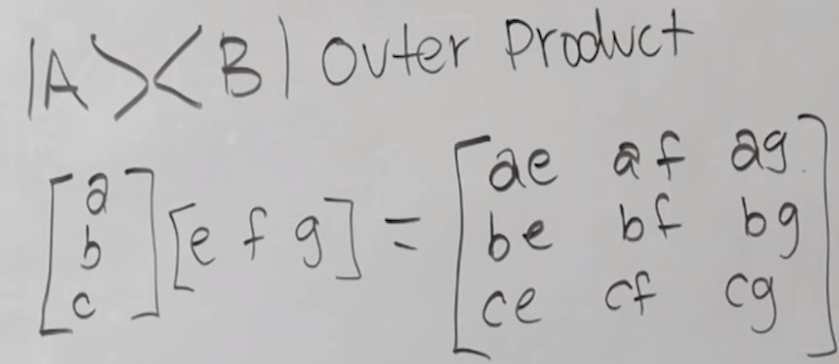
It’s natural to grasp

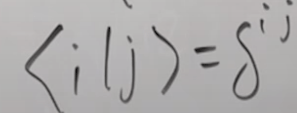
basis vector outer product each other, what is the outcome?

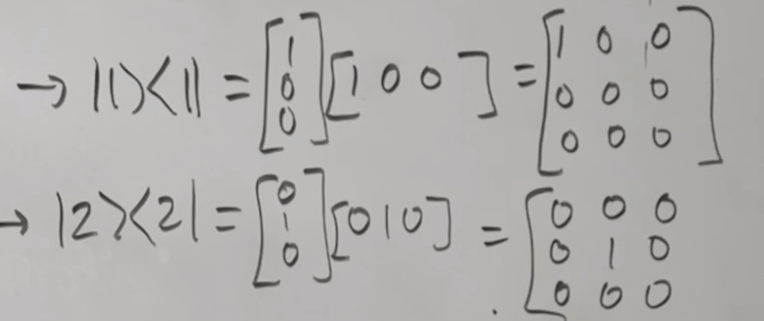
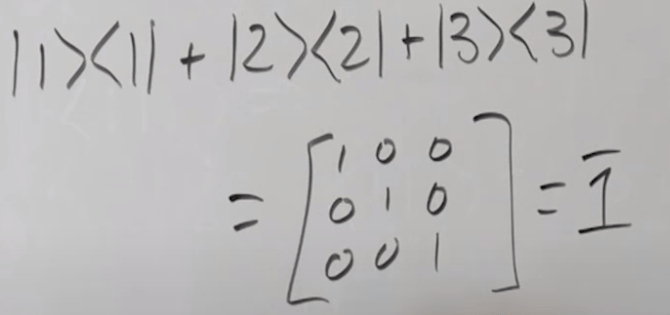
So here comes a confusion, is kronecker product from inner product above same as the identity matrix resulted from the outer product? according to wiki, “In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a generalization of the outer product from vectors to matrices, and gives the matrix of the tensor product linear map with respect to a standard choice of basis.”

Tackling the confusion, first of all, the concept of “kronecker product” is different form “kronecker delta”, what inner and outer leads to is to differentiate kronecker delta from identity matrix. kronecker delta is “The Kronecker delta is defined as : δmn={1if m=n,0if m≠n. This is equal to the matrix En which is a matrix with the diagonal filled with ones”. so I can conclude it’s same.

If we want to find the component of M at i row j column,

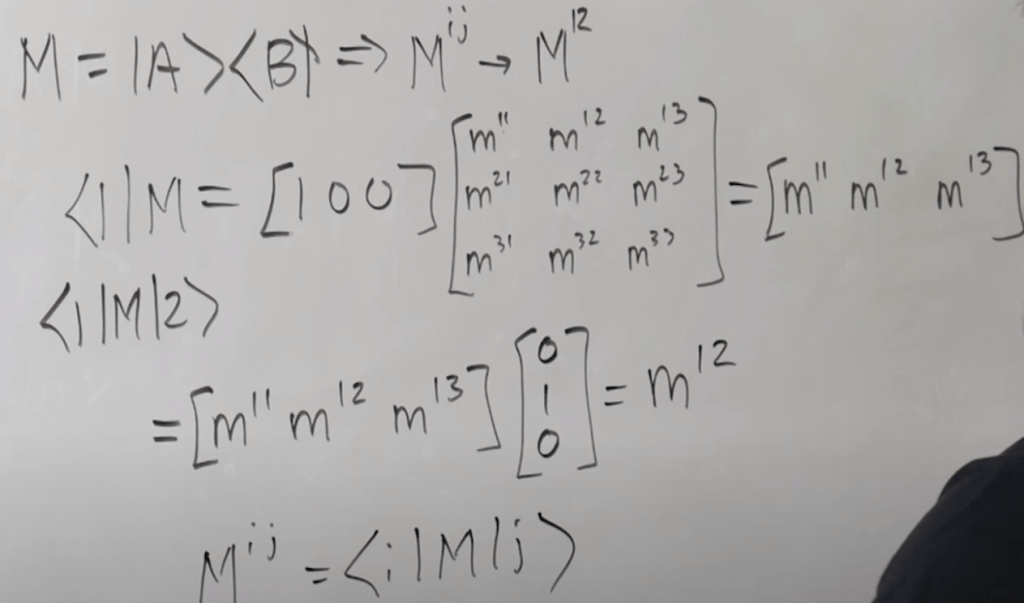
Use Dirac notation to notate any vector A as below

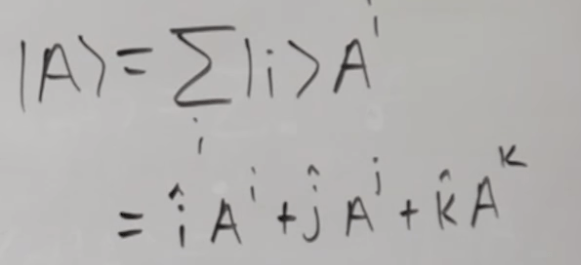
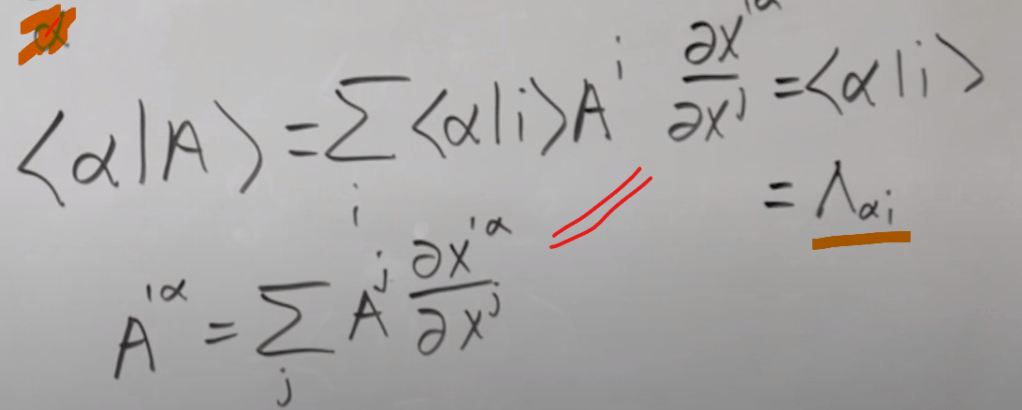
So to transform between A and A prime framework(coordinates), use