Concepts of Basis and Dimensions.

Spanning set is composed of any other vectors in the same space by any linear combination. So what is the fewest number of vectors needed in a spanning set is the largest number of linearly independent vectors. in the case of plane it’s two, and in the case of space it’s three. Hence the number is called dimension and the linear independent vectors are basis.
Let S={v1,v2,…vn} be a subset of a vector space V. The set is called a spanning set of V if every vector in V can be written as a linear combination of vectors in S. In such cases it is said that S spans V. The definition does not assume span(S)=V. If this happens to be the case, S is called a spanning set, but Theorem 4.7 does not make this assumption. In the theorem, S is just any subset of V. Consider for example S={0}, in which case span(S) is also just {0}. Or consider {(1,0)}⊂R2, whose span is the x-axis inside of the plane.

Mastering this concept so you will have intuitive/quick interpretation for the following four parts polynomials:

There are only three basis spanning R3 but four equations/vectors are given, hence one of them must be linearly dependent on the rest.

Similarly, if given the below polynomial linear system

Linear system can be regarded as vector decomposition problem, so there are three-dimensional target to be decomposed into four vectors, according to previous knowledge, chances are high that we only need three vectors to decompose, but there are four vectors in three-dimensional space, hence this system very likely has a solution and there are at least one linearly dependent on the rest.

So what is the concept of null space, according to wiki, it’s also called kernel, “given a linear map L : V → W between two vector spaces V and W, the kernel of L is the vector space of all elements v of V such that L(v) = 0, where 0 denotes the zero vector in W“, illustrated by the graph below:

Here are some more simple but edgy cases of matrix’s null space

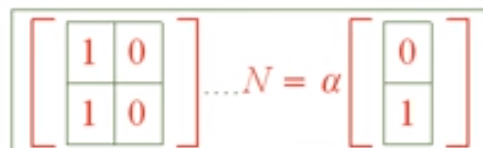
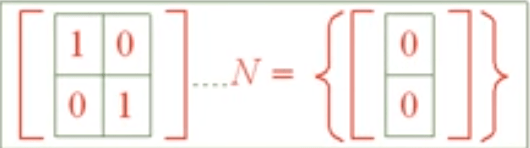
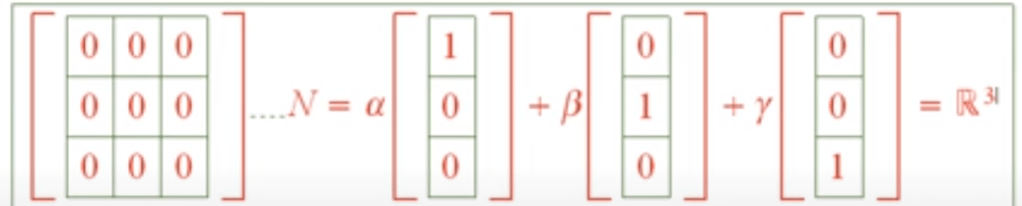
Above are some simple null space problems, mathematicians are set to solve much more complex ones. Here is a case that truly requires ingenuity: the pattern below is that if there is one column with two zeros in R3, then it’s reduced to just look at the subsquare in right bottom if there is any linear dependency, if so, the whole matrix has LD.

column space, denoted by R, as in range.
null space, denoted by N, yield zero vector to express various forms of vectors.
matrix form, denote the polynomial linear system. it’s a highly efficient form when get accustomed to it.

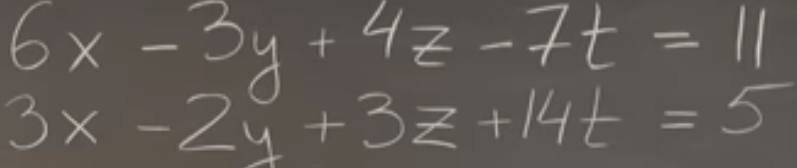
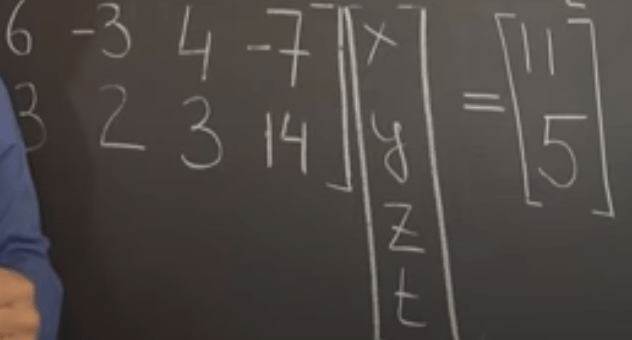
So we get used to solve linear system using vector decomposition skills with bootstrapping method

What is it to solve a tall system such as

The math intuition should come to play now that given the target in R4 while the decomposition is supposed to be done on two vectors, fanning out a narrow sub-space, the odd of that falls just in the target vector is extremely low.

What about a wide system.

It’s an opposite case that there are so many solutions. To reach to R1 with 5 dimensions available.

Another special linear system where there are zero columns

The Relationship Between the Column Space and the Null Space. Columns space the span of the columns, Null Space capture relationship between columns, If there is a 4×3 matrix, the columns space is R4, while the null space lives in R7, how do the two relate?

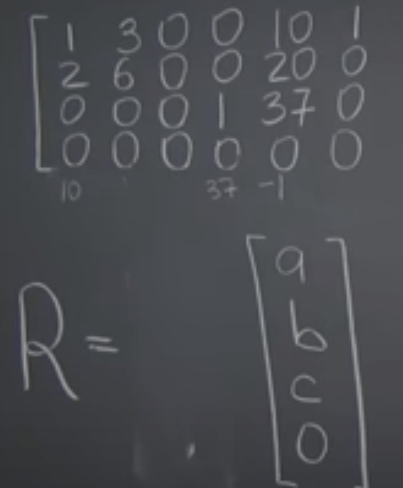
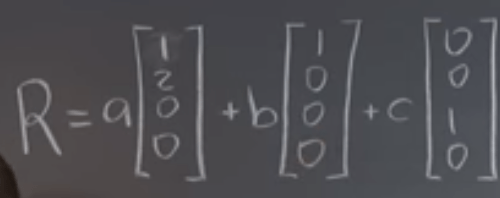
This leads to the conclusion that the dimension of column space plus the dimension of null space equals the number of columns of the matrix(? further thinking). column space is the length of the matrix(number of rows), null space denotes the width of the matrix(because it is about relationship between columns).

for example in below 3×3 matrix, it could be confusing, but lay out the expressions

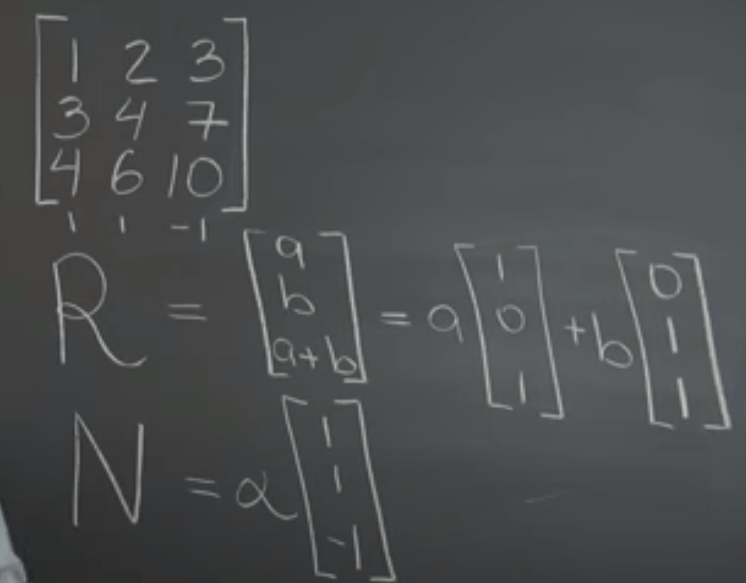
Note the notation rule in matrix, if the null space of any number it’s expressed as alpha time 1 in bracket.

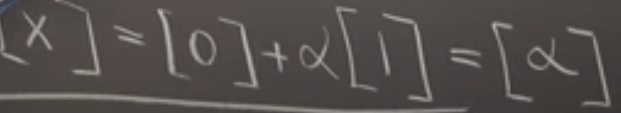
Jargon again, the below linear system doesn’t have a solution because the target vector is out of the space formed by the two columns / column space.

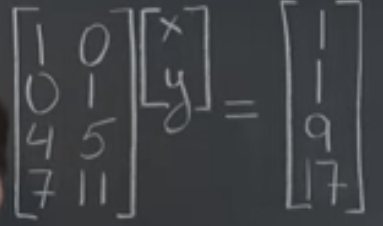
On Nov 18th, 2021 to updated/review this knowledge from Prof.Shifrin’s too. He starts from a familiar equation in elementary school, and re-expressed in linear/matrix form:

Then he went through row operations to convert bit more complex matrix into an Identity matrix times vector to be equivalent to another vector output:

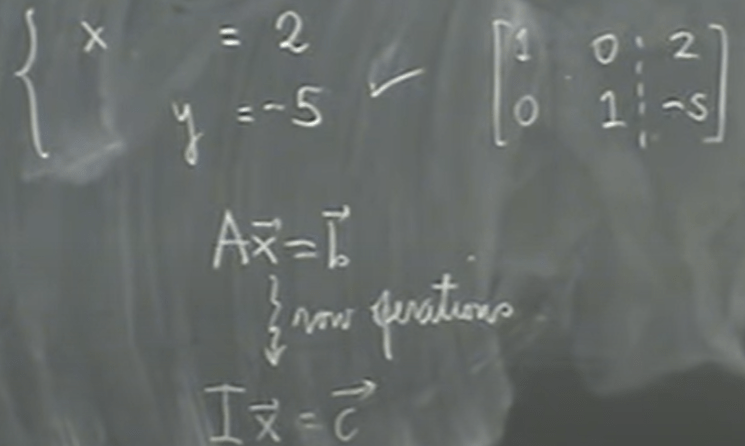
If we make the right vector output to be zero vector, it’s called homogeneous linear system. The solution involving the number 0 are considered trivial in math. The process of row operations to go from A to identity matrix I is called echelon reduction.

In vector form, the above three rows can be expressed as

It’s exactly the LA form of a line! and if we plug in the matrix A time the right part (removing the dot position of the line), we reach to the zero vector.

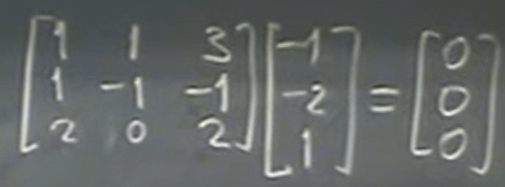
so we know X vector is perpendicular to each row in the matrix A, or

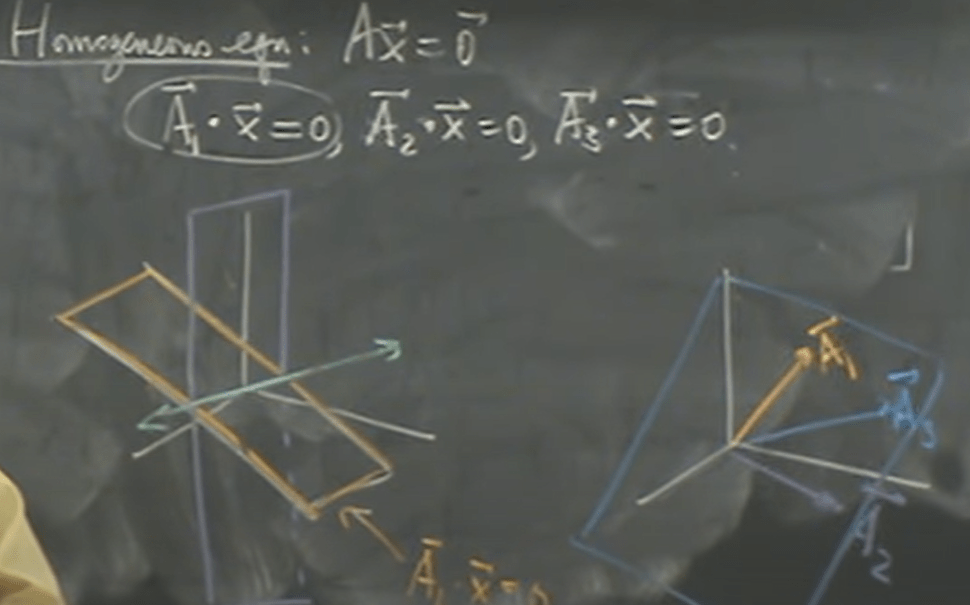
Another example:

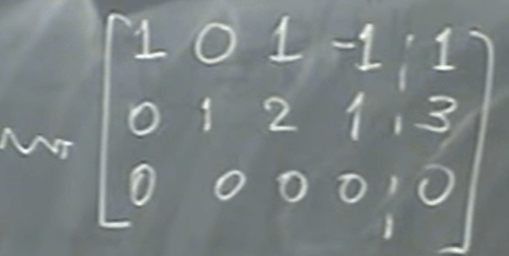
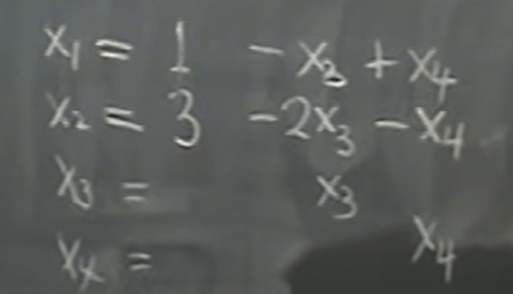
It provides a easy way to compute this x vector – note the other professor taught another ingenuine way – both are bit of tricky. This approach is more straightforward for me, be remembering the format is strict, x1, x2… is each column of the matrix A.