Gaussian Elimination is one of the most important algorithms in math, it’s aimed to solve null space (hence it preserves null space but not column space). There are basically three operations: adding multiple of one row to another (reduce one component in a row), switch rows, multiple a row by a number(reduce to simple number like 1).

Use simple example to learn how to operate Gaussian Elimination:

Strictly follow the sequence, pivot places from row 1 to 2 and so on.

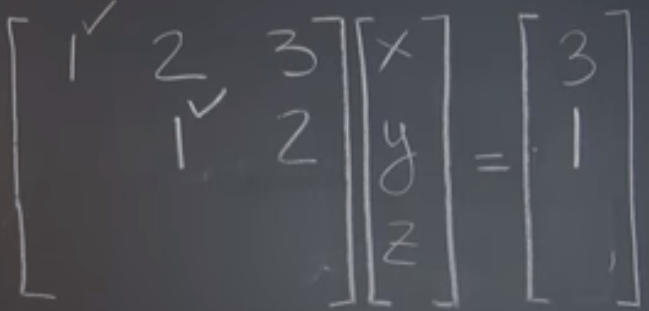
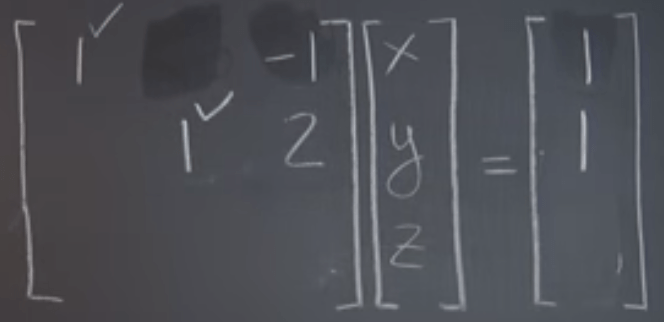
Hence the solution surfaced out clearly:

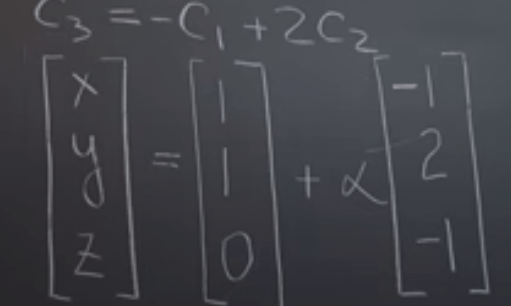
(note in practice we can march from left to right to eliminate on pivots, then from the right corner, bottom up, the final goal is to reach the Row reduced echelon form.)

For example,

Gaussian thinning: in practice, usually meticulously going through Gaussian Elimination is not necessary instead Gaussian thinning can.

Lastly do a brain twist, if knowing the null space, reversely engineer out the original Matrix.

Above null space is relatively easy to think through, what about the below one?

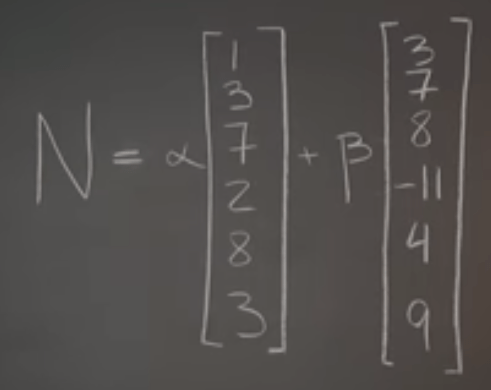
Now lots of the discussion is on dimensions(linear independency) of column space and null space. in the same vein, how about the dimensions of the ROWs? Surprisingly, the overall conclusion is that the dimensions of column space is equal to that of rows space! why? if there are a lot more columns, no matter how many more it is compared to number of rows, the linear independent columns at most is the number of rows, so it’s limited by the number of rows. Conversely, …

Hence, there derived the concept of rank, rank of columns space = rank of row space. It’s application is wide, for example

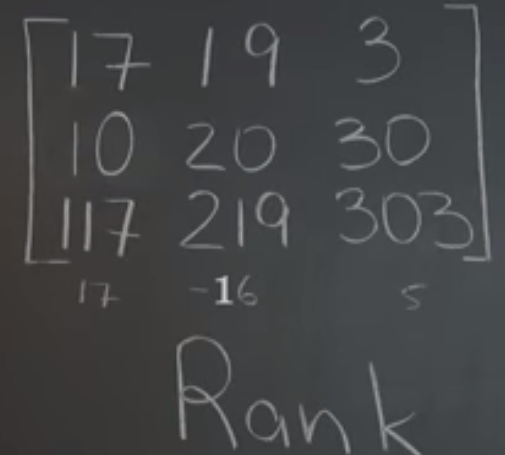
The column linear dependency is hard to see through but not for between rows.

Review this important concept of RANK by Dr.Gilbert Strang at MIT.

or another example

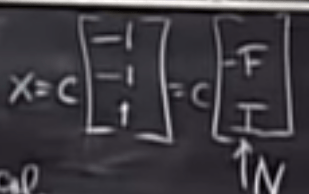
If proficient in applying RREF (Reduced Reduction of Echelon F), it’s easy to solve or find null space solution.

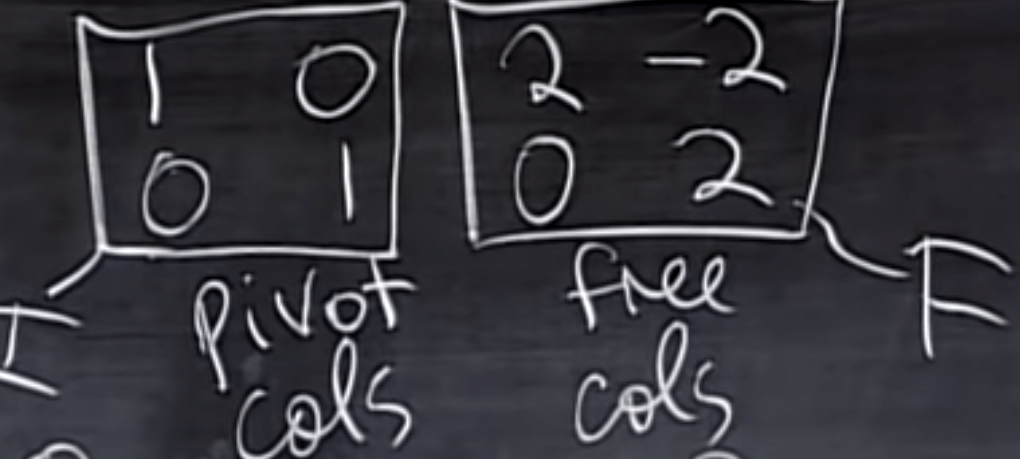
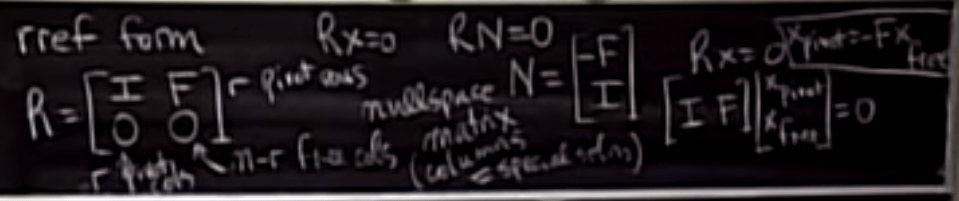
The RREF of a Matrix Whose the Null Space is Known Beforehand.

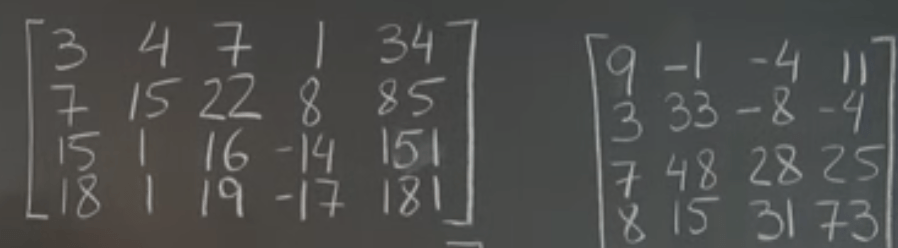
So the logic reasoning makes it easy to deduce after Gaussian Elimination