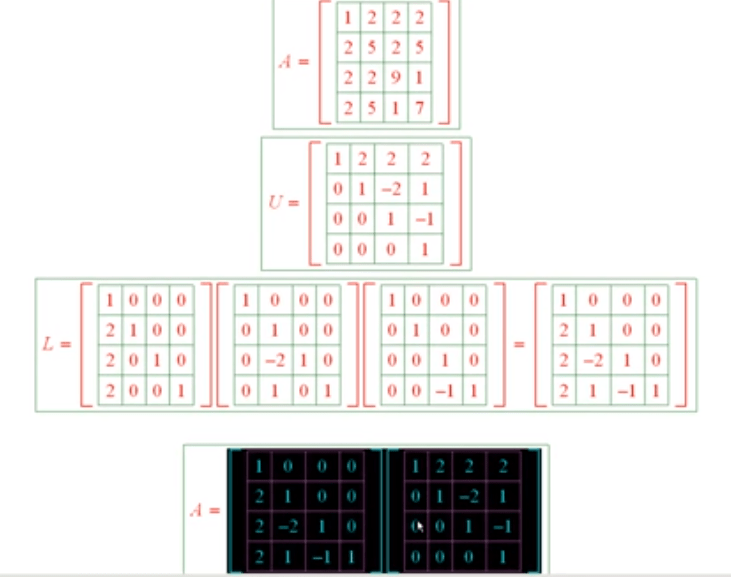
Elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation. Elementary matrices are the simple form of actions exert on the other matrix hence important.

For example for the matrix below, putting elementary matrix on the right side meaning we do the column operation: on top of the a, d, g – first column, there is 2 on the second row, meaning adding 2(b, e, h) onto the first row.

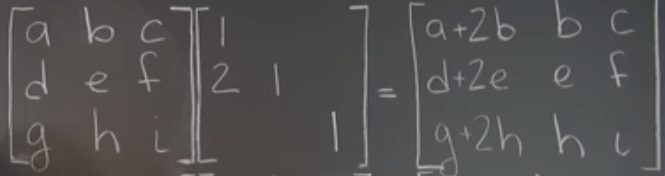
The same can be done from row operation if we put the elementary matrix on the left side.

(the thinking is tricky, as Prof.Bast said, the key is really to practice and practice)

The inverse of elementary matrix

To figure out the inverse, first say what to do to get the elementary matrix from the identity in a particular order, then reverse it in exact steps.

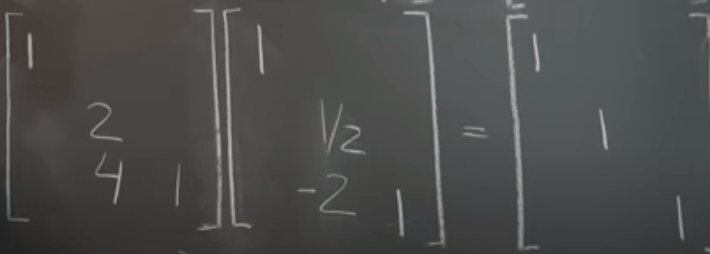
The LU Decomposition: following the above knowledge of elementary matrix, put it into usage to decompose a matrix

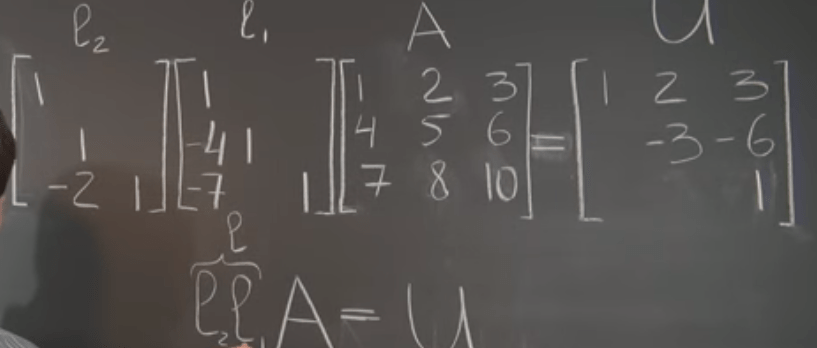
If we take the inverse of two small l product and move it to the right we get A = LU. Note when taking inverse, the sequence has to be reversed. L = l1^-1l2^-2.

An exercise example