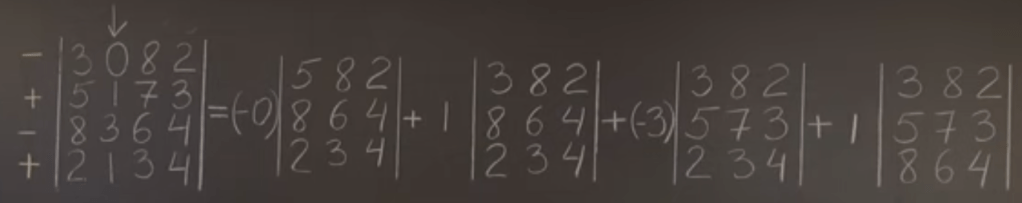We know how to tell if a matrix has linear dependent row/columns via Gaussian Elimination but it’s too cumbersome, so we then go all the way back to the original form such as below, and conclude the key is the proportion between b/a and d/c being equal.

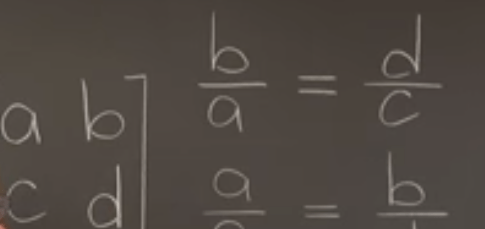
To account for situations where one or more of the coefficients are zero, ad – bc is used as a standard, we call it determinant:

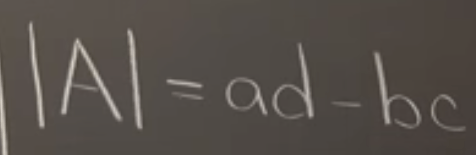
Aided with the first row of Gaussian Elimination, we can infer the determinant of 3×3 matrix, and then summarize certain rules to help memorize:, among them the Indian approach is the best

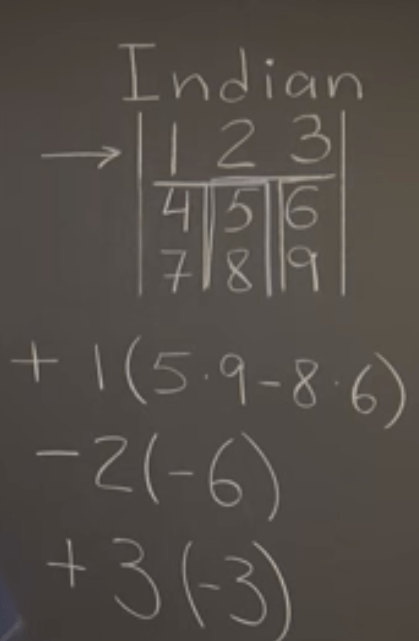
For NxN Determinant, the terms grow by factorial fashion.

The Direct Algebraic Definition of the Determinant:

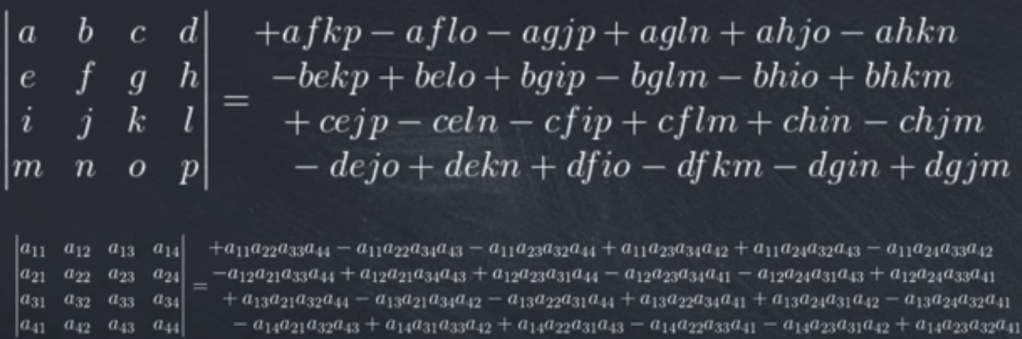
Just to grasp properties of determinant is helpful in future math computation: (note put two vertical lines around a matrix is the expression of determinant)

Transpose Matrix’s determinant is same as its determinant.

The Determinant of a Triangular Matrix is the product of diagonal terms.

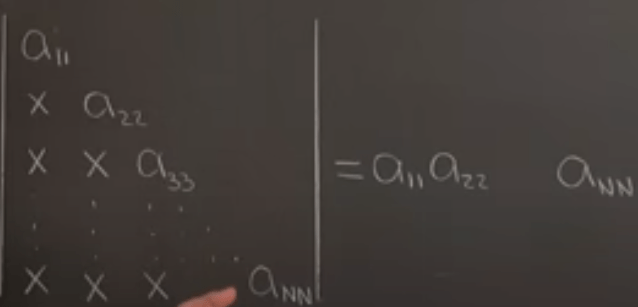
The Linear Property of the Determinant:

The Effect of Adding a Multiple of One Row to Another on the Determinant: it is same as the original matrix, proved by below combining alternative property and linear property of the determinant.

The Determinant is Zero ⇔ Matrix Is Singular (iff)

Areas and Volumes by the Determinant.

Now equipped with matrix determinant theory, we can use it to prove common formulas we learn in elementary schools, such as Determinant-Based Derivation of the Triangle Area Formula:

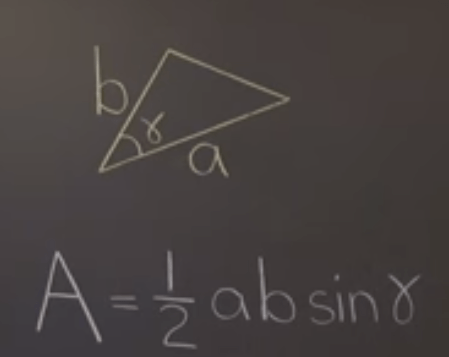
Proving by drawing vectors and then conduct matrix calculation-determinant

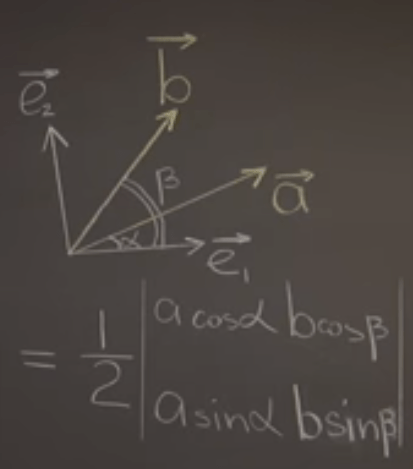
There are a spate of such application, giving glimpse of algebra power. Another example is to figure out the area of the triangle. The LA expert can list the matrix A below to represent it and easily deduce the area.

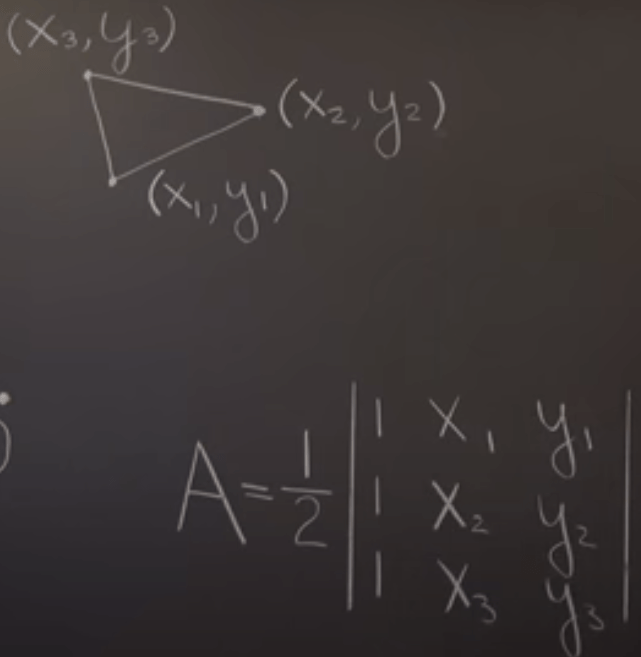
Transforming a matrix by another matrix, the net outcome is basically multiplying the determinant by the other matrix’s. To prove, simply applying the linearity, alternative property in conjunction with the “elementary matrix” operation.

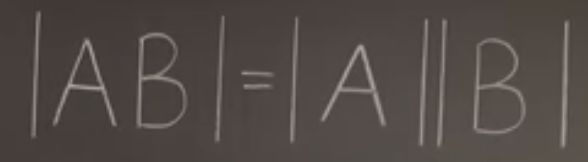
There are three elementary scenarios:

1. multiple a row in the A,
2. switch rows/columns
3. scale up a row/column

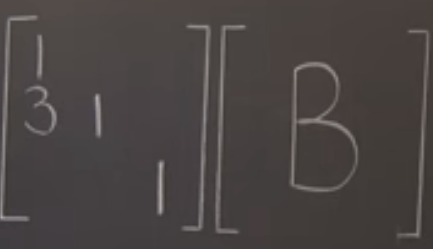
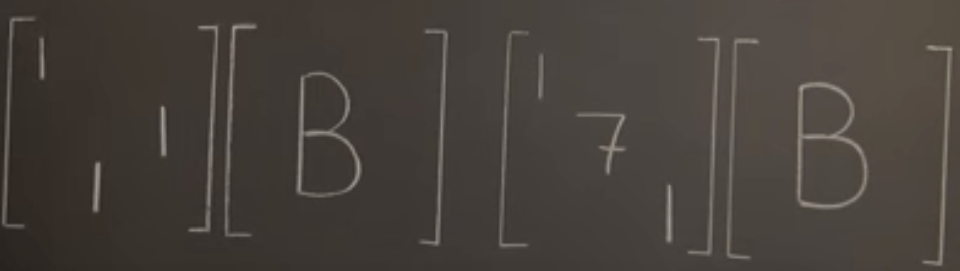
Since every matrix can be represented by multiple elementary matrix, hence what proves to be true above can be extended to any matrix A, acting on matrix B.

The Laplace expansion is a formula that allows to express the determinant of a matrix as a linear combination of determinants of smaller matrices, called minors. The Laplace expansion also allows to write the inverse of a matrix in terms of its signed minors, called cofactors.