There are various transformations: reflection and projection. They have the vector on the borderline and on the vertical position as their eigen vector and eigen values respectively. Note zero can never be the eigen vector but can be eigen value. If a vector is reflected twice the result is original vector itself, hence R^2 = I; projecting a vector twice however does nothing, so P^2 = P.

Rotation is another kind of transformation, RalphaRbeta = R(alpha+beta)

Transformation occur in Space, As Opposed to on the Plane, if we look at the reflection transformation, there are three eigen values (1, 1, -1) with a pair of 1s to reflect the whole plane. Similarly the projection of a vector in space is linear and the corresponding eigen value is (-1, 1, 1).

Derivative also is a form of transformation.

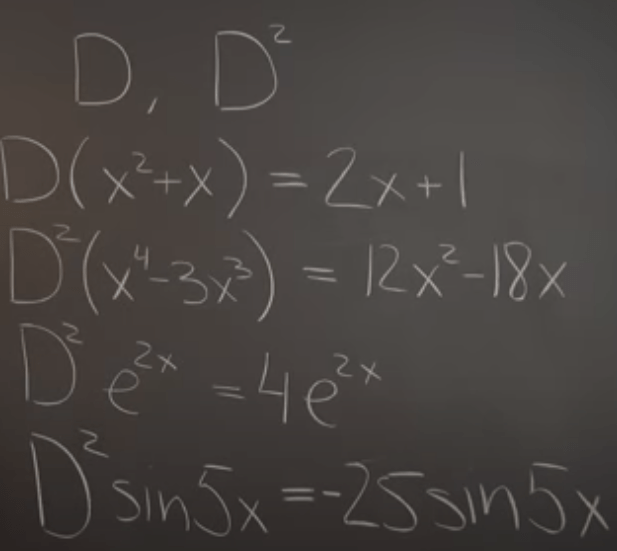
Then what are the eigen value and eigen vector? There are two special functions: e^x and sin(x).

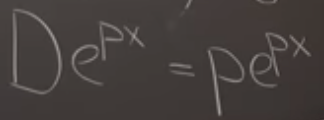
Dilation as a form of linear transformation has wide application in wave equation.

from vector to functions/polynomials now to Rn, let’s find the linear transformation of Rn, and if so, what are the eigen vectors and eigen values? For example, this transformation – switch the first and second row, double the value on the third row,

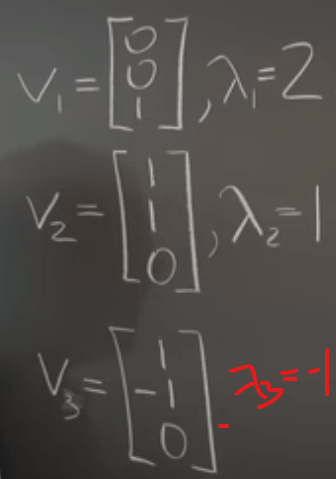
by eyeballing, inferring we conclude it’s a linear transformation, and there are three eigen value/vectors.

Another example like below

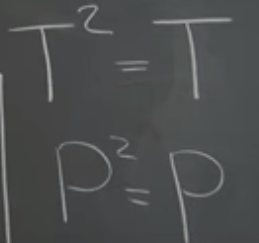
Reaching to a conclusion that all linear transformation in Rn can be represented by matrices, vice versa. The above examples can be expressed as

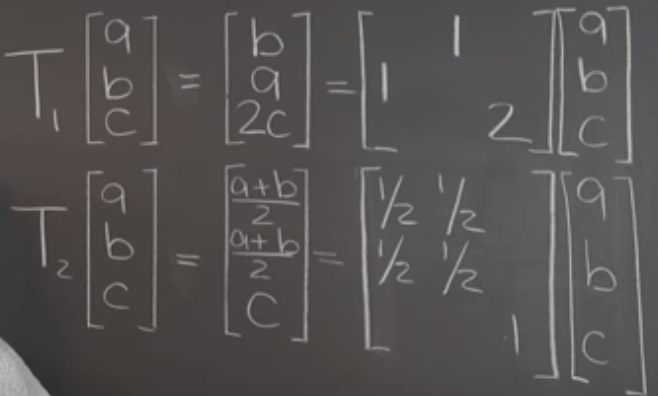
Grasping concept of linear transformation we notice each time we’ll be asked to find the eigen vector and eigen value, why are they so important? It turns out they are the bare essentials for LT. In choosing basis we will rely on eigen vectors, for example, there is a vector V, and another matrix T, V can be expressed by the following alpha time e form, as a result, the eigen value being inserted so we can interpret any matrices such as image interpretation.

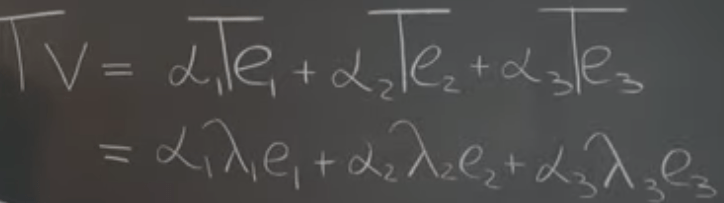
Switching the gear to find the null space of linear transformation, going through what discussed above, we realize that for projection transformation, the vertical vector is in null space; for first order derivative, the constant function is in null space; while for second order derivative, the linear function is in null space.

Then moving to the linear transformation on Rn or a vector by a matrix, what’s the null space of this matrix? as shown below, simply we put zero vector in the right side.

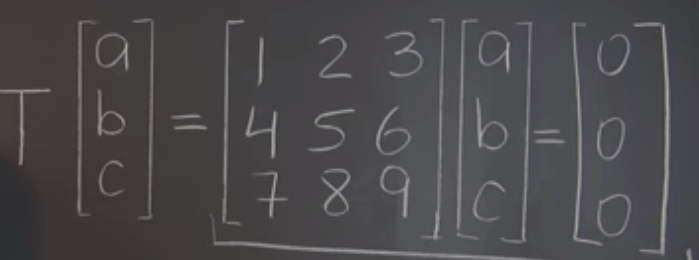
Inverse of linear transformation, we focus on the matrix as transforming, using the below deducing/reasoning, we can say the inverse of T on v is equal to the inverse of A multiply v. Note that A or T can not be in non-trivial null space or it will be noninvertible. Conversely, if there is no non-trivial null space it is invertible. (no inverse, meaning multiple vectors can be transformed to the same vector, then one can infer the delta between these former vectors time T = 0, proving they are in the null space)