In previous blogs, we found the importance of eigen vector and eigen value but the method to find these values are not systematic or algorithmic, this chapter is to tackle this problem starting from a simple formed problem:

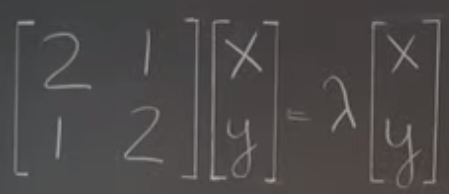
Following the elementary level way to convert to polynomial and then convert back to linear algebra form like below

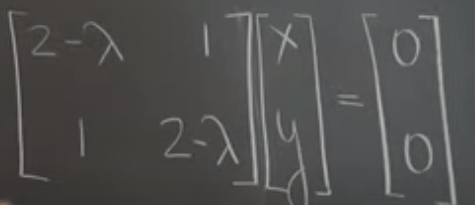
The problem now is to find lambda values that makes the left part “linearly dependent” or “singular”. Then we can compute “determinant” to make it non-linear.

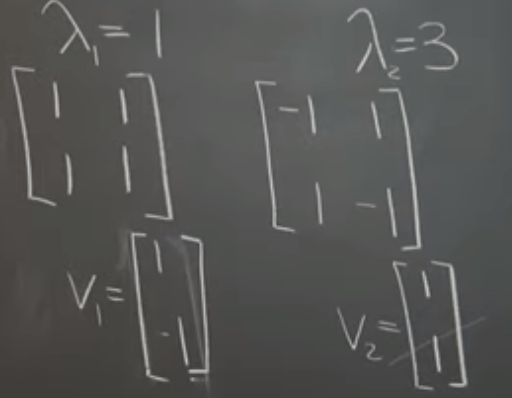
Algebraically we can derive the same as

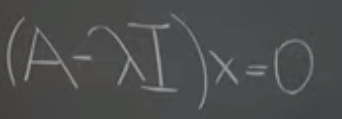
In calculating eigen values, we found that The Sum is the Trace and the Product Is the Determinant of the Matrix, which can be proved in a rigorous way.

A and Aᵀ Have the Same Eigenvalues. Because the very definition of transpose is that the diagonal values are same while the rows and columns reflect each other.

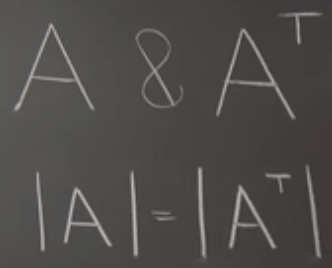
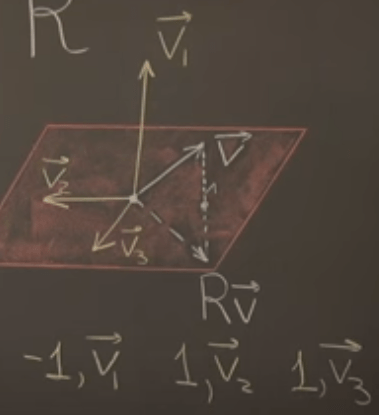
Repeated Eigenvalues and the Geometric Multiplicity. Under what circumstances will the eigen values repeat? One example is the reflection upon a plane

Or the reflection upon a line

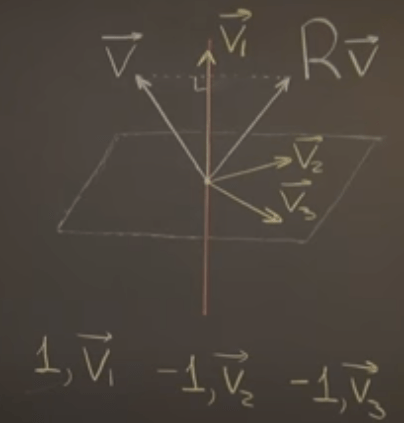
In Rn, the circumstance can be shown as this example

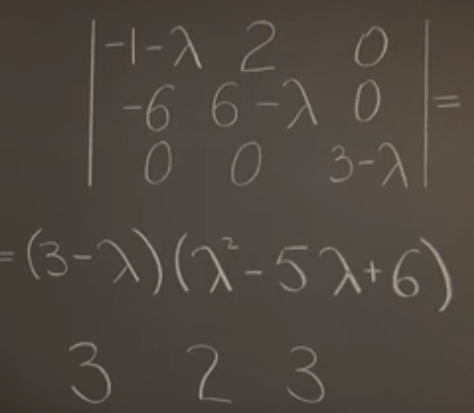
There are two repeated eigen value 3, it’s called the Algebraic Multiplicity. Plug in the lambda 3, the matrix has two linear dependency or null spaces terms, hence it seems this is consistent to the former geometric multiplicity.

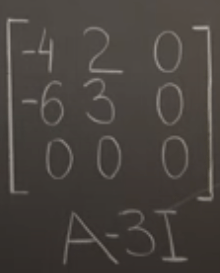
However, it could be algebraic multiplicity exceeds geometric multiplicity, for example,

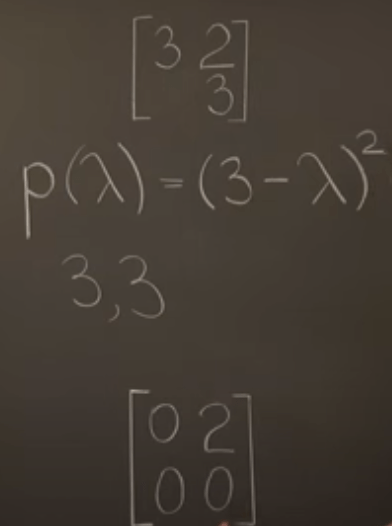
This repeat value in diagonal position matrix has two same eigen values 3, but the eigen vector is only one, meaning the algebraic multiplicity is two while the geometric multiplicity is one. This kind of matrix is called Defective Matrix.

Note defective matrix could take the form of repeated diagonal, with upper space filled with some value kind of matrices, it can also expressed in the below format. Further defective matrix is very fragile in the sense that a tiny perturbation will cause dramatic change from defective to normal matrices.

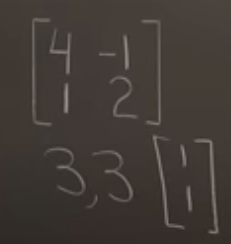
At a glance, it seems defective matrices have a huge flaw that they don’t have enough eigen vectors so hard to find basis, here is the solution. The matrix’s eigen vector can be in column space and further down until find three vectors in corresponding to the three identical eigen value 3.

We find [1,1,1], this column in the null space of this matrix, we look for a vector that is in the kernel or null space of this linear transformation. this vector is also in the range of the linear transformation. Generalizing it to polynomial etc…

Next, let’s explore if A squared or A inverse has eigen value and vector?

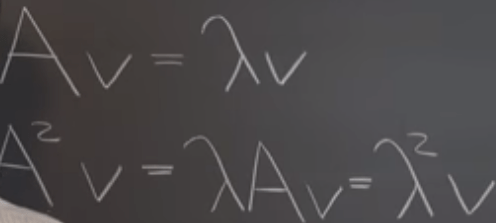
Generalizing, any power of A can be applied in the same way. What about the square root of A? it seems problematic at the sense that one value can have multiple value taking square root? (later on)

And explore similarity transformation, the eigen value of XAX^-1 is same as A, while eigen vector is Xv.

To deduce, let’s assume B = XAX-1, knowing the lambda, v of A’s, assume there is a vector u = Xv, then plug in u to B, because inverse X and u is v, so we get XAv, according to definition, Av = lambda v, so move lambda ahead, we get lambda b. proved.

Every Matrix Satisfies Its Characteristic Equation, which is replacing the lambda in this matrix’s characteristic equation with the matrix itself, the equation still holds.

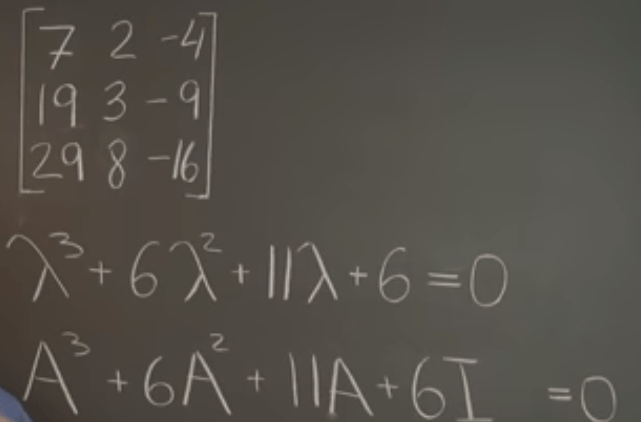
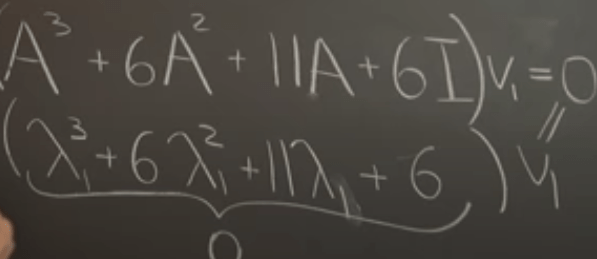
For defective matrices, or matrices with repeated eigen values, above theorem still holds.