The most easy form is diagonal matrix, the eigen value basically is the value in diagonal position and the eigen vector is corresponding basis vectors. Less easier is the case where there is a single non-zero value in diagonal line. We can infer this value is one of the lambda and the null space of that column.
If there are Equal Sums of Rows or Columns,
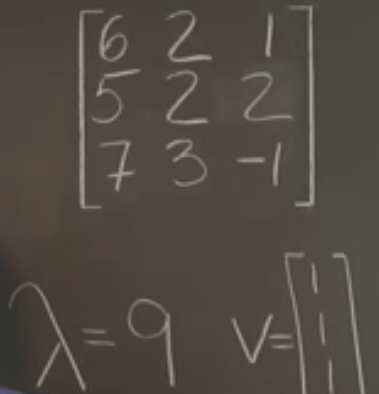
If there is equal sum of rows, at the premise (deduced before) that the transpose of the matrix has the same eigen value of the matrix, we can at least find out lambda is the multiple times which we get the sum of rows. Eig
Nontrivial Null Space, since we can identify the linear dependency between columns, we know we can appoint lambda = 0, and the null space components as the eigen vector. for example

Similarly, the determinant like trace, can also help find eigen value and vectors. So is transpose helping.
The Block Diagonal Structure:

Finally, to learn all these tricks of finding eigen value and vector, what’s the purpose? can we go reversely, meaning from known eigen value and vector to restore the original matrix? At least for the simplest form – diagonal matrix, it’s easy to restore; then the similarity transformation of the D matrix, since v = Xu, we can deduce the eigen vector is the columns of the X, while eigen value is same as D.
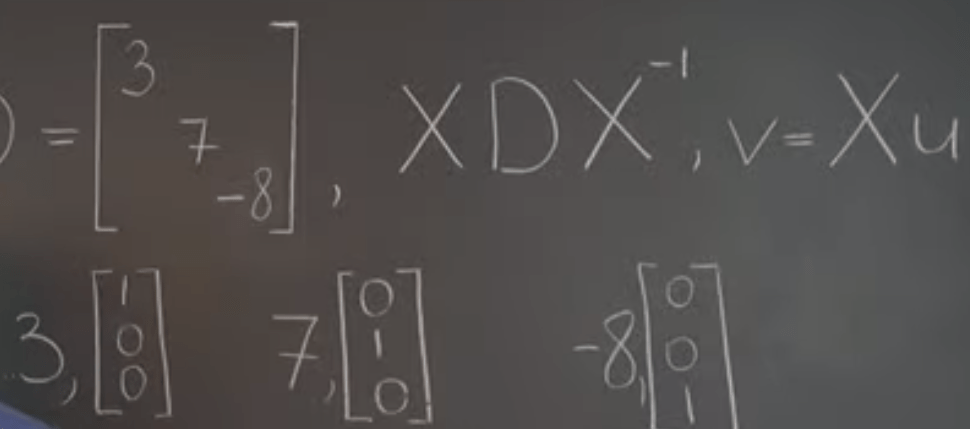
Note a similarity transformation is B=M−1AMWhere B,A,M are square matrices. The goal of similarity transformation is to find a B matrix which has a simpler form than A so that we can use B in place of A to ease some computational work. Lets set our goal in having B be a diagonal matrix (a general diagonal form is called block diagonal or Jordan form, but here we are just looking at the case of B being a diagonal matrix).
Eigen Value Decomposition: From what learned above, the concept of eigen value and eigen vector, we know if A is

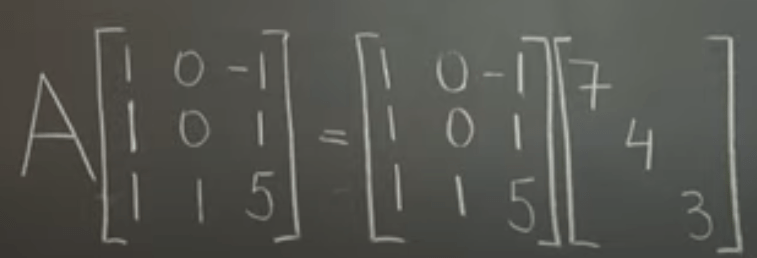

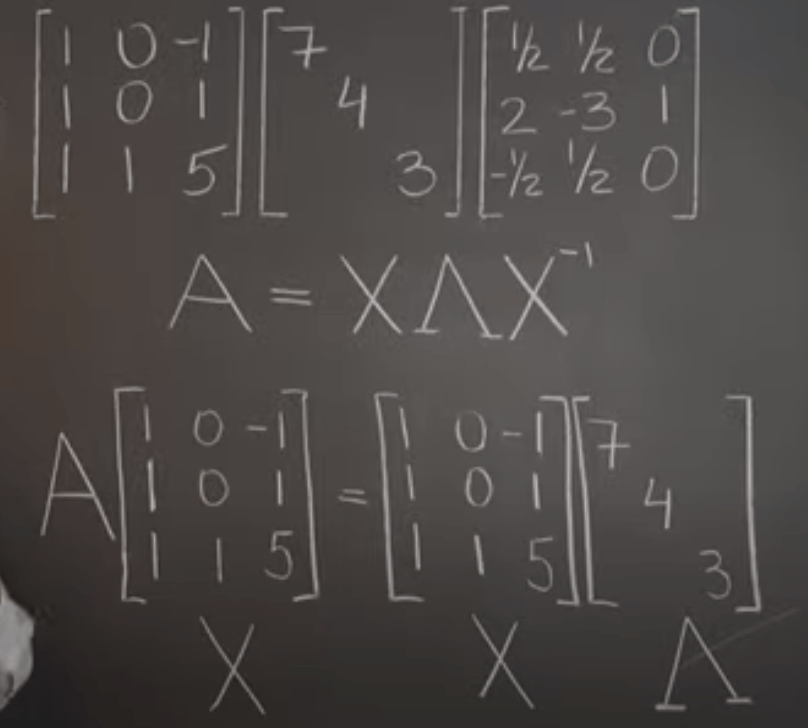
Why taking that much trouble to perform the eigen value decomposition? The overarching purpose is to restore the original matrix A based on eigen value and eigen vector and the very first question is “is it in the first place restorable?” The answer is yes, there is only one restoration. There is no information loss.
Why we need to restore the original matrix?

A inverse, even A raised in natural constant, any power, or sinA …. all can be derived in similar fashion. The power of this eigen decomposition is incredible.
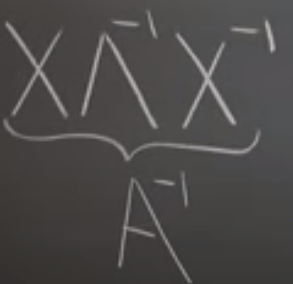
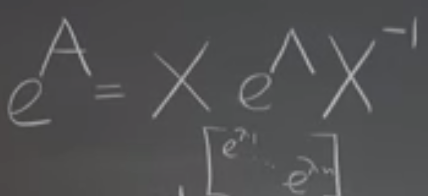
The glorious application of eigen decomposition in Fibonacci Numbers:
The ingenuity here is to transform the rule into LA format:


