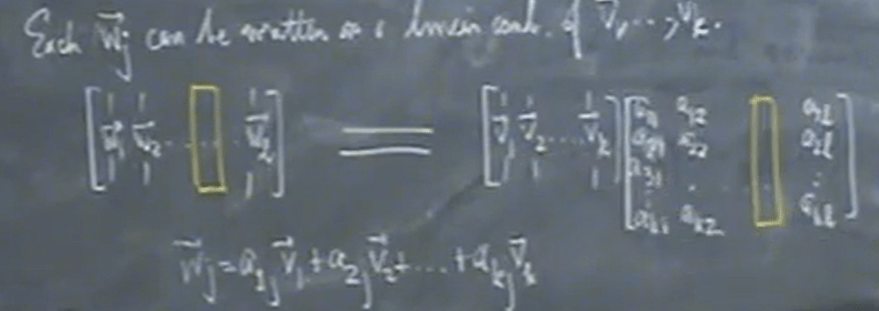LA is powerful especially in computer era now, so what we will do is to decompose complex problem in component spaces, solve it and revert back to original form – solution.

Even troublesome it’s straightforward to convert vector, polynomial and Rn to basis system, then let’s try to do the same for linear transformation, starting from the simplest reflection transformation:

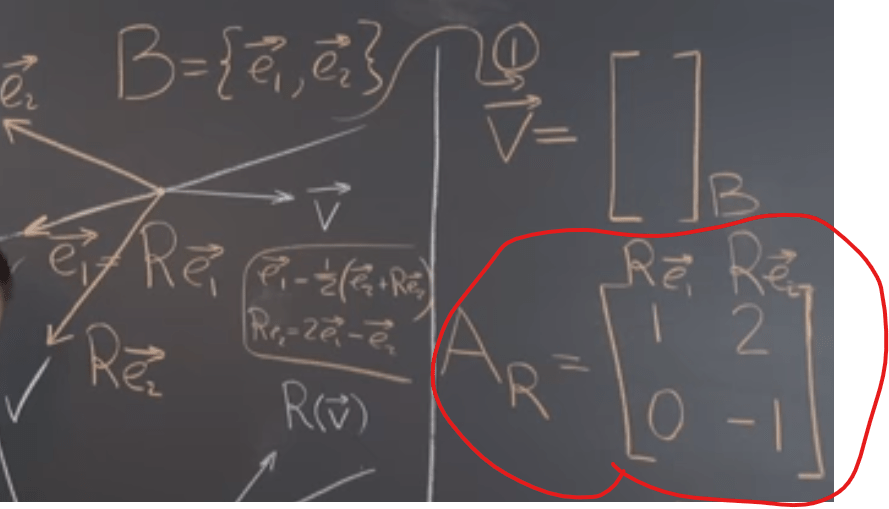
The beauty is that if we choose different basis system, the reflection matrix Ar or Rb(later on the author change the symbol, stating Rb is more accurate), for example, here is a new basis system F instead of B:

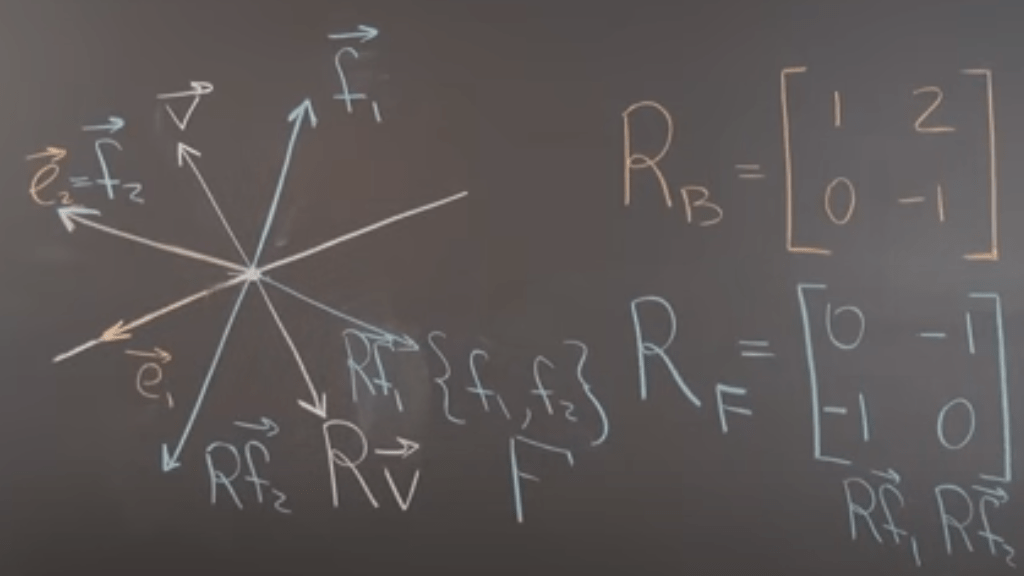
Taking polynomial to study this “trick”, what if there is such a linear transformation

What if you are supposed to solve this polynomial using the colored basis system:

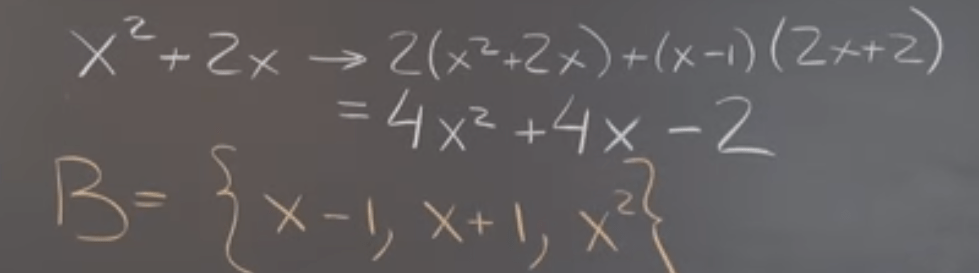
Now taking Rn to rehearsal again:

For example using this basis system:

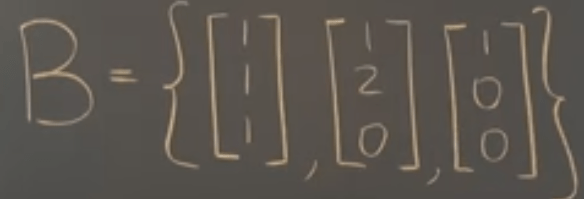
There are various LT matrices given various basis you choose

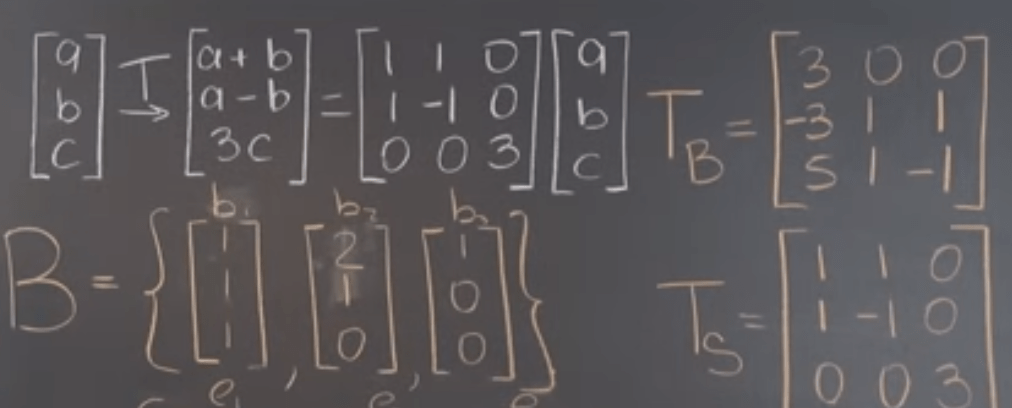
What if we use the eigen vectors as the basis,

The corresponding T matrix is the eigen values in diagonal form.

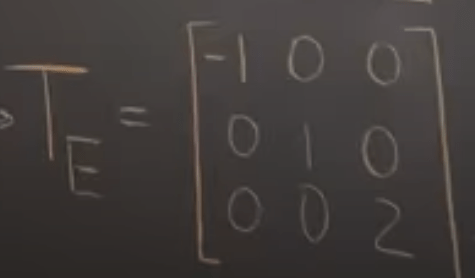
Proof that Eigenbasis Yields a Diagonal Matrix: it is quite intuitive and direct per eigen definition

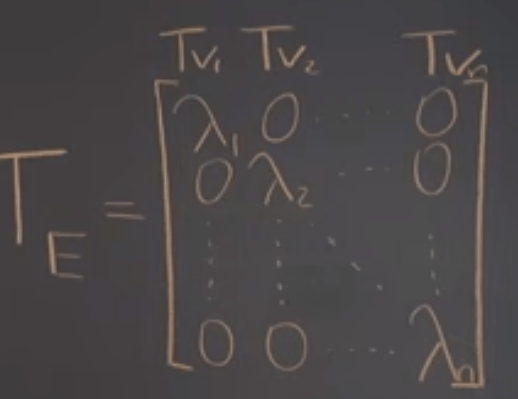
Lastly, even non-linear transformation can be represented, Represent Nonlinear Transformations by Matrix Products, there is some tricks to be applied, taking the following translation for example

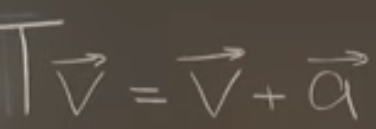
adding a tail of 1 would accomplish

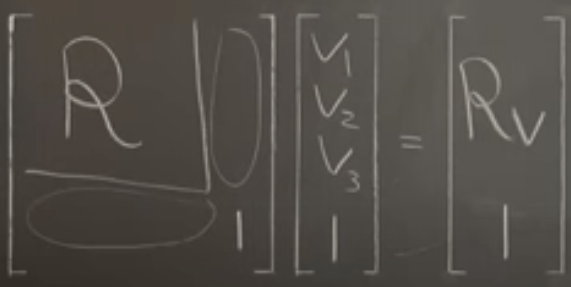
Now you need to come up with the matrix representation of a rotation in alpha vector distance:

It’s clear that the component is equivalent to the eigen vector no matter what basis system you choose. Given this knowledge, know we can tackle the Dilation transformation such as below. Because we can easily figure out the component and hence the eigen value and eigen vectors, and finally converting back to the polynomial forms.

Give the basis system to be {1, x, x^2}, the eigen value and vector are

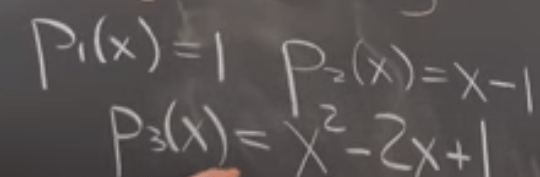
On Nov 2021, inserting in deeper understanding about subspace, dimensions according to prof.Shifrin,

It’s vital to write this automatic obligatory sentence that suppose c1w1 + … + ckwk = 0, we say that if c1 = c2 = … =0 makes it the most efficient. Hence it’s easier to understand/prove the theorem:

Suppose {v1…vk} and {w1…wl} are the basis of V belong to Rn, then k = l., and is called dim V, dimensions of V. Why?

Since w vectors live in the same space Rn composed of v vectors, we can try to express w vectors(left) using the composition of v vectors(Right, apply column operation)