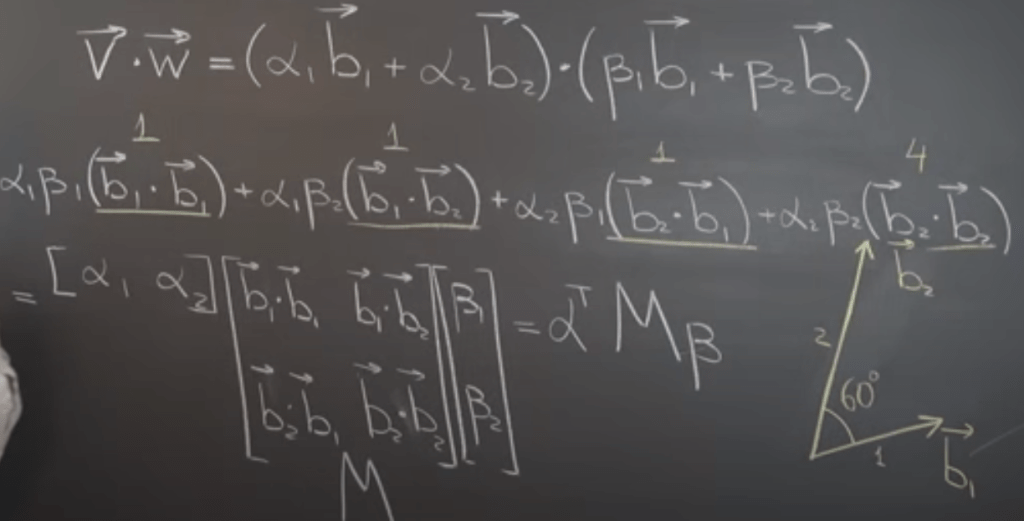Length preserving transformation Q satisfies below equation, hence QtQ=I, it’s called orthogonal matrices.

What can infer from above is

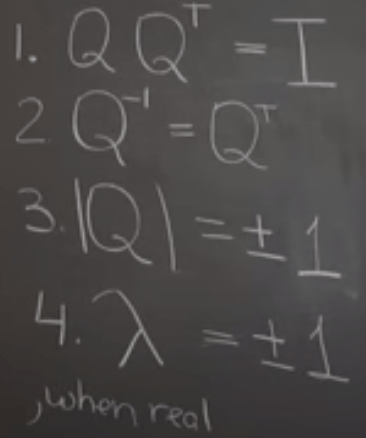
What is orthogonal matrix? Orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. One way to express this is Q^{\mathrm {T} }Q=QQ^{\mathrm {T} }=I, where Qᵀ is the transpose of Q and I is the identity matrix. Then we provide proof that Length Preservation Is Itself an Orthogonal Matrix.

Dot product, it’s scaler function. it’s definition is

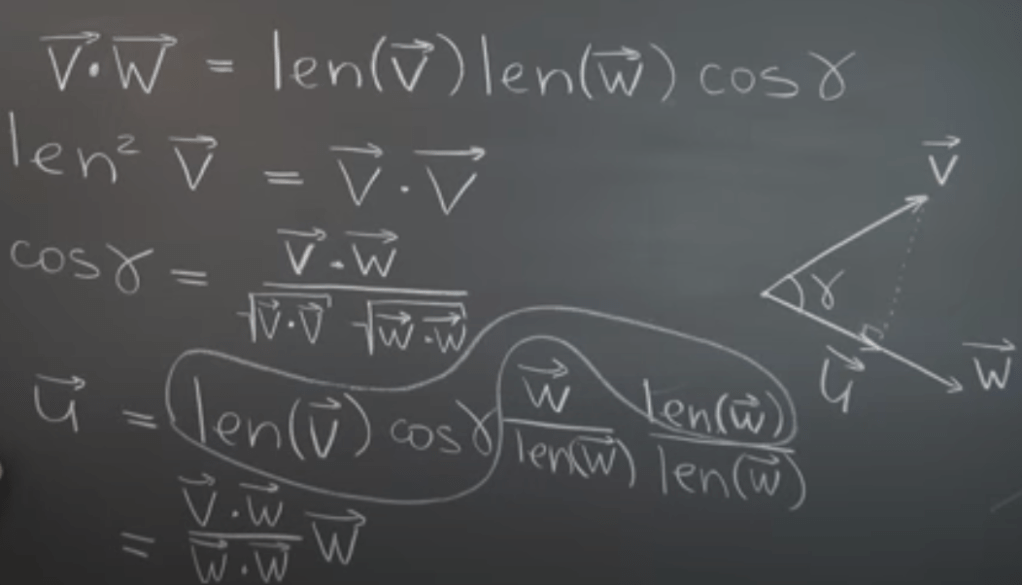
There are three key properties of dot product: commutativity, associativity, and distributivity.

Component Representation of the Dot Product in Cartesian system.

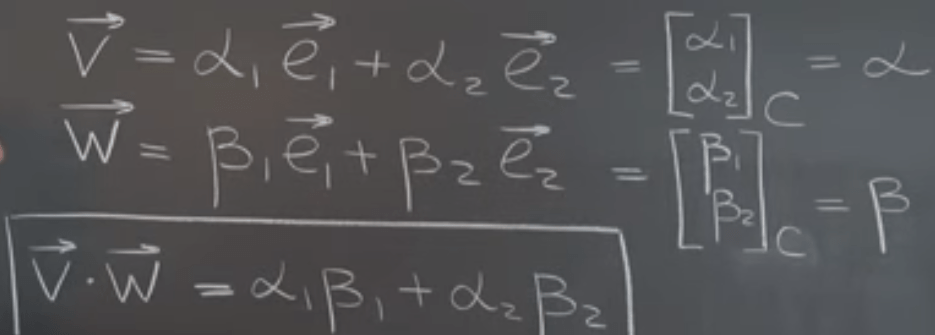
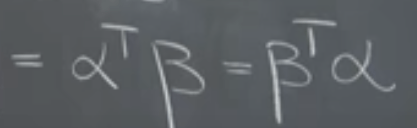
The Dot Product, Matrix Multiplication, and the Magic of Orthogonal Matrices; orthonormal columns implies orthonormal rows. Note if columns are orthogonal only rows are nothing special. only when it’s orthonormal rows and columns share the same property.

If the basis system is not cartesian, say a vector and b vector with some non-90 degree angle in between: