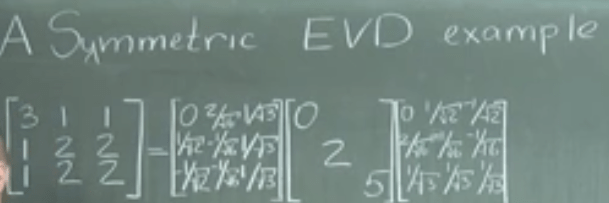Following the previous blog about Gram-Schmidt orthogonal basis computation and we know the Legendre polynomials are superior than the set of terms we intuitively conjured up, it’s time to tap on the glorious Gaussian Quadrature.

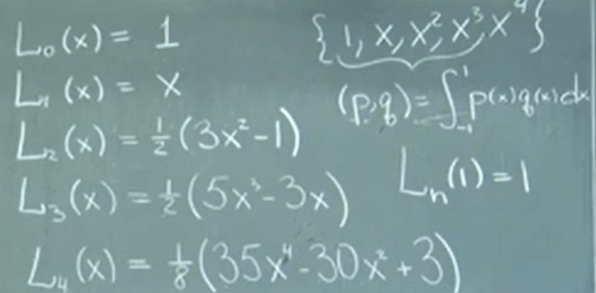
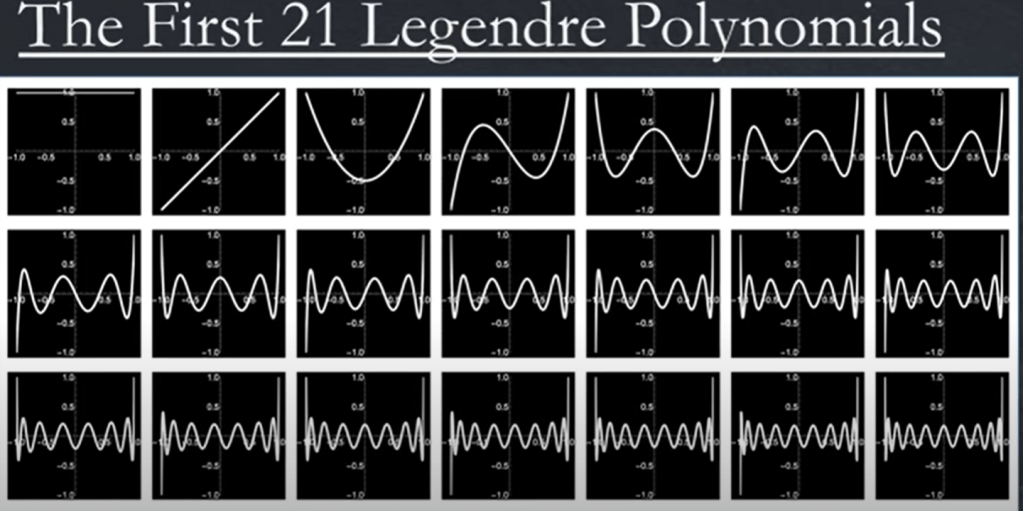
The ingenuous thought is that any function can be regarded as synthetization of an array of component functions(orthogonal basis polynomials). So this Gaussian Quadrature idea of breaking down into component function with various weights to approximate any complex functions is clever but pragmatically not as effective as just perform a trepoz integral. The detailed explanation of Gaussian Quadrature is going to be visited later on.

Generally any inner product can be represented in matrix, however, does an arbitrary form qualifies as “inner product”, meaning pass these three pillars:

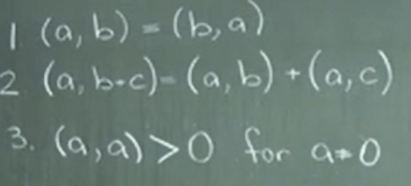
for example

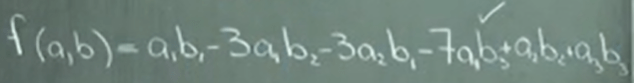
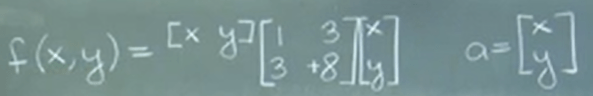
 A matrix is singular iff its determinant is 0, singular matrix has linear dependency in between or co-planer.

BᵀMB Always Positive Definite.

first we prove that this is symmetric as M too

Symmetric matrix has the property that  LDU and LDLᵀ are equivalent.

Eigenvectors of Symmetric Matrices Are Orthogonal. It’s easy to prove the case when they have distinctive eigen values

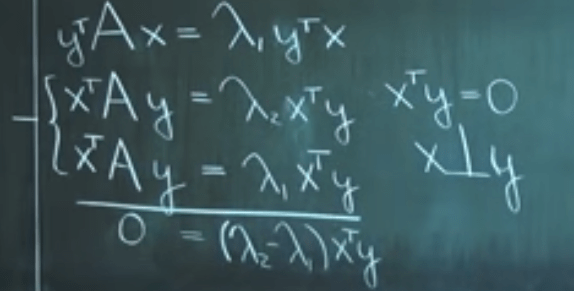
As a result, for any symmetric A, we can get the decomposition as XlambdaXt, do some example cases: