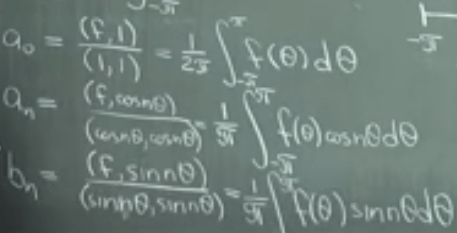Edit on April 02, 2022 where the least square approximation is better clarified by dr. Trefor.

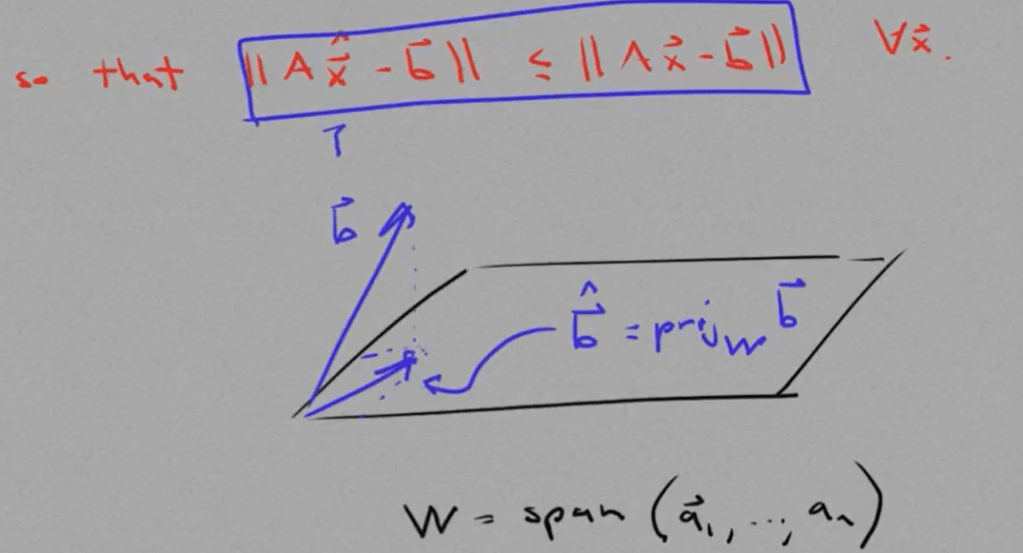
In real life, we constantly need to solve problem Ax=b, but often time there is no unique solution x to get b, the reason is that b vector live in a space above(greater) than the column space w composed of columns a1 to an.

So we don’t give up, want to find the approximation to b, that x hat leads to. this x hat could be our best APPROXIMATE solution given no solution exists.

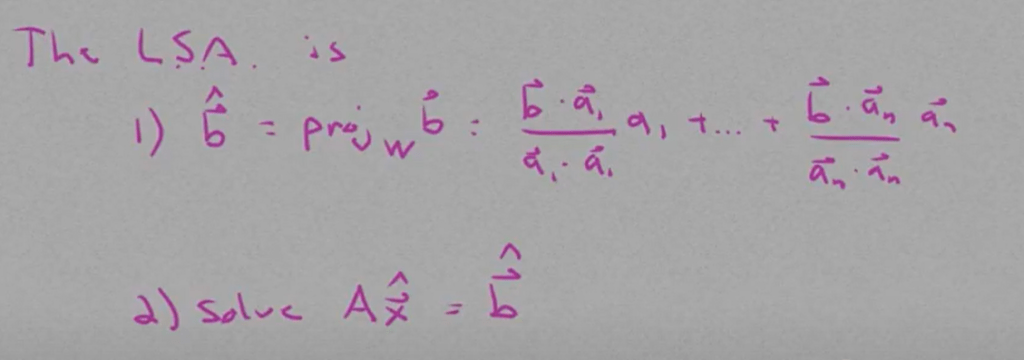
after solve this system equation, the x hat is our solution.

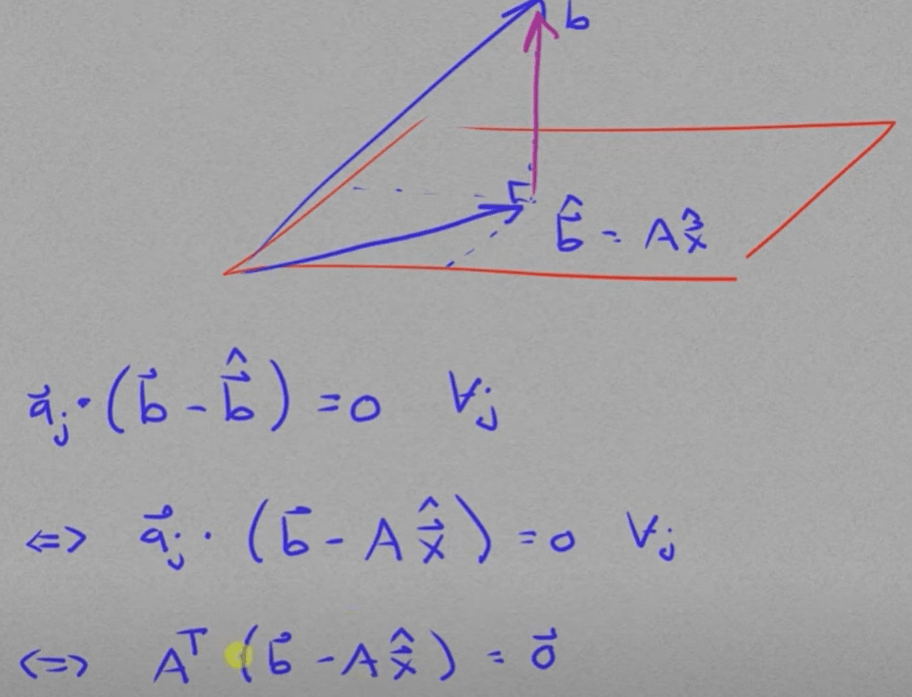
Key note here the column space is composed of aj vector, columns a1 to an, it is exactly the transpose of matrix A composed of rows. Then the problem is simplified more to be

Further digging, why aj set = A^T? It should come intuitively for LA learners that “row space of a matrix equal to the column space of the transpose of matrix“.

Decomposition by inner product with general basis not orthonormal basis is like

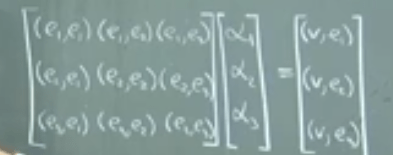
Now let’s tackle Fourier series, where any function(theta) within a range from -pie to pie; later on we know this range limit can be loosen up to infinite scope.

Trying to decompose it into “finite” basis terms:

To find the coefficient a0, an and bn, we need to have f(theta) to dot the basis function g to get the length, this length is the coefficient. Because in orthogonal base system,