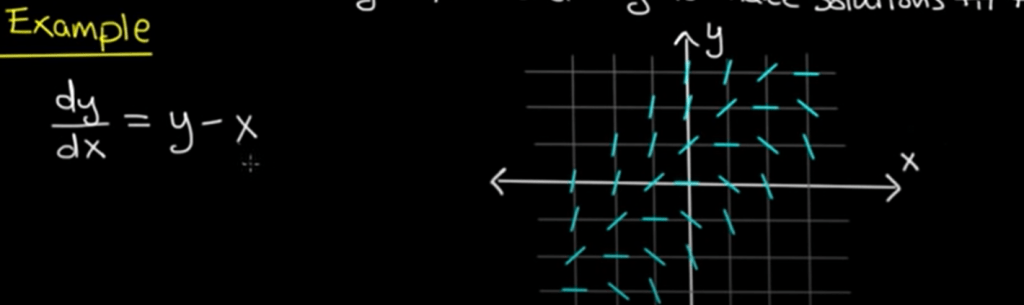
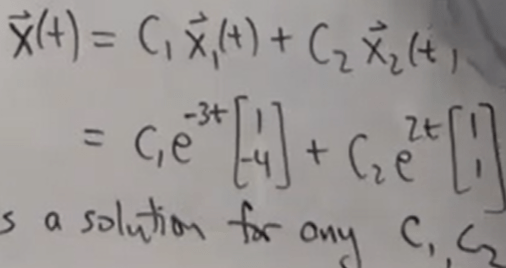Skipping through basic known facts about ODE, let’s jump into something bit of novice: slope fields. Why called slope? because dy/dx is the derivative also is the slope geometrically.

For example what is the picture of dy/dx=y-x
To solve ODE, Separating variables is very powerful technique. dy/dx=g(x)/g(y). For example,
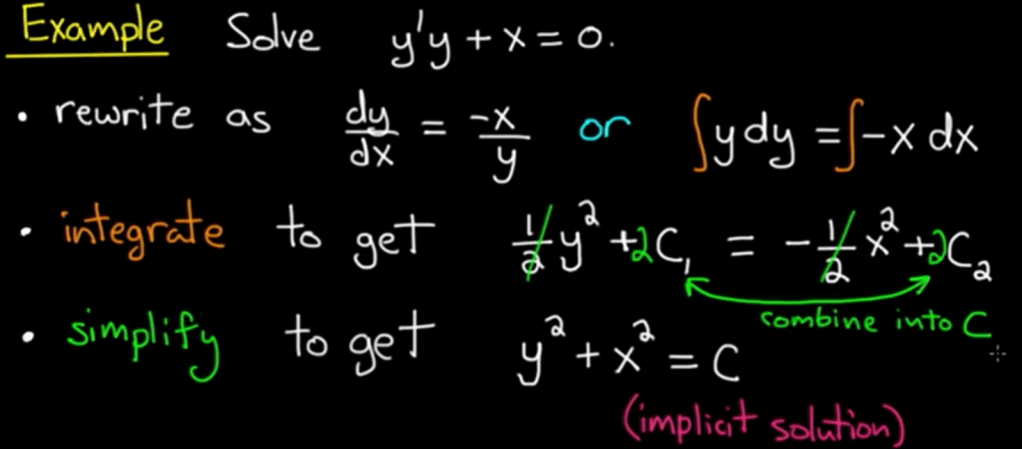
Integrating Factors: it’s a very useful tool to solve linear ODE for example in the below equation to solve, if we can spot the left part is the derivative of xy, then it’s very easy to solve as shown below
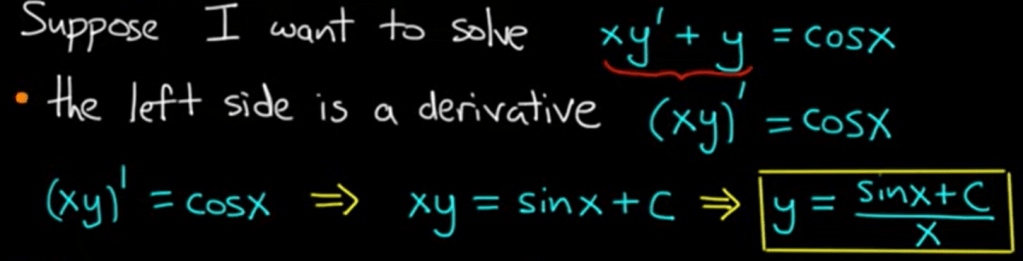
Given this example, we can try to multiply an integrating factor to make it a derivative, so the problem becomes solvable. The generic steps are

Grasping this first order ODE technique is to solve real world problem such as this water filling in tank

Population model is another classical example of ODE application

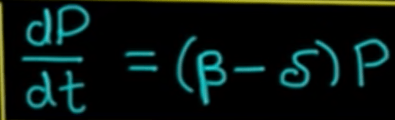
Phase Diagram is a way to visualize autonomous ODE

such as
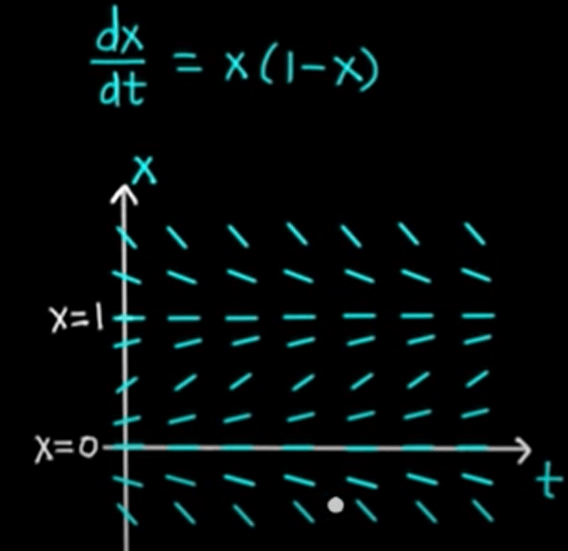
So we can see depending where the position is, there is the tendency/trend to move away(unstable), toward, or non-moving(equilibrium) state.
An interesting question to ask is that given the phase line, can we deduce what the ODE equation is?

It’s easy, plot it by thinking about the slope and connect the dots
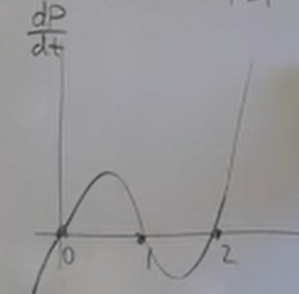
The equation should be
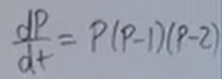
Bifurcation diagrams to study how an ODE depends on a parameter. For example the population growth model with the harvesting variable h:

if we just observe x and h relationship(Below), it’s a hyperbola curve

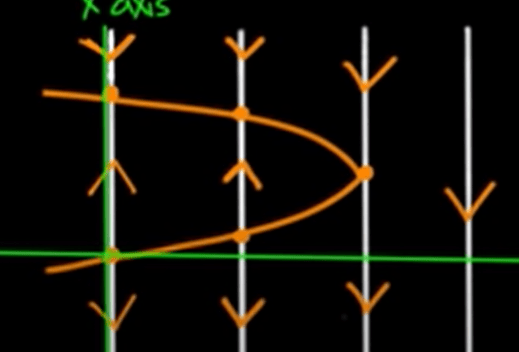
It visually answers the question the maximum harvesting amount people can do in a year without killing the whole fish population.
Next Principle of superposition is a profoundly important concept in linear algebra.

So here is the proof:
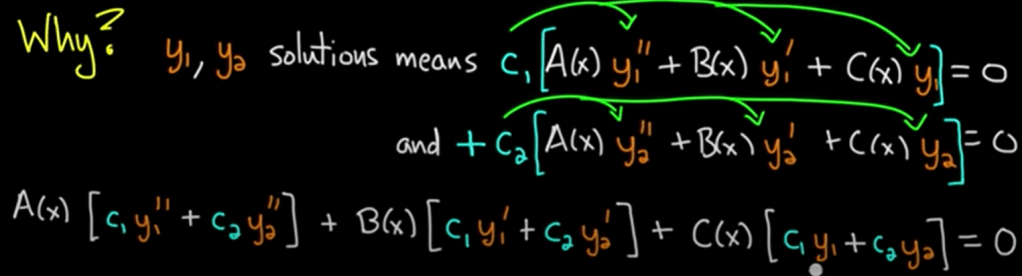

Now let’s look into a classical example
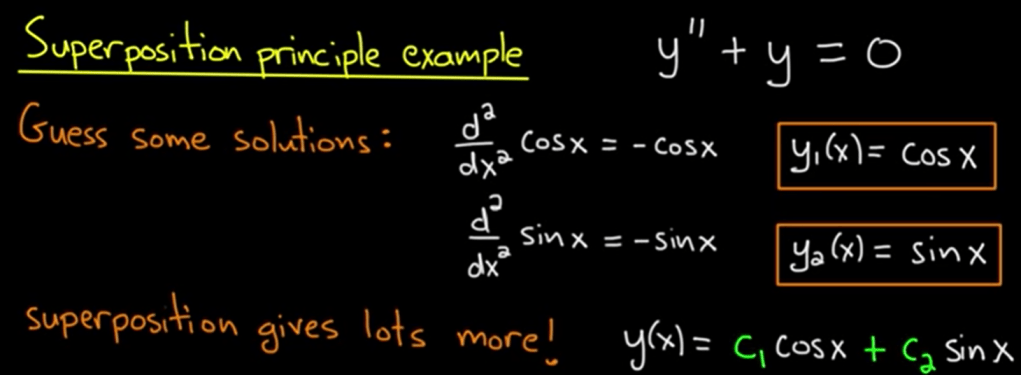
If add the IVP condition
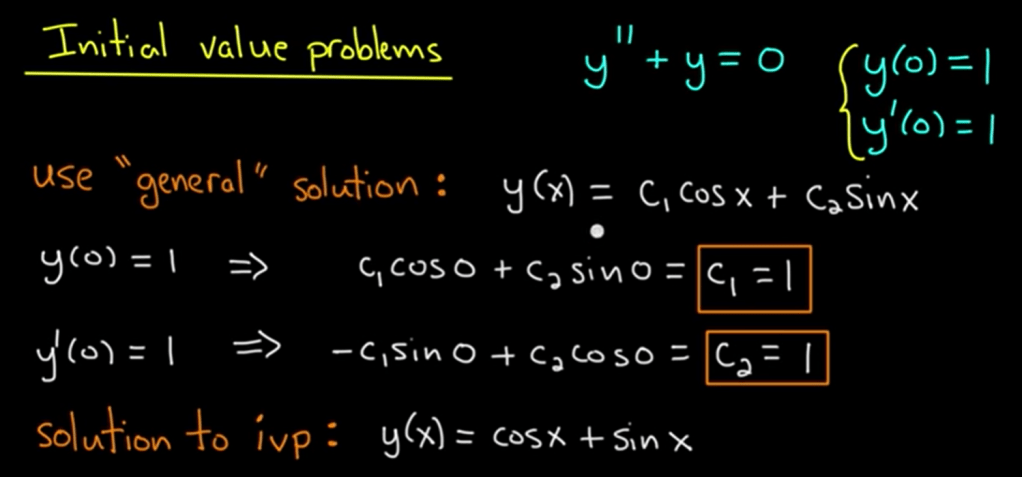
Any of these higher order ODE equation problem, we should apply the linear algebra mindset to see it’s actually just to find a particular solution plus null space. If it’s not homogeneous, try to find the particular solution to exact that output, the rest, finding null space is same as solving homogeneous problem.
What if the roots are repeated, that means the null space doesn’t have the sufficient number of null terms. It will break in the end for example:
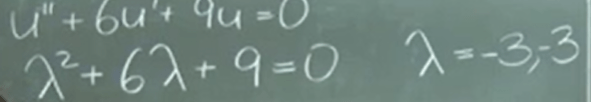
Adding a t in front of the exponential solution term is a way
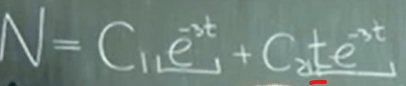
It is a generic recipe, so now we go back to try the simplest ODE, we can get the right answer:

Next, to study the 2D linear system

It can be written in this succinct matrix form as per LA knowledge
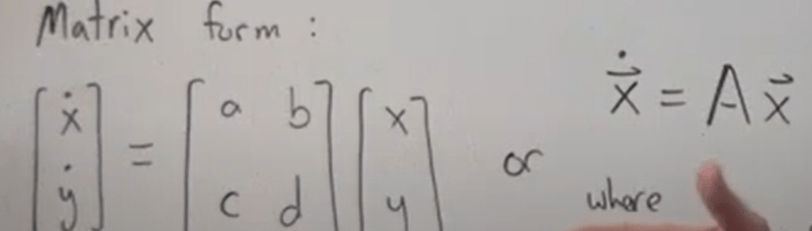
Here is a simple example

if a = -1, the situation is pictured as

If a = -2, the decay happened on x axis more quickly than on y

if a = 1

What if the 2D linear system problem is normal, not decoupled? for example

The solution is from ingenious guess of a straight line solution might look like e raised to lambda t times the vector v.
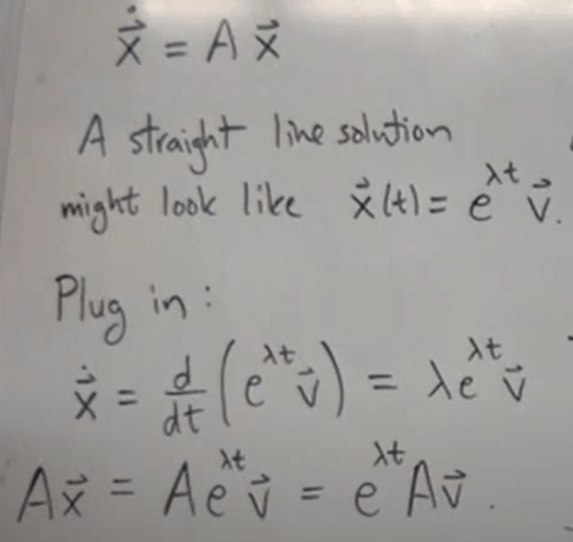
Then the inference
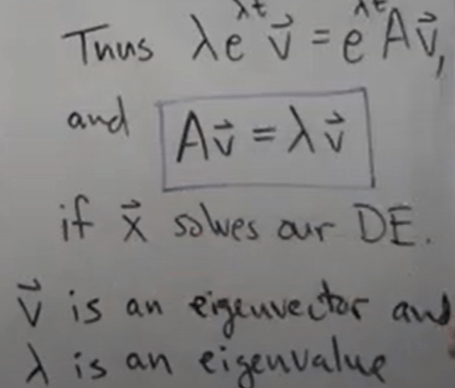
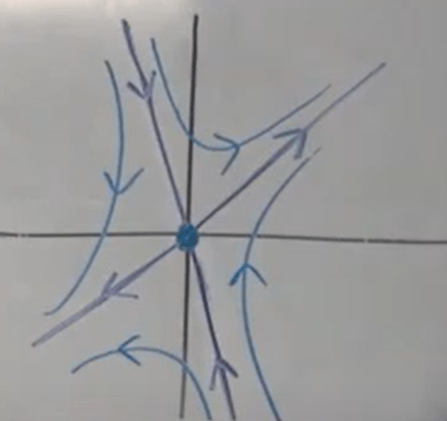
The general solution is