PDE is much harder than ODE. let’s start from the comparison between ODE and PDE. It’s from commutant, I stopped at the decayed transport equation.

The form of PDE is quite similar except that the right part of the equation U is dependent on more than one variable t:

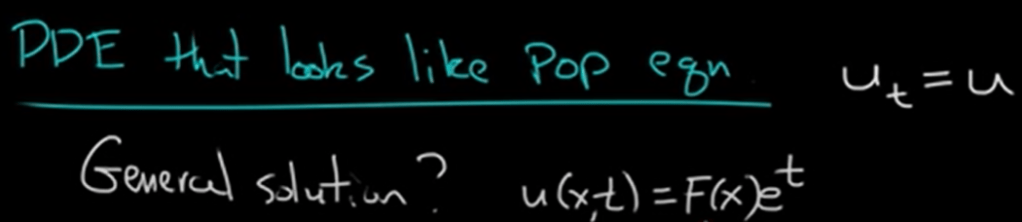
There are three types of PDEs

Another perspective to categorize PDEs is from khan of faculty

There are three major steps in PDEs, 1. formulate PDE from the phenomena; 2. solve the equation; 3. interpret the equation.

For example, the wave transport equation is not easy to formulate:

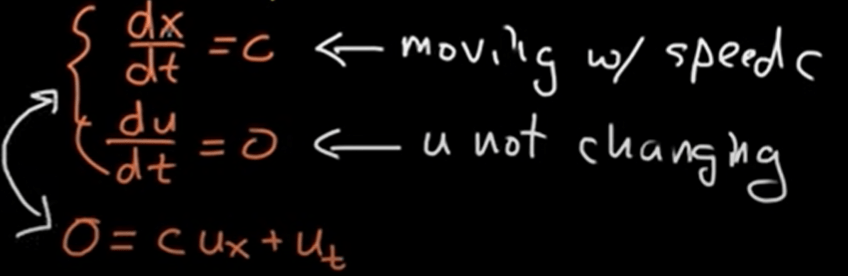
To solve this wave transport PDE problem, a moving(at speed c) coordinate system is introduced.

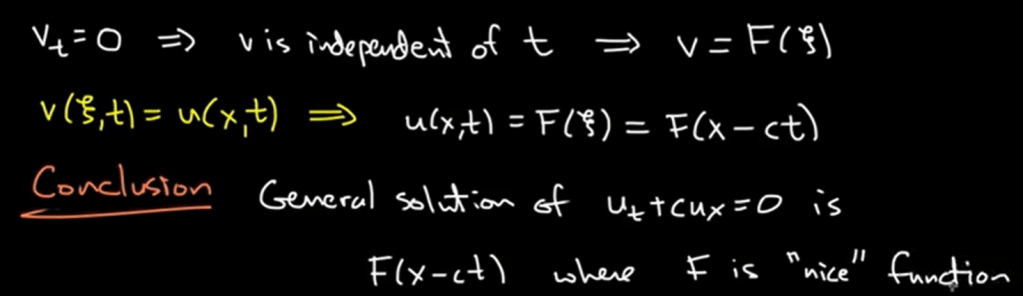
Then “Method of characteristics” is applied to reduce the PDE to ODE.

For heat equation, parabolic type of PDE, a classical solution to the 1-D Heat/Diffusion PDE is by Separation of Variables. Generalizing, suppose the PDE comes with the following Boundary Conditions and Initial Conditions:

U(x, t) can be expressed as X(t)T(t), since it’s linear, it can be expressed as infinitely many such solutions in summation:

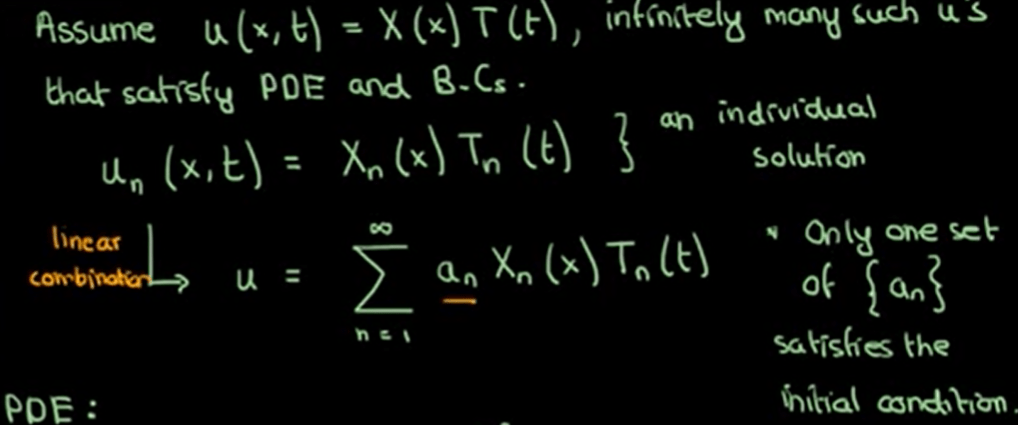
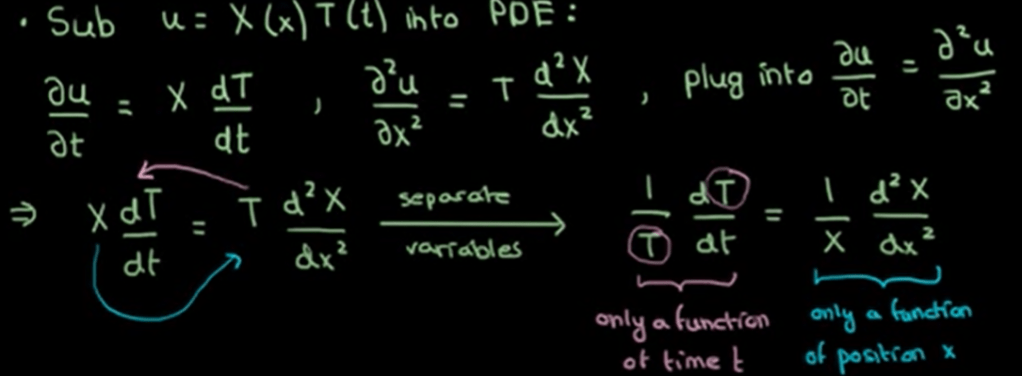
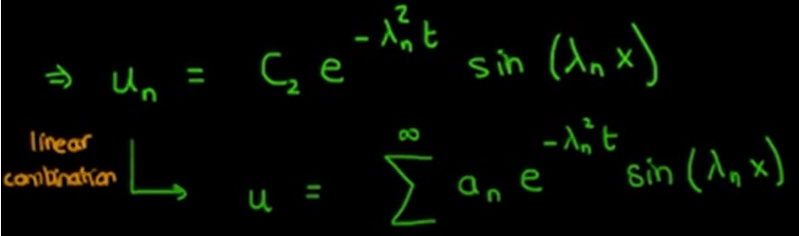
Next, Sturm-Liouville Equation is applied, so it’s necessary to dig separately what it is. (Sturm-Liouville problem, or eigenvalue problem, in mathematics, a certain class of partial differential equations (PDEs) subject to extra constraints, known as boundary values, on the solutions. Such equations are common in both classical physics (e.g., thermal conduction) and quantum mechanics (e.g., Schrödinger equation) to describe processes where some external value (boundary value) is held constant while the system of interest transmits some form of energy.)

(need to add later the intermediate steps in arriving to the conclusion below