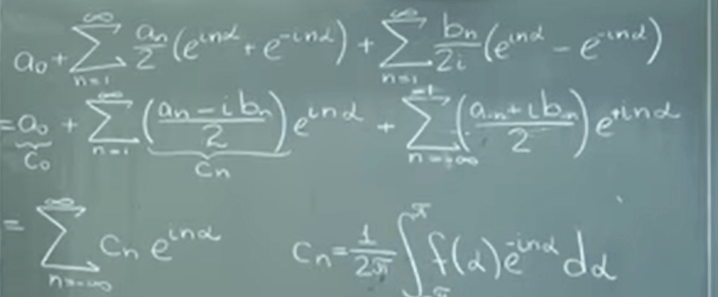ODE of such will lead to problems because when lambda = 4, the part on the right side of the equation is also in null space.

If we try this solution (adding t in front of the exponential term), it works

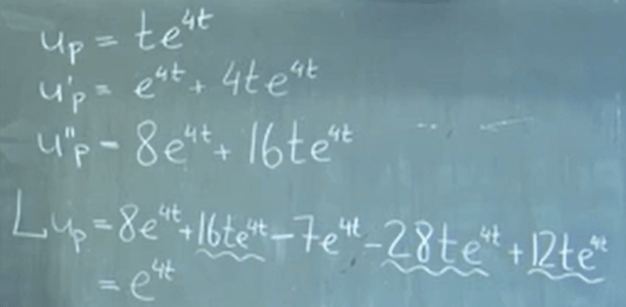
This simple example help to introduce a very important concept in our world – Resonance.

Further understand Resonance, here is a classical resonance formula

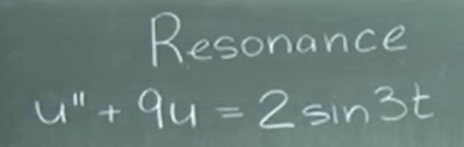
Guess u = tsin3t leads to cosine at left side, so then we try u = tcos3t, which has a valid output

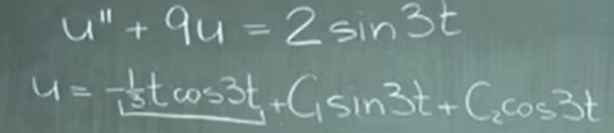
… can add the interim knowledge later on

Moving on the PDE, starting from the basic forms and basic approach – separate variables.

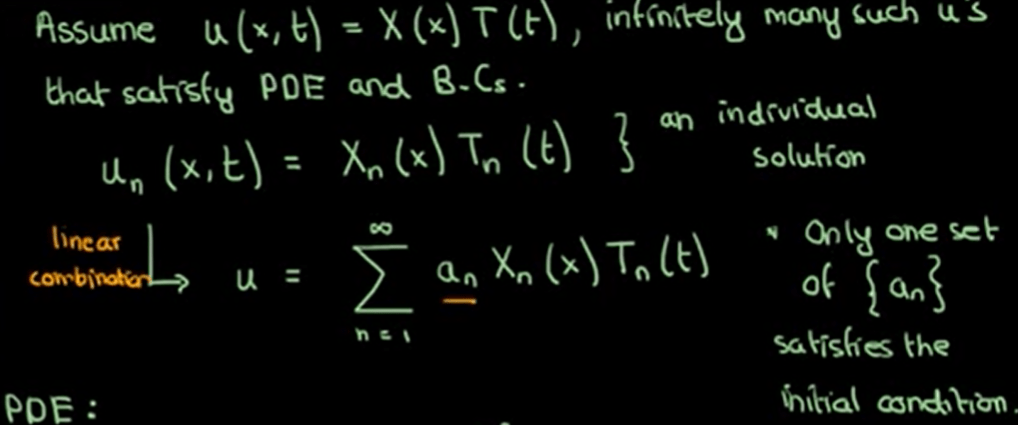
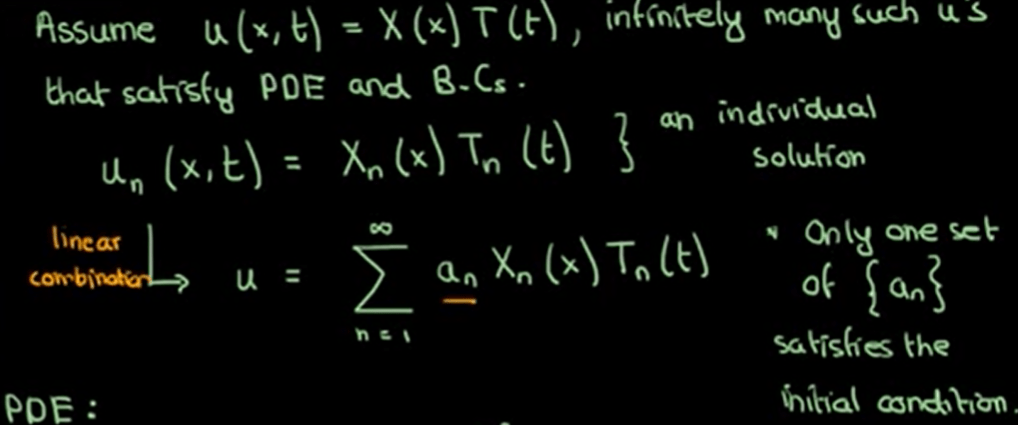
From Dr.Grinfeld’s lecture, it is

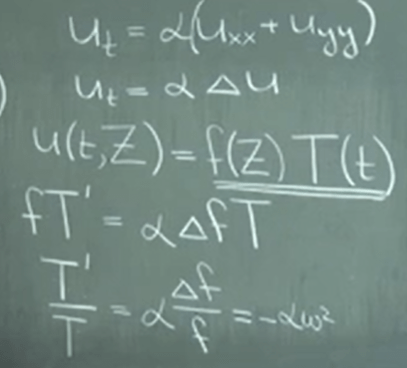
Then the final formula for u(t, Z) = f(Z)T(t) is as below per linear property

Above lay out the equation for one order on time t equation (heat equation), let’s now look at wave equation – order two time t equation

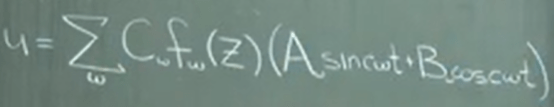
To make the formula look more compact, assume

so Asincwt + Bcoscwt can be written as

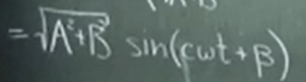
It sets the prelude to Fourier Series. In LA, it is revealed that FS is nothing abut a least square (approximating) problem. if n can go infinite, then it’s not a typical least square approximation r = Ax – b (matrix format), it’s precise.

It’s so powerful because it’s to solve very universal function f(Z)! Adding the Laplace operator in front, making it broken down to infinite number of sin and cos combinations.

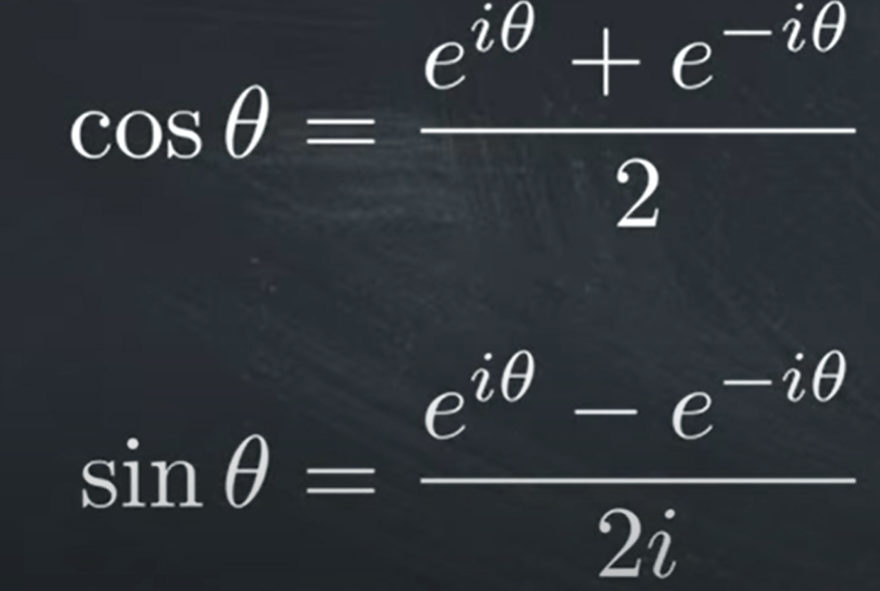
The complex form of Fourier Series can be written from

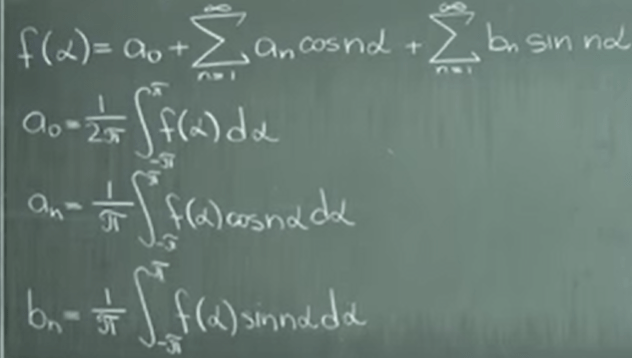
to