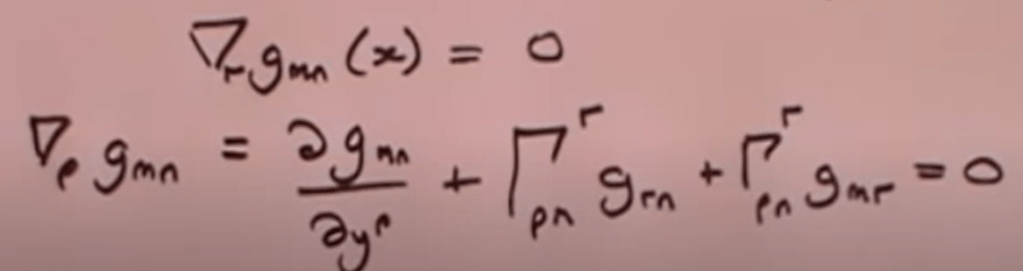It’s the first attempt to understand Einstein’s Field Equations. Thanks to DrphysicsA.

It starts with the famous Einstein “equivalence” premise that there is no way one can tell the difference between a gravitation field near a mass and an accelerating spaceship. a light traveling straight in an uplifting spaceship looks like being bended, hence, we will observe on earth bended light phenomena too. Einstein’s theory was proved by viewing the hidden star as shown below.

Here is the field equation

The left side of the equation is the description of space curvature, right side refers to the mass and energy. Hence it is said as “Mass tells spacetime how to curve and curved spacetime tells mass how to move”. To grasp the equation, we need to know Metric tensor, Christoffel symbol gamma, Ricci tensor, curvature scalar, stress energy momentum tensor, cosmological constant.

Breaking them down to first explain metric tensor. Metric tensor essentially is to convert between various coordinate systems.

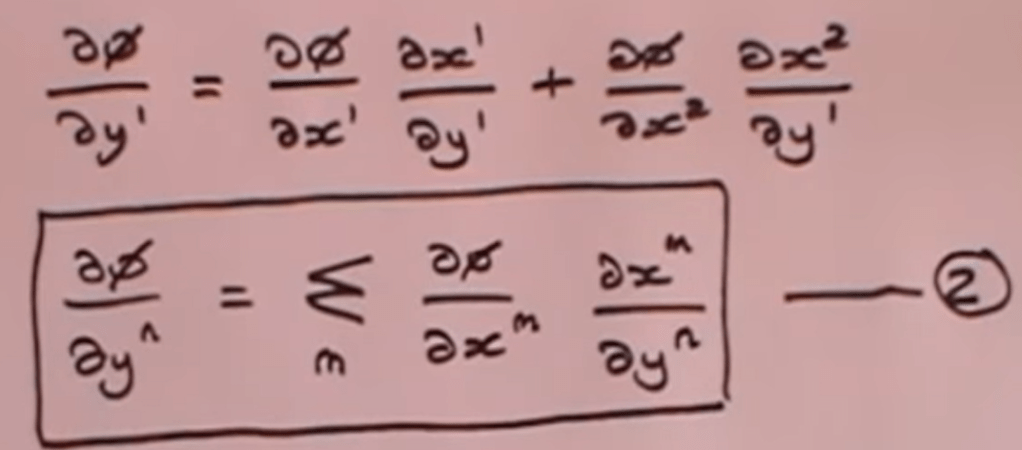
Replace the left side and end right side with vector (first derivative), here is the nth vector in y coordinate expressed by x coordinates all dimensions.

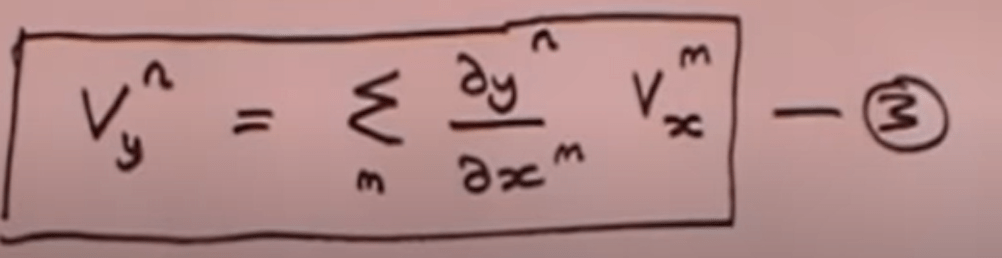
Once we know how a single vector in y system is expressed in x coordinates, now in physics, taking the most simple scenario – exerting a force on an object on the floor and do the work of moving it for some distance, F and distance are both vectors. work done = F*cosalpha*S, so we need to introduce this concept of tensor

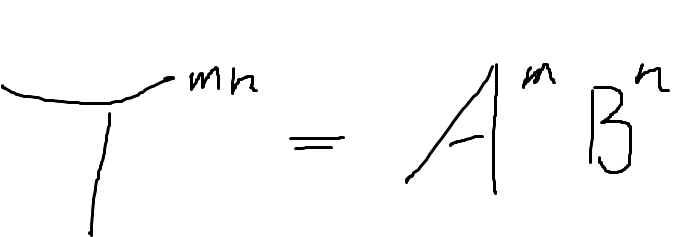
So we can easily deduce the contravariant transformation.

Correspondingly, there is the covariant transformation

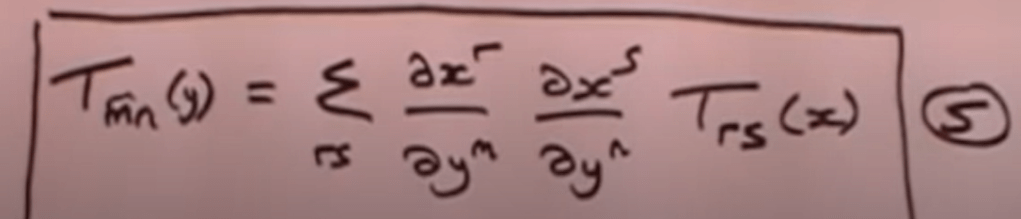
Now in order to “expand pythagonal equation in all coordinate systems, doesn’t have to be orthogonal …), DrphysicsA manipulate expression as

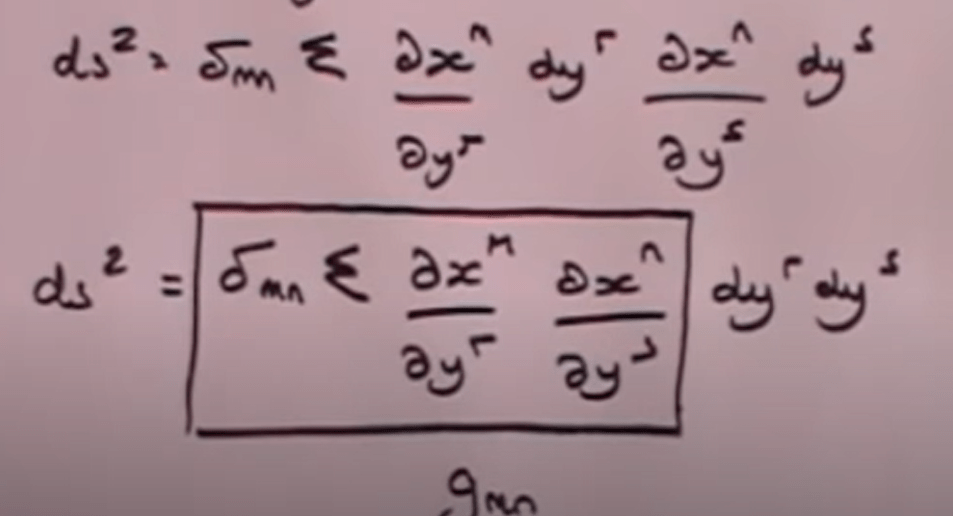
Note here he just manipulated the formula in multiple coordinate systems conversions to reach metric tensor gmn, comparing to the classical way – tensor calculus way:

Next we proceed to Christoffel Symbol. The profound question to ask here is that if there is a tensor T in x coordinate system, it must be same T in y coordinate systems. However, whether their derivatives are same? unfortunately, they are not, there is an additional part – christoffel symbol.

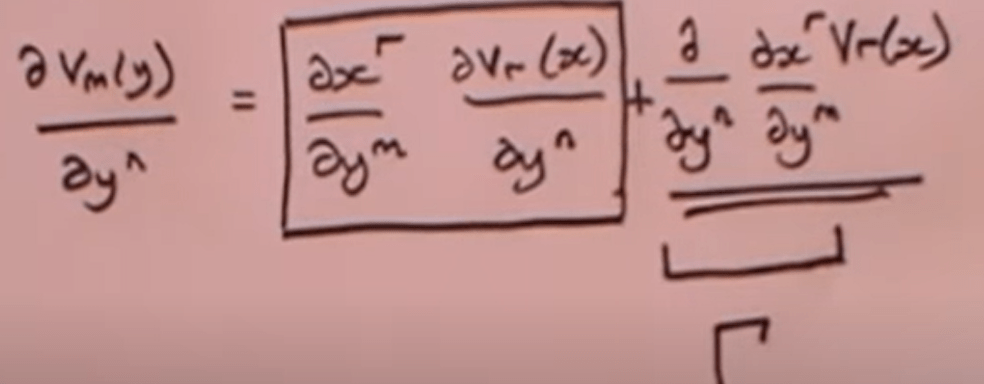
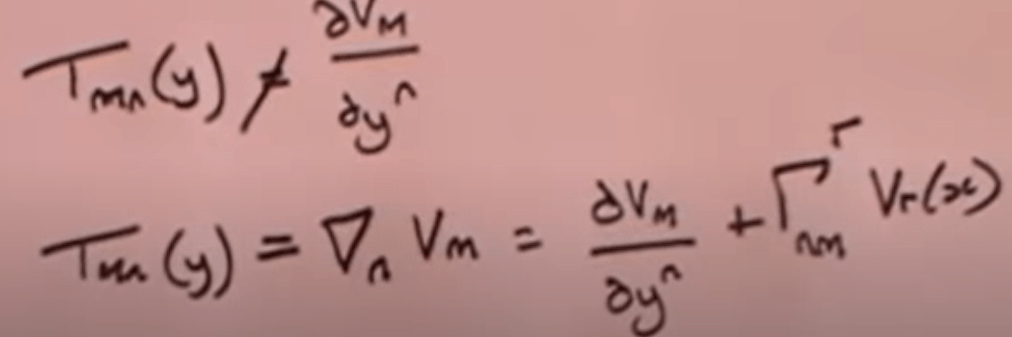
Comparing the classical lecture by Dr.Grenfeld:

Dr.Grinfeld’s Tensor Calculus has detailed the notion of Christoffel symbol in unique way, thinking about the Christoffel symbol is the component or coefficient of the vector in the left side expressed by component times the base vector.

It can be converted to this too

Using a polar coordinate system as an example to further illustrate

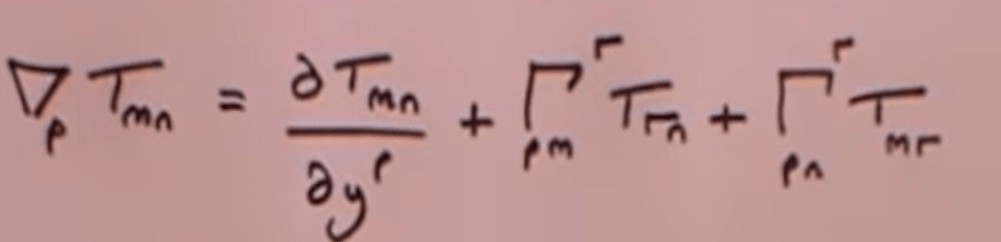
Now if we plug in gmn as Tmn,