There are four types of definitions: flat space, extrinsic for curved space, intrinsic for curved space and abstract definition, which is a directional derivative.

In a flat space,

Christoffel symbol part is zero in flat space cartesian coordinate system, but in polar coordinate it’s different. First, the right way to interpret the Christoffel symbols is Christoffel part is the component, hence the following expression holds:

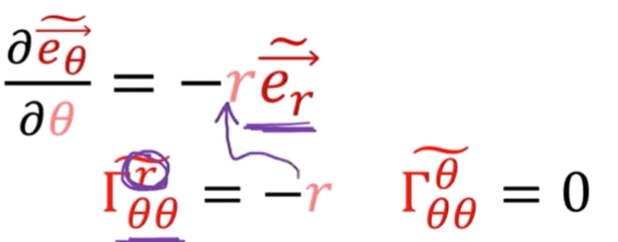
There are some notational difference between engineer and math fellows. Engineers like matrix form:

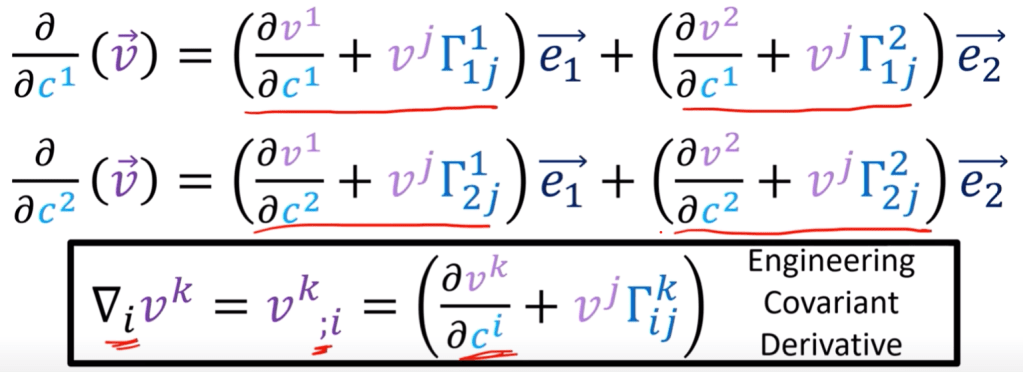
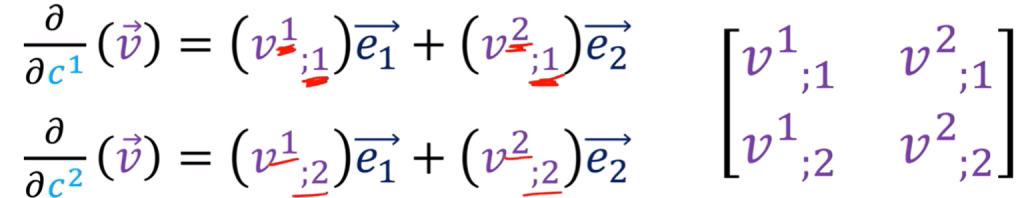
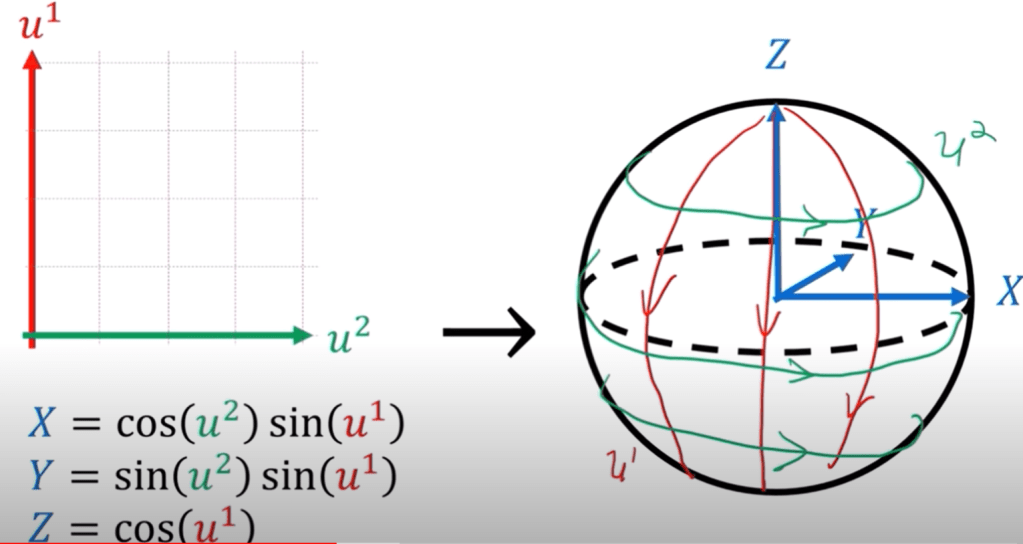
In a curved space, from an extrinsic view(bird’s eye view):

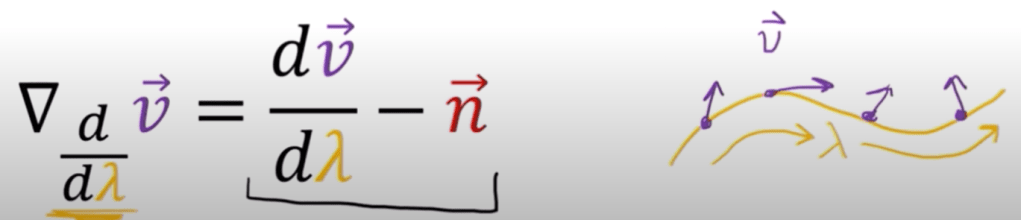
It is actually consistent with the definition in flat space where the normal vector part is zero vector, hence dismissed. Also worth noting is the comparison to gradient like a hill, directional derivative(here is covariant derivative) the expression is same, but there is no notion of normal vector needed. Because under that scenario, we only process flat space too.

When it is zero vector the vector v is parallel transport in the direction of w vector. Take an example of parallel transport on a sphere with radius 1.

Skipping the middle steps we get

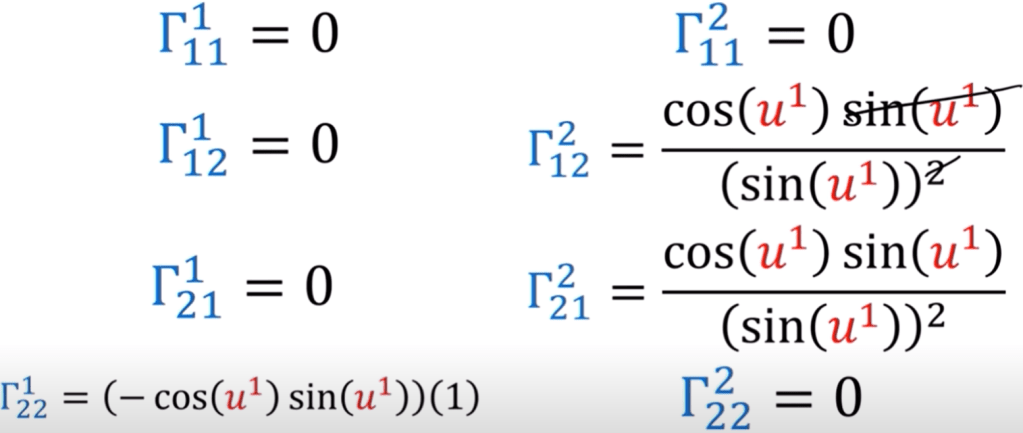
So if the path is indicated by the lambda(yellow) parametrization here and assume there is this vector(purple) equation as below

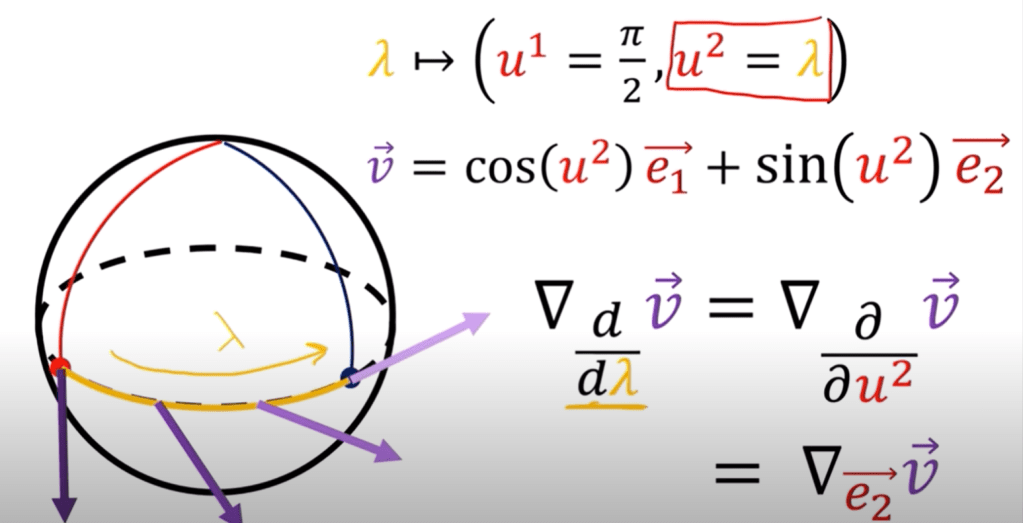
After calculation, we get a non-zero covariant below, hence this purple vector is not doing a parallel transport.

Alternatively, if the vector we give is

It makes sense that this vector field on directional (covariant derivative) doesn’t have tangent part. hence it’s parallel transport.

Reversely, if we start with a rule to always do “parallel transport” then apply the math to find the vector path/equation.

Another more complex example is not to move along the equator but upper part where the latitude is pie over 4.

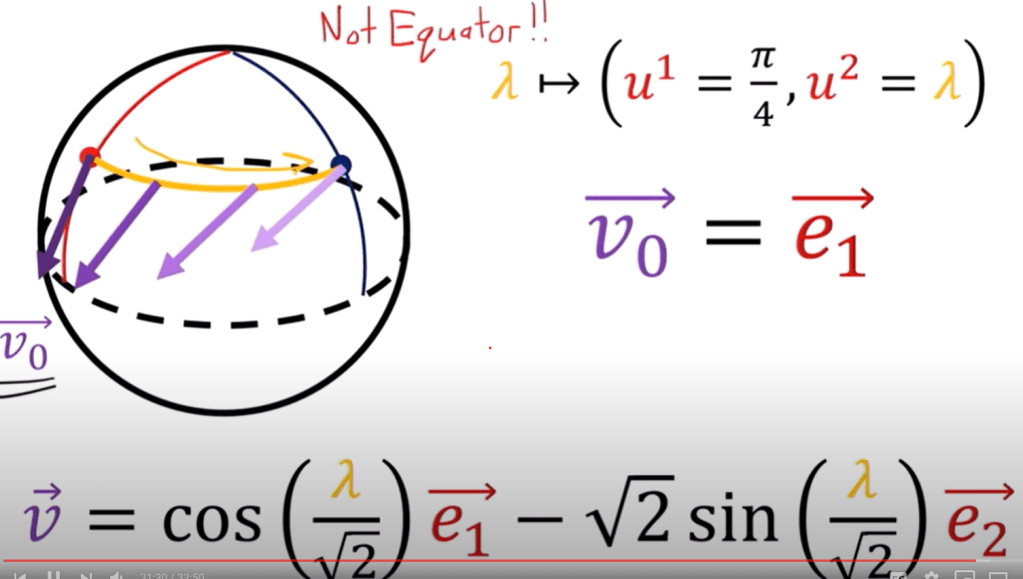
Now still in a curved space or manifold, taking an intrinsic view or bug’s eye view. The key difference is that by definition, there can’t be a normal vector part to substract because we can’t have that additional dimension in bug’s world.

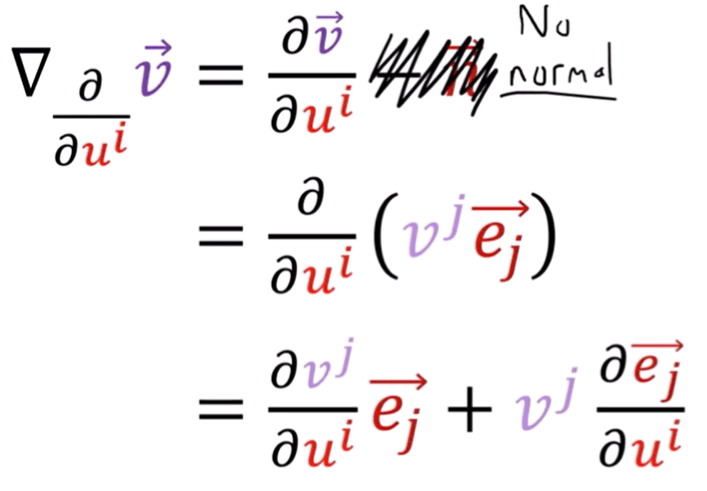
To compute some ingenuity is needed especially on Christoffel symbols,

As a result we have the new math tools:

In summary, without bird’s eye view, to realize geodesic, one needs to do parallel transport, which satisfies the math of covariant derivative is equal to zero vector as below:

Upgrade to abstract definition of covariant derivative because we wil find other covariant derivatives especially the “Levi-Civita connection”, which comes from the fundamental theorem of Riemannian Geometry. Also it extends covariant derivatives to all tensor fields which include not only scalar fields but also vector fields, covector fields and metric tensor fields.

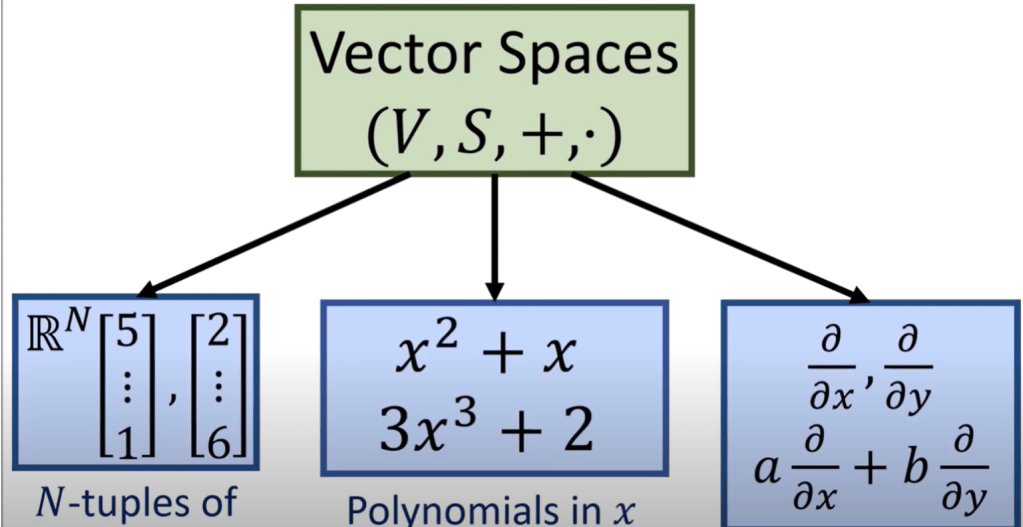
First let’s see how vector space is defined in mathematics to appreciate the power of “abstracting” in math, which, one could say it is the essence and beauty of math.

So back to covariant derivatives, we find they all share these common properties:

Parallel transport provides a connection between tangent spaces in a curved space the math tool – covariant derivative – is also called “connection”. The Christoffel symbols can also be called connection coefficient.

to solve/get the unique “connection coefficient”, we need introduce two more key properties: torsion free property and metric compatibility property.

Torsion is the derivative of curvature, meaning how the underlying space is curved. in defining torsion, we also learn the concept of Lie Bracket or commutator.

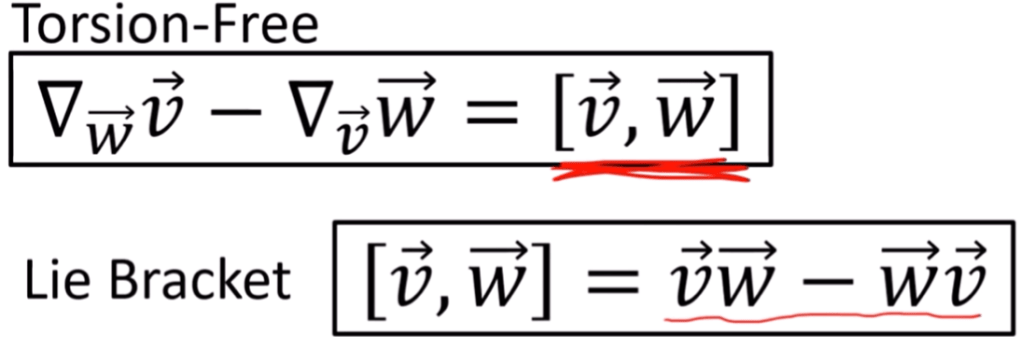
With these two properties and analyze the special case of moving parallel, we get the below christoffel symbol denoting Levi-Civita Connection.

The Levi-Civita Connection is what has been laboriously worked on. Additionally if we let the Christoffel symbol = 0, we get “boring connection”. It is not metric compatible.

Then we can follow the same line of reasoning to get the “covariant derivative of COVECTOR”, to get the “covariant derivative of a Tensor”: